Blender BMesh数据结构解密
Posted 新缸中之脑
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Blender BMesh数据结构解密相关的知识,希望对你有一定的参考价值。
BMesh 是一种非流形边界表示。 它旨在取代当前有限的 EditMesh 结构,解决 EditMesh 的许多设计限制和维护问题。 它与径向边结构相当。

推荐:使用 NSDT场景设计器 快速搭建 可编程 3D场景。
1、BMesh实体
在最基本的层面上,BMesh 将拓扑存储在四个主要元素结构中:
- Faces:面
- Loops:环,存储每个面顶点数据、uvs、vcols 等
- Edges:边
- Verts:顶点
1.1 顶点/Verts
顶点存储坐标并链接到顶点的圆盘循环中的边(下面介绍)。
1.2 边/Edges
边(Edges)表示两个顶点之间的连接,但也存储到边的径向环中的环的链接(在下面介绍)。
1.3环/Loops
环(Loops)定义面的边界环。 每个环在逻辑上对应于一条边,尽管环是局部于单个面的,因此每条边通常会有多个环(表面的边界边除外)。
环存储几个方便的指针:
- e - 指向环的边的指针
- v - 指向边起始顶点的指针(其中“起点”由 CCW 顺序定义)
- f - 指向与此环关联的面的指针。
环存储每个面的顶点数据(以及本文档后面概述的其他内容)。
1.4 面/Faces
面链接到一个环,环的循环链表定义了面的边界。
1.5 持久标志
网格中的每个元素(顶点/边/环/面)都有一个关联的持久位域,这些标志存储信息,例如实体的可见性或其选中状态。
2、连接循环
BMesh结构具有以下特点:
- 持久邻接信息
- 本地可修改拓扑
- 任意边数的面 (N-Gons)
- 表示任何非流形条件,包括线边缘。
第二个到第四个特征都依赖于第一个,因此提供此功能的系统是 bmesh 数据结构的基础。 持久邻接信息使用双向循环链表系统存储,该系统维护拓扑实体之间的关系。 这些链表在概念上与其他边界表示(例如半边、径向边和部分实体)中的链表相同,并且与这些其他表示一样,每个拓扑实体本身就是它所属的循环中的一个节点,因此存储邻接的内存要求 信息仍然很少。
元素之间的连接由围绕拓扑实体的环(Loops)定义,称为循环(Cycles)。 每个循环的基础是循环被设计用来回答邻接查询的实体。 例如,一个旨在回答“哪些边共享该顶点”问题的循环会将顶点本身作为基础,将边作为循环的节点。 请注意,不需要显式存储所有可能的邻接关系,并且可以通过结合使用两个或多个循环来快速导出完整的连接信息。
bmesh 结构中显式存储的三个循环是圆盘循环(Disk Cycles)、径向循环(Radial Cycles)和环循环(Loop Cycles)。 下面概述了每个循环的属性和处理它们的函数列表。 请务必注意,标有星号 (*) 的函数不是 Mesh Tools API 的一部分,仅供建模内核使用。 此外,当列出结构定义时,为了清楚起见,它们省略了某些成员。
2.1 圆盘循环/Disk Cycle
圆盘循环是围绕一个顶点的一圈边。
基础: BM_EDGE_DISK_LINK_GET(BMEdge *,BMVert *)

圆盘循环在结构上是最复杂的。 每个 BMEdge 包含两个 BMDiskLink 结构,用于跟踪该边在其每个顶点的圆盘循环中的成员资格(顶点 v1 为 v1_disk_link,顶点 v2 为 v2_disk_link2)。 然而,对于任何给定的顶点,它可能由其圆盘循环中某些边中的 v1 指针和其他边中的 v2 指针表示。 bmesh_disk_ 系列函数包含一些用于导航圆盘循环的实用工具,并向网格工具作者隐藏了此细节。 请注意,与半边结构不同,圆盘周期完全独立于面数据。 这样做的一个优点是线边缘完全集成到拓扑数据库中。 另一个是圆盘循环在处理涉及面的非流形条件时没有问题。
与圆盘循环相关的函数:
- bmesh_disk_edge_append
- bmesh_disk_edge_remove
- bmesh_disk_edge_next
2.2 环循环/Loop Cycle
环循环是围绕多边形面的边的表示。
基础: BM_FACE_FIRST_LOOP(BMFace *)
要了解环循环,必须了解多边形在 bmesh 建模器中的存储方式。 每个面都由以下两个结构表示:
typedef struct BMFace
BMHeader head;
struct BMFlagLayer *oflags; /* an array of flags, mostly used by the operator stack */
int len; /*includes all boundary loops*/
BMLoop *l_first;
float no[3];
short mat_nr;
BMFace;
typedef struct BMLoop
BMHeader head;
/* notice no flags layer */
struct BMVert *v;
struct BMEdge *e; /* edge, using verts (v, next->v) */
struct BMFace *f;
/* --- snip --- */
BMLoop;
BMFace 结构是存储在 BMesh 结构中的 ListBase 的一部分。 它不显式存储与其关联的顶点或边。 相反,它只是存储一个指向面的环循环中第一个 BMLoop 的指针。 下图显示了 BMLoops 在顺时针绕组面中的排列。

从图中可以看出,BMLoop结构类似于half-edge,它是按照面绕向的,只存储一个顶点的引用。 因为每个循环也与一个 BMEdge 相关联,所以循环的一个必须成立的属性是 loop->v 和 loop->next->v 必须都包含在 loop->e 中。 无论如何,循环的顶点指针与面对齐,而不是边对齐,多边形中的第一个顶点将始终为 face->loopbase->v 而第二个将是 face->loopbase->next->v 。
与环循环相关的函数:
- bmesh_cycle_* 系列函数。
2.3 径向循环/Radial Cycle
径向循环记录围绕边的一组面。
基础: BMEdge->loop->radial structure
径向循环类似于径向边数据结构中的径向循环。 然而,与径向边不同,bmesh 中的径向循环不需要大量内存来表示非流形条件,因为 bmesh 不跟踪区域或壳信息。

上图说明了径向循环的结构。 虽然任意数量的面,可以与任何给定的边相关联,但每个 BMEdge 存储一个指针,仅指向它的 BMLoops 之一。 这个 BMLoop 被认为是这个 BMEdge 径向循环的基础,通过跟踪每个 BMLoop 结构的径向成员中的 next 和 prev 指针,我们能够访问与特定边相关联的每个面。
与径向循环相关的函数:
- bmesh_radial_append*
- bmesh_radial_loop_remove*
- bmesh_radial_loop_next
- bmesh_radial_face_find
2.4 循环中元素的顺序
请注意,圆盘循环中边的顺序和径向循环中面的顺序是未定义的。 这导致用于导出某些邻接关系的搜索时间略有增加。 然而,优点是网格的固有属性不依赖于循环顺序,并且所有非流形条件都被简单地表示。
2.5 总结
这张图片在一张图片中显示了所有循环,总结了上述部分:

网格编辑 API 可以非正式地分为三层:底层 API,用于遍历 BMesh 循环和进行原始本地编辑;中级 API,以此为基础,提供迭代器、遍历器和更高级别的网格编辑功能;顶层 API,建立在这些层之上,由运算符和编辑工具组成。
3、BMesh底层API
在最低级别,BMesh 提供了一个用于遍历圆盘虚幻、环循环和径向循环的 API,以及一组用于对网格进行局部更改的 Euler 运算符。
下面列出的函数代表网格工具用来操纵结构拓扑的“原始”或“原子”运算符。*这些函数的目的是提供一组可信赖的运算符来操纵网格拓扑,也可以是像构建块一样组合在一起以创建更复杂的工具。
在 BMesh 系统中,底层操作使用前缀 bmesh_kernel_,每个 Euler 都有一个逻辑逆。
- BM_vert_create/kill:创建/删除顶点
- BM_edge_create/kill:创建/删除边
- BM_face_create/kill:创建/删除面
- bmesh_kernel_split_edge_make_vert/join_edge_kill_vert
- bmesh_kernel_split_face_make_edge/join_face_kill_edge: 拆分/合并面
- bmesh_loop_reverse:反转 BMFace 的循环
底层API的目标是仅使用这些 Euler 运算符的组合,就可以实现任何非流形建模操作。 此外,每个运算符都利用存储在 BMesh 结构中的持久邻接信息来仅对局部拓扑进行修改。 这意味着每个运算符的运行时间仅受限于局部细节的复杂性,而不是整体网格密度。 最后,每个运算符都确保它作为输出生成的数据结构是完全有效的,因此工具作者不必直接操作和验证网格。
欧拉函数参考如下。
3.1分割边创建顶点
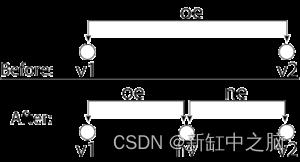
BMVert *bmesh_split_edge_make_vert(BMesh *bm, BMVert *tv, BMEdge *e, BMEdge **r_e)
取一条给定的边并将其一分为二,创建一个新的顶点。 原始边 OE 重新链接到 V1 和 NV 之间。 OE 然后从 V2 的圆盘循环移动到 NV 的。 新边 NE 链接到 NV 和 V2 之间,并添加到两个顶点圆盘循环。 最后遍历 OE 的径向循环,拆分它遇到的面循环。
返回值为指向新 BMVert 的指针。
3.2 连接边删除顶点
BMEdge *bmesh_kernel_join_edge_kill_vert(BMesh *bm, BMEdge *e_kill, BMVert *v_kill, const bool do_del, const bool check_edge_double, const bool kill_degenerate_faces)

获取指向边 (ke) 的指针和指向其顶点之一 (kv) 的指针,并折叠该顶点上的边。 首先将 ke 从 kv 和 tv 的圆盘循环中移除。 然后边缘oe被重新链接到ov和tv之间运行,并被添加到ov的圆盘循环中。 最后遍历 oe 的径向循环并更新其所有面循环。 请注意,为了让这个欧拉起作用,kv 必须恰好只有两条边重合在它上面(化合价为 2)。 可以使用 bmesh_kernel_split_face_make_edge、bmesh_kernel_join_face_kill_edge 和 bmesh_kernel_join_edge_kill_vert 的组合来构建更通用的边折叠函数。
返回值1表示成功,0表示失败。
3.3 拆分面创建边
BMFace *bmesh_kernel_split_face_make_edge(BMesh *bm, BMFace *f, BMLoop *l_v1, BMLoop *l_v2, BMLoop **r_l, BMEdge *e_example, const bool no_double)

将单个面中的两个顶点作为输入。 创建一条边,将原始面分成两个不同的区域。 其中一个区域被分配给原始面并被关闭。 第二个区域分配了一个新面。 请注意,如果输入顶点共享一条边,这将创建一个只有两条边的面。
返回指向新 BMFace 的指针。
3.4 合并面删除边
BMFace *bmesh_kernel_join_face_kill_edge(BMesh *bm, BMFace *f1, BMFace *f2, BMEdge *e)

获取由单个 2-manifold 边连接的两个面并将它们融合在一起。 面共享的边不得连接到在其径向循环中具有两个面的任何其他边。
上图对此进行了说明。 在此图中,情况 A 是唯一一种 join_face_kill_edge 将返回一个指示成功的值的情况。 如果工具作者想要像在情况 B 中那样连接具有多条边的两个单独的面,他们应该首先在多余的边上运行 JEKV。 在这种情况下,没有一条连接两个面的边可以安全地移除,因为它会导致面自身环回。
另请注意,参数的顺序决定了某些每个面孔的属性是否存在于结果面中。 例如顶点缠绕、材质索引、平滑标志等都是从 f1 而不是 f2 继承的。
返回 1 表示成功,0 表示失败。
3.5 示例:使用欧拉运算符拆分面

在上图中,我们展示了欧拉运算符如何简单地组合在一起以创建更复杂的效果。 我们从标记为 F1 的 4 边四边形开始。 通过先在边 E1 上运行 split_edge_make_vert,然后在 E2 上运行,我们将 F1 变成具有六边的多边形。 最后,我们运行 split_face_make_edge 来连接两个新顶点并将面从中间分开。
下面是实现源代码:
BMVert *v1, *v2;
BMFace *f2;
v1 = bmesh_kernel_split_edge_make_vert(e1);
v2 = bmesh_kernel_split_edge_make_vert(e2);
f2 = bmesh_kernel_split_face_make_edge(f1, v1, v2);
值得注意的是,工具编写者现在只需三行代码就可以完成使用旧的 EditMesh 系统需要几十行甚至一百行或更多行才能完成的工作。 此外,工具编写者不直接修改网格,维护一致数据结构的复杂性由 Eulers 内部代码干净利落地处理。
3.6 关于边和面的重要说明
工具作者应该意识到 Bmesh 数据结构在边和面方面可能会以意想不到的方式运行。 例如,一个只有两条边的面是完全有效的。 由此逻辑上可以得出,在任意两个顶点之间可以存在任意数量的边。
虽然可以利用这些独特的属性来创建高级建模功能,但工具作者应该非常小心地在工具完成执行时清理具有 2 条边的面和具有多条边的顶点对。 尽管不这样做不会对建模系统的稳定性造成任何危害,但让结构处于普通最终用户无法直观理解的状态并不是一件好事。
注意:我正在考虑从建模系统中完全移除 对只有2 个边的面的支持。
4、BMesh中级 API
BMesh 运算符(“bmops”)是 BMesh 不可或缺的一部分。 它们建立在低级 API 的基础上,通常在输入参数指定的网格区域上执行某些基本类型的网格编辑(尽管一些运算符只是返回输出而不影响网格),从而为编辑提供构建块 工具。
网格运算符的示例包括(有关完整列表,请参见 bmesh_opdefines.c):
- mirror:镜向
- bevel:斜角
- similarfaces:相似面
大多数编辑工具都会组合一个或多个运算符来完成一项工作。 与普通的Blender运算符不同,BMesh 运算符可以嵌套(即调用其他运算符),因此运算符通常还会组合一个或多个其他运算符来完成一项工作。
4.1 运算符限制
运算符用于编辑网格,但绝不能触及头标志(可见性、选择等)。 此权限仅提供给高级网格编辑工具。
4.2 私有标志层
BMesh API 为运算符私有的面、边和顶点提供了一组标志。 这些标志可以由客户端运算符代码根据需要使用(一个常见的例子是标记元素以供在另一个运算符中使用)。 每次调用运算符都会分配一个新的标志层并将其压入层堆栈,当运算符完成时,其标志层就会从堆栈中弹出。 这避免了顺序执行的运算符和嵌套运算符执行之间的标志冲突。
4.3 运算符插槽
运算符通过使用“运算符槽”接收输入并返回输出。 这些槽本质上是命名的、类型化的参数。 插槽还使参数成为可选参数:如果没有有意义的值,则不要填充插槽(尽管如果应包含必要输入的插槽为空,则运算符可能会失败)。
以下插槽类型可用:
- 整型
- 浮点型
- 指针 - 不要存储与此元素对应的数组
- 元素缓冲区 - 顶点/边/面的列表
- Map - 简单的哈希映射
插槽 API 允许轻松地从一个运算符的输出复制到另一个运算符的输入,允许在顺序或嵌套运算符的执行期间链接数据流。
5、BMesh顶层 API
工具将网格编辑器与Blender界面连接起来,用户可以直接运行或脚本调用。 示例包括挤出、环切、边缘选择等。
工具是 API 中唯一可以触及头标志的部分,允许工具影响网格的选择、接缝或其他用户可见的属性。
作为最佳实践,工具不应包含任何用于遍历网格的复杂逻辑,并且永远不应直接编辑网格。 对于网格遍历,它们应该依赖于遍历器和迭代器。 对于网格编辑,他们应该调用 BMesh 运算符。
6、未来的工作
- 无直接网格编辑:仅使用 Euler 运算符
作为最佳实践,网格结构的所有操作都应该使用这些函数来完成。 这将是有益的,因为欧拉函数将受益于更广泛的测试,变得非常稳定,从而增加依赖它们的 BMesh 工具的稳定性。
然而,目前许多 BMesh 算子直接编辑网格结构,而不是使用这些 Euler 算子。 合并后的目标应该是将所有 BMesh 运算符转换为使用 Euler 函数,并在必要时可能添加额外的 Euler 函数。
- 面上的洞
作为原始设计的一部分,BMesh 将能够处理单个面的多个边界,这将允许面中出现孔。 这已经成为第一次 BMesh 特征合并的非目标,因为我们选择稳定现有的 BMesh 特征集,为第一次 BMesh 合并做准备。
原文链接:BMesh数据结构解密 — BimANt
以上是关于Blender BMesh数据结构解密的主要内容,如果未能解决你的问题,请参考以下文章