视觉SLAMEDPLVO: Efficient Direct Point-Line Visual Odometry

Posted 2023-01-21 振华OPPO

Citations： L. Zhou, G. Huang, Y. Mao et al.EDPLVO: Efficient Direct Point-Line Visual Odometry[C].2022 International Conference on Robotics and Automation (ICRA).Philadelphia, PA, USA, 2022：7559-7565.

Keywords： Three-dimensional displays, Closed-form solutions, Automation, Optimization methods, Optimization, Visual odometry, Convergence

由美团发布的Direct Visual Odometry：EDPLVO，荣获2022最佳优秀论文。提出了一种将线段融合到光流法的新方法，显著减少了优化的变量数量，并满足共线约束。此外，引入了一种两步法来加速优化并证明其收敛性。与最先进的VO相比，EDPLVO不仅降低了优化的计算量，还提高了精度。

论文目录

• 摘要
• 一、引言
• 二、相关工作
• • A. 线条匹配
  • B. 基于特征的方法
  • C. 直接法
• 三、符号和公式
• 四、直接点线模型
• • A. 参数化共线 2D 点的 3D 点
  • B. 线的光度误差
  • C. 线关联的共线约束
  • D. 模型制定
  • E. 窗口优化
  • F. 两步最小化
• 五、前端
• • A.3D 线初始化
  • B. 二维线组合
• 六、实验结果
• • A. 数据集和指标
  • B. 与现有技术的比较
  • C. 消融实验
  • D. 运行时间
• 七、结论

摘要

一、引言

视觉同步定位和建图 （VSLAM） 是许多机器人和计算机视觉应用的基本模块，从自主导航到增强现实 （AR）。没有闭环的轻量级VSLAM系统通常被称为视觉里程计（VO）[3]，这对于需要在资源有限的嵌入式设备上进行实时姿态估计的应用非常重要。由于VSLAM和VO的重要性，它们在计算机视觉和机器人社区中获得了广泛的关注。

如今，深度学习技术在各种计算机视觉任务中优于传统方法。在VO方面，基于学习的方法近年来取得了重大进展[4]-[8]。但是，由于这些方法需要强大的GPU，因此对于嵌入式系统上的实时应用程序是不可行的。传统的VSLAM和VO系统仍然更适合这些应用。传统方法一般分为两类，即基于特征（间接）[9]和直接方法[1]。基于特征的方法长期以来一直主导着这一领域。同时，最近的研究[1]，[2]表明，即使在低纹理场景中，直接方法也表现出高精度和鲁棒性，而这些场景通常对基于特征的方法具有挑战性。因此，本文重点介绍了VO的直接法。

直接方法通常采用具有足够大渐变的像素，通常包括线上的角和点。在许多人造场景中，线上的点数量可能明显超过拐角，如图 2（a） 所示。通过光流跟踪角落是明确定义的[10]。但是，线上的跟踪点是有问题的，因为沿线存在一维歧义。丢弃共线约束可能会导致深度估计不太准确，如图2（b）所示。尽管已经探索了线来克服这个问题，但它们通常会显着增加优化中的计算量[2]，[11]。这项工作基于我们之前的工作DPLVO [2]，我们寻求加速计算。本文的主要贡献包括：

• 我们将光度误差扩展到线条。原始光度误差仅针对点定义，因此难以应用于线。我们没有像[2]中那样简单地将colllinear constraint引入代价函数中，而是提出了一种新方法来参数化3D共线点，以使将线合并到光度误差中成为可能。具体来说，我们证明了2D线上任何点的3D点都是由2D线的两个端点的反深度决定的。此属性可以显著减少变量的数量。同时，该方法在优化过程中完全满足共线约束，可以提高精度。

• 我们引入了一种两步法来限制由于在优化中引入长期线关联而导致的计算复杂性。在每次迭代中，我们首先使用固定的反深度和关键帧姿势拟合 3D 线。然后，我们使用新的线参数来调节反深度和关键帧位姿的优化。由此产生的两个优化问题很容易解决。我们证明了这种方法总是可以收敛的。

虽然本文侧重于VO，但这些想法也可以纳入直接视觉惯性里程计（VIO）系统[12]。

二、相关工作

点和线广泛存在于人造场景中。使用点和线的基于特征的直接 VSLAM 或 VO 已被广泛研究。

A. 线条匹配

使用线条的挑战之一是执行线路匹配。基于描述符的行匹配方法在以前的算法中被广泛采用[13]–[16]。行描述符 LBD [17] 通常用于此目的。由于传统的线路检测方法，如LSD [18]，可能不稳定，这可能会导致线路匹配失败[17]。尽管基于深度学习的线检测方法[19]-[23]显示出有希望的结果，但这些方法通常对计算要求很高。此外，由于移动摄像机观察到的 3D 线段在一部分出现在或移出摄像机的视野 （FoV） 时会发生变化，因此这种外观变化也可能导致匹配失败。最近，提出了基于跟踪的解决方案来克服这个问题。王等. [17] 提出利用空间和时间相干性进行线匹配的线流。在 [2] 中，提出了用于行匹配的跟踪-扩展-重新分发方法。这种方法从一条线上对一些点进行采样，然后通过最小化沿极线的光度误差来跟踪它们，这些光度误差可以自然地合并到DSO的前端[1]中。因此，我们采用这种方法来建立线关联。

B. 基于特征的方法

仅使用点 [9]、[24]–[26] 的基于特征的方法的性能在低纹理区域中会降低。线条可以补充低纹理环境中的点。针对点 [9]、[25]、[26] 的完善的 ORB-SLAM 框架可以很容易地扩展到线 [13]。但这种策略大大增加了前端和后端的计算负载[13]。室内环境中线条的结构可用于提高性能[27]，[28]。由于曼哈顿世界的假设，这些方法很难应用于户外场景。

C. 直接法

直接方法可最大程度地减少光度计误差，以估计相机姿势和点深度[1]，[29]。对于VO系统来说，漂移是不可避免的。最近的一些工作[30]，[31]将环路检测引入漂移校正的直接方法中。虽然闭环可以纠正漂移，但它只能事后纠正关键帧姿势的漂移。精确的动态跟踪姿势对于许多实时应用也很重要，例如运动规划、控制和 AR。 线条提供了另一种提高性能的选项。

光度计误差是测量参考图像和目标图像中点的强度值之间的差异。与可以为不同类型的要素定义几何距离的基于要素的方法不同，光度误差仅针对点定义。因此，直接方法很难扩展到生产线。在文献中，共线约束通常用于调节深度估计。在 [11] 和 [32] 中，将 3D 线拟合到共线点，然后将共线点投影到该线中。在这些方法中，线不会与点和关键帧姿势联合优化。在[2]中，将共线约束与光度计误差相结合，共同优化具有点和关键帧姿势的三维线。但不能保证在优化过程中可以完全满足共线约束，并且线显着增加了优化的计算负载。此外，[2] 中的 3D 线在其第一个具有两个自由度 （DoF） 的 2D 线观测的背投影平面中表示。尽管这种参数化减少了未知数的数量以加快优化速度，但二维线的估计误差可能会导致次优结果。此外，[2] 中的 3D 线是通过拟合到共线 3D 点来初始化的，这些点最初是在不考虑共线约束的情况下估计的。如果共线点的质量较差，如图2（b）所示，则3D线初始化将不准确甚至失败，因此3D线可能会降级或失去调节共线点深度估计的能力。在本文中，我们试图克服这些缺点，并展示如何有效地优化具有点和关键帧姿势的3D线的完整四自由度。

三、符号和公式

作者定义了本文用到的符号，使用粗体字母来表示向量和矩阵，并分别使用斜体小写和斜体大写来表示标量和函数。主要定义了光度误差的表达式和3D线段的普吕克坐标。感兴趣的可以看原文。

四、直接点线模型

A. 参数化共线 2D 点的 3D 点

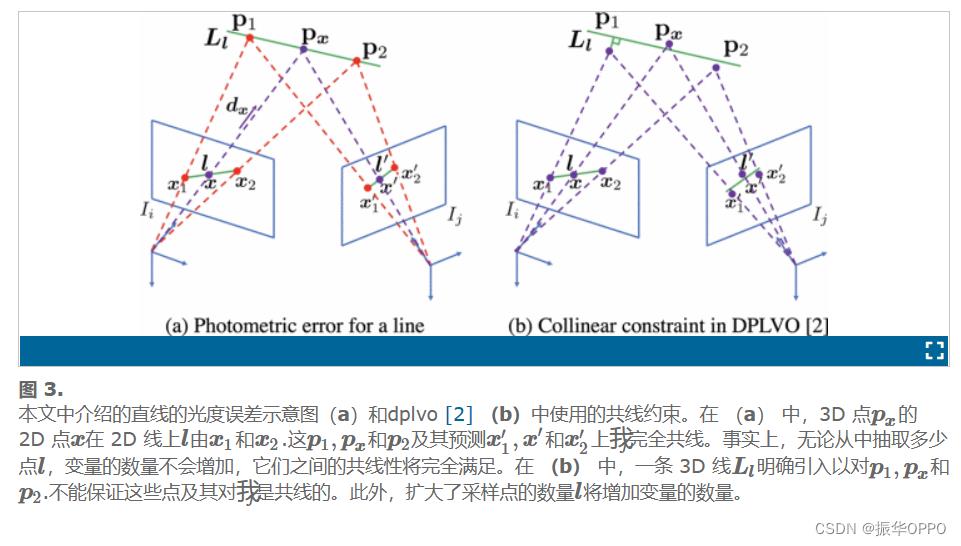
B. 线的光度误差

C. 线关联的共线约束

在上一节中，我们将线条合并到光度误差中。作为无界对象，3D线可以长时间存在于相机的FoV中。我们采用 [2] 中介绍的方法建立线关联，并引入共线约束来调节端点的深度，如图 4 所示。

D. 模型制定

E. 窗口优化

我们采用滑动窗口策略来优化全部成本（12），以平衡精度和效率，如图4所示。边缘化通常在以前的直接VO算法中采用[1]，[2]。由于3D线可以长时间存在于相机的FoV中，因此我们希望在可见时不断更新线。此外，由于 （12） 中可能包含错误的线关联，因此当我们在优化过程中发现点到线的距离 （4） 太大时，我们希望删除错误的线关联。错误的联想一旦被边缘化，就很难被消除。因此，这项工作不采用边缘化方法。相反，我们采用类似于 [9] 中描述的局部捆绑盘调整的优化策略。具体来说，我们优化滑动窗口内的主动姿势以及可见的点和线。（12） 中的其他参数是固定的。让我们以术语为例EL在（11）中定义为例。如果qi，1和qi，2变得不可见，它们被固定，如图4（a）中的灰点所示。因此EL成为一个只依赖于L.对于长 3D 线段，此策略可能会引入许多先前的共线约束 [2]。我们采用 [2] 中介绍的方法来加快计算速度。在此框架中可以轻松消除错误的关联和较大的光度误差。我们采用 [37] 中引入的思想来有效地解决由此产生的优化问题，其中 Schur 补集是增量构造的，如果所涉及的参数的变化很大，则残差被重新线性化。

F. 两步最小化

线条放大了未知数的数量，并与点和姿势相关联。因此，联合优化带有点和姿势的线会增加计算负载。我们引入了一个两步法来最小化（12）。让我们首先关注（12）的最后一个术语。点、线和姿势在这个术语中是相关的。给定相机姿势和 2D 端点的反深度，此问题等效于将 3D 线拟合到点集。另一方面，如果行参数在L^是固定的，得到的成本函数E对于姿势和反深度可以像仅考虑光度误差一样有效地最小化。我们可以迭代这两个步骤。该算法称为两步最小化，总结在算法 1 中。请注意，一个Levenberg-Marquardt（LM）步骤可能包括多个迭代以降低成本[38]。一个问题是两步最小化算法是否会收敛。以下定理给出了这个问题的答案。

五、前端

我们的前端类似于DPLVO [2]，它管理点，线和帧。主要区别在于 3D 线初始化和 2D 线组合。

A.3D 线初始化

在 DPLVO [2] 中，某些点是从新的 2D 线中采样的。然后单独估计它们的 3D 点，而不考虑共线约束。通过拟合这些 3D 点来初始化 3D 线。如果如图2（b）所示的3D点精度较低，则线路初始化将降级甚至失败，从而影响算法的稳定性。在本文中，我们考虑在线路初始化步骤中施加共线性。具体来说，给定一条新的 2D 线l，我们通过最小化光度误差来跟踪后续图像中沿极线采样的 2D 点，就像在 DPLVO 中所做的那样。这形成了一组对应关系x↔x′.由于姿势误差和沿线的模糊性，这种跟踪不太可能生成准确的点-点对应关系l.但它可以生成准确的线-线对应关系。我们拟合一条 2D 线l′到跟踪点x′.假设π和π′是 的反向投影平面l和l′分别。我们计算 3D 逐行三角测量 [17] 如果角度π和π′大于 3°。然后端点的反深度l可以计算，然后在后续的线路跟踪中使用。受 [17] 的激励，当新的线关联可用时，我们通过平均来更新 3D 端点。追踪期间具有较大光度误差的线将被移除，然后从这些线采样的点将被视为 DSO [1] 中的法线。

B. 二维线组合

LSD线检测器[18]可以返回2D线的几个段，如图5（a）所示。在 DPLVO [2] 中，具有相似参数的附近线被合并。这种方法可以集成相邻但不同的线，如图5（a）中的红色虚线矩形所示。在这种情况下，合并的线可能位于低梯度区域中。因此，当合并线的投影重叠或两条线的平均梯度之间的角度很大时，我们不会合并两条线。如图5所示，合并的线可以穿过低梯度区域。因此，原始线段被投影到合并线。2D 点分别从投影线段中采样。如果近似平行线彼此太近，我们总结沿线梯度的大小，并保留具有最大累积幅度的那个。我们还尝试将新检测到的行与现有行合并，以避免引入新参数。

六、实验结果

A. 数据集和指标

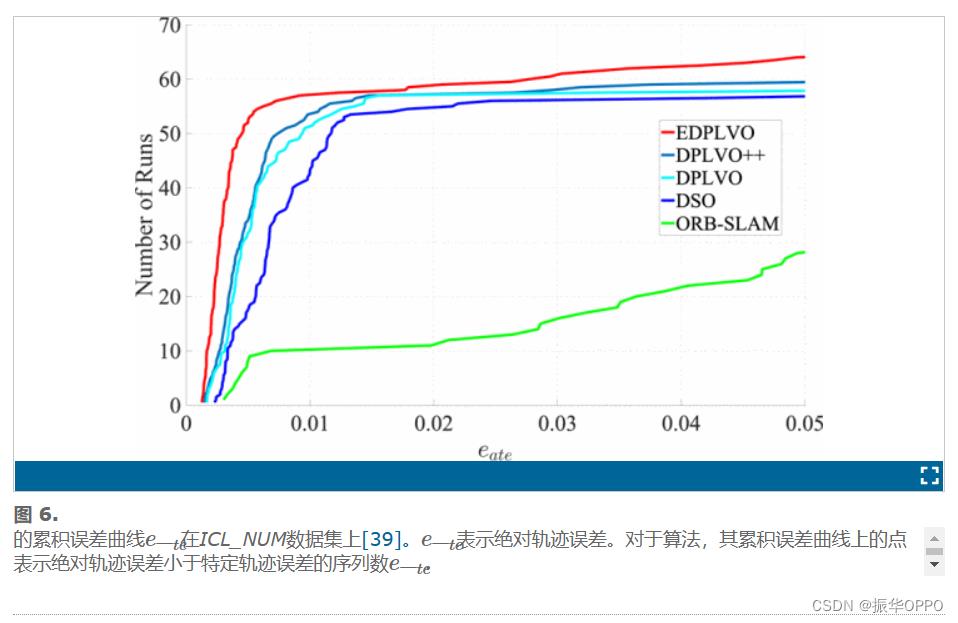
我们使用ICL-NUIM [39]和TUM monoVO [40]数据集来评估比较算法的性能。ICL-NUIM数据集包含8个室内序列，TUM monoVO数据集包含来自室内和室外环境的50个闭环序列。为了处理非确定性行为，我们前后运行每个序列 10 次，并采用累积误差曲线来总结结果，如 [1] 所示。该曲线显示了误差低于某个阈值的跟踪序列的数量，这揭示了算法的准确性和鲁棒性。ICL-NUIM数据集为每个序列提供真实轨迹。因此，我们比较了绝对轨迹误差e一te的比较算法。另一方面，TUM monoVO数据集不提供地面真相轨迹。相反，它提供了闭环基本事实。我们采用对齐误差e一我gn、旋转漂移er和刻度漂移es在 [40] 中定义以评估算法的性能。

B. 与现有技术的比较

我们将我们的算法（称为EDPLVO）与最先进的视觉里程计算法进行比较，包括DSO [1]，DPLVO [2]和ORB-SLAM [9]。图6和图7分别显示了ICL-NUIM数据集[39]和TUM单VO数据集[40]的结果。结果表明，我们的算法优于其他算法。ORB-SLAM和DSO的结果来自DSO的网站[1]。我们的算法与DPLVO密切相关。为了公平比较，我们使用第五节中介绍的线路管理方法来替换DPLVO中的对应方法，使两种算法具有相同的前端，并将此方法命名为DPLVO++。如图 6 所示，DPLVO++ 产生的结果比 DPLVO 更好。由于这两个数据集在低纹理环境中很丰富，因此 ORB-SLAM 的性能不佳。由于提出的线光度误差（10）将精确的共线性强加于光度误差，并且优化了3D线的整个四个自由度，因此我们的算法实现了比DPLVO++更好的精度。

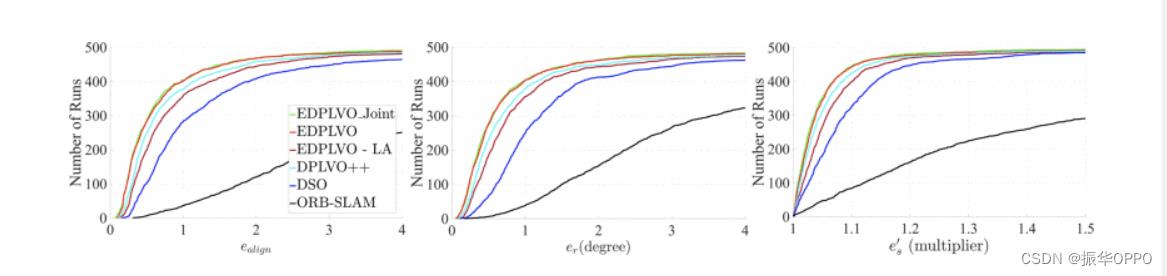
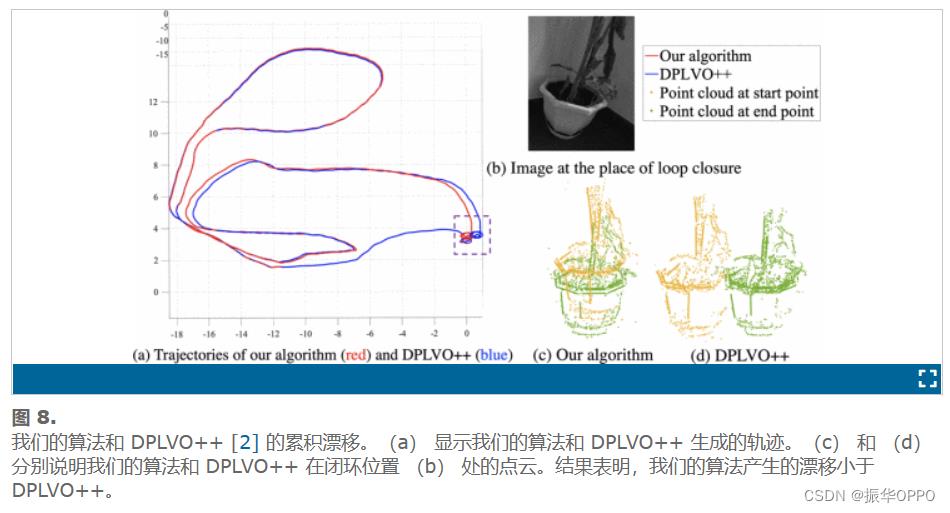
图 1 展示了我们的算法生成的点云和线。图 8 分别显示了我们的算法和 DPLVO++ [2] 生成的闭环位置的轨迹和点云。结果表明，EDPLVO的漂移小于DPLVO++。

C. 消融实验

然后，我们研究算法不同组件的影响。我们考虑算法的两种变体：

• EDPLVO - LA：未建立线路关联。也就是说，（12）中的共线性项被删除了。

• EDPLVO_Joint：共同调整成本函数 （12） 中的所有变量。我们采用 [34] 中引入的四个 DoF 表示来参数化 3D 线。

图 7 说明了结果。由于调节共线点，EDPLVO - LA优于DSO。此外，EDPLVO - LA的性能接近DPLVO++ [2]。EDPLVO 优于 EDPLVO - LA 并不奇怪，因为线关联引入了额外的姿势约束。EDPLVO和EDPLVO_Joint的结果之间的差异很小，但EDPLVO的效率要高得多，如下所述。

D. 运行时间

本文的主要贡献集中在后端。因此，我们评估算法后端的运行时，EDPLVO_Joint，DSO [1] 和 DPLVO++ [2]。运行时间是在具有i7 3.4 GHZ CPU和16G内存的笔记本电脑上使用TUM单VO数据集获得的。我们的算法后端 EDPLVO_Joint、DSO [1] 和 DPLVO++ [2] 的平均运行时间分别约为 96ms、123 ms、141 ms 和 172 ms。我们的算法在比较的算法中具有最快的后端。请注意，尽管EDPLVO_Joint中的 3D 线在四个 DoF [34] 中参数化，并且 DPLVO++ 对 3D 线采用双自由度参数化，但EDPLVO_Joint仍然比 DPLVO++ 快。

七、结论

本文提出一种新型的直接VO算法。我们证明了二维线上像素的三维点是由二维线端点的反深度决定的，这使得将线合并到光度误差中是可行的。与DPLVO [2]相比，我们的算法显著减少了优化中的变量数量，并使共线性完全满足。此外，我们引入了一种两步优化方法来加速优化并证明其收敛性。实验结果表明，与最先进的VO算法相比，该算法显著降低了优化的计算负荷，获得了更准确的结果。

Nowadays, deep learning technology outperforms traditional methods in various computer visual tasks. recent research shows that the direct method demonstrates high accuracy and robustness. Drift is inevitable for a VO system.