11. 分类损失最小化

Posted 2023-02-23 starrow

2.2.2 分类损失最小化

针对分类输出值的离散性，通常用矩阵定义损失。比如，对于普通患者被机器人医生诊断为严重，可以设定一个损失值；对于重症患者被诊断为健康，可以设定另一个损失值。设输出有K个类别，总共有K × K种不同情况需要设定损失值，用一个K × K的矩阵L表示，第k行第l列的元素为，将实际属于类别k的实例归入类别l的损失值。

理论上对于不同的误分类情况，可以设定各异的损失值。例如，将健康人诊断为健康的损失值定为0，将普通患者诊断为严重的损失值定为1，将严重患者诊断为健康的损失值定为3。不过，最常用的损失函数采用的是最简单的方案：将分类正确的损失值定为0，将分类错误的损失值定为1而无论具体的错误如何。这样的矩阵称为0–1损失矩阵。比如有3个输出类别的0–1损失矩阵为：

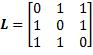
损失矩阵也可以表示为函数形式L(g, h(x))。0–1损失函数可以用恒等函数（Identity function）定义：

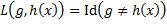
此处恒等函数的自变量用1表示真值、0表示假值，所以当g ≠ h(x)时取值1，当g = h(x)时取值0。有了损失函数，下一步就是写出损失期望值。与回归的做法一样，将该期望值表示为关于X的条件期望：

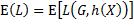
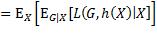
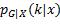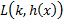在应用内层期望算子时，将X当成常数，求出结果后再把X当作随机变量求外层期望值。因为G的取值是离散的，内层期望可以写为，G取各值时损失与相应概率乘积之和。不妨设G的取值集合为G = 1, 2,..., K，当输入为x，预测类别为h(x)时，实际类别为k的概率是 ，损失是 ，于是有：

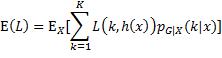
要使损失期望值最小化，就要使内层条件期望取最小值。代入0–1损失函数，有：

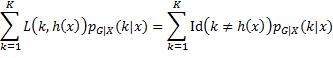
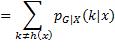
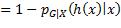
可见，只要选择h(x)值等于概率最大的类别，就能获得条件期望的最小值。例如，G = 1, 2, 3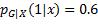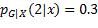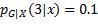， ， ， ，损失的条件期望为：

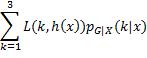
损失矩阵为：

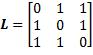
假如取h(x) = 1，当实际类别为1时，损失是L(1, 1) = 0；当实际类别为2时，损失是L(2, 1) = 1；当实际类别为3时，损失是L(3, 1) = 1；它们的和等于0.6 × 0 + 0.3 × 1 + 0.1 × 1 = 0.4。假如取h(x) = 2，各个类别的概率所乘的系数就会是损失矩阵的第二列，结果是0.6 × 1 + 0.3 × 0 + 0.1 × 1 = 0.7。同理，取h(x) = 3会导致损失的条件期望等于0.9。所以，当h(x)等于概率最大的类别1时，损失的条件期望最小。

综上所述，对于任何输入值，分类的预测函数值应该使损失关于该输入值的条件期望最小：

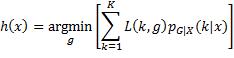
在采取0–1损失函数时，预测函数的取值要求简化为，最大化输出关于输入的条件概率：

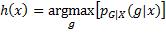
这是一个有趣的结论，因为我们直觉上也会选择概率最大的类别作为预测的输出值，而上述分析表明这仅在采用0–1损失函数时才有道理。假如为各种误分类情况设定不同的损失值，合理的预测输出就会不再是概率最大的类别。例如，设想一个极端的情况，将患者诊断为健康的损失值为1，将健康的人误诊为患病的损失值为0，那么只要求诊者患病的概率不为0——即使患病的概率等于0.01，而健康的概率为0.99——也会被诊断为患病。