Mathematical Problems Caused by CCD

Posted 2023-01-20 m0_74246769

     In recent years, due to highly complex interactions between various internal and external influences, including pests, pathogens, bee population diversity and environmental changes. CCD occurred in 2007 as a result of reduced bee viability and nutrition, exposure to agricultural chemicals, and quality of colony management resulting in reduced colony survival in beekeeping operations. Based on this, the following mathematical problems are proposed:

1. Develop a model to determine the number of bee colonies over time

2. Sensitivity analysis of the model was conducted to determine which factors had the greatest influence on bee colony size

3. Model and predict how many bee hives will be needed to pollinate 81,000 square meters of land

The author's brief analysis is as follows:

     First of all, in the first question, if the bees studied belong to experimental bees, that is, bees living in a closed laboratory, other conditions are completely consistent with the natural environment except the natural enemy factors (that is, the living environment is almost completely consistent with the natural environment), so the factors of immigration rate and outflow rate can be ignored, and the model is established under the premise that the experiment time is 1 year. At this point, a simple ordinary differential equation model can be established to solve the problem. In this case, the population of bees is only affected by birth rate and death rate, so it is only necessary to establish a differential equation model according to the birth rate and death rate of bees in different time periods obtained in the experiment, and according to the biological environmental tolerance is almost constant, so the environmental tolerance K in the laboratory is roughly equal to that in the natural environment. Theoretically, the Malthus model can be established. But in fact, this is based on the ideal situation, in which bee birth and death rates are very stable and the population does not reach the environmental capacity K for a certain period of time, but according to biology, this rarely happens in nature. Therefore, birth and death rates need to be considered more carefully. For further consideration, if the bee population reaches the environmental tolerance K within a certain period of time, it is still lack of rigor and authenticity to consider only the birth rate and death rate, and further consider the inherent growth rate r, and establish an ordinary differential equation based on the Logistic model for solving:

 

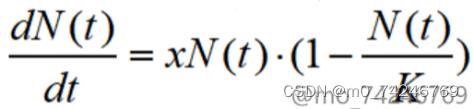
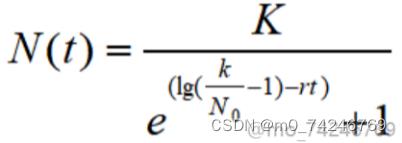
Through software mapping, we get the final result

       In the second question, we first added some data, through the data we know: the more bees, the more stable the temperature in the hive; When the number of bees reaches a certain level, the temperature of the hive can be kept between 34 degrees Celsius and 35 degrees Celsius. Too high or too low temperature is not conducive to bee development and reproduction. Next, we carried out sensitivity analysis on natural growth rate, natural growth rate, environmental tolerance K and proportion of each age group respectively by combining Logistic retarded growth model with direct derivative function, and successfully reached the following conclusions: Age group, inherent growth rate, environmental tolerance (environment). The natural growth rate and age group had the greatest influence on bee population size, followed by environmental tolerance, that is, environmental factors. 

     For the third question, we assume that all the flowers in this area are distributed within the effective pollination range of bees, and an average of 20,000 bees in each hive can go out to collect honey, each bee can only transmit 2000 flowers at most, and bees generally collect honey within 6 kilometers from the hive. Therefore, we can get the final result by performing some simple mathematical operations. Furthermore, a model is established to verify its accuracy.