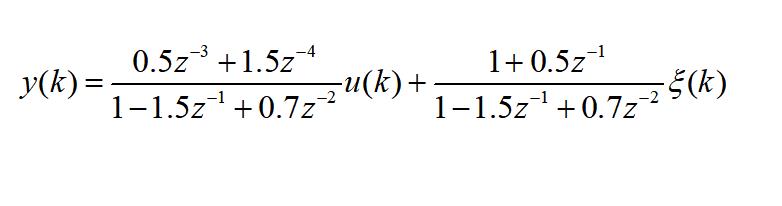《系统辨识》作业CSU
Posted yangbocsu
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了《系统辨识》作业CSU相关的知识，希望对你有一定的参考价值。
#By 赶路人_87HZ
作业一 递推最小二乘法参数辨识
设被辨识系统的数学模型由下式描述：
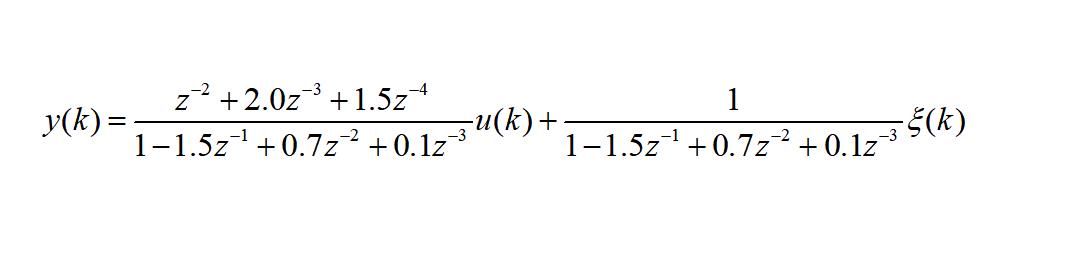
式中x(k)为方差为0.1的白噪声。要求：
-
当输入信号u(k)是方差为1的白噪声序列时，利用系统的输入输出数据在线辨识上述模型的参数；
-
当输入信号u(k)是幅值为1的逆M序列时，利用系统的输入输出数据在线辨识上述模型的参数；
-
当输入信号u(k)是单位阶跃信号时，利用系统的输入输出数据在线辨识上述模型的参数；
分析比较在不同输入信号作用下，对系统模型参数辨识精度的影响。
解：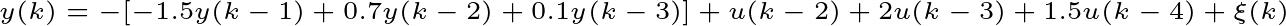
【参考代码】
①方差为1的白噪声序列
%#By 赶路人_87HZ 递推最小二乘参数估计（RLS） 输入信号u(t)= 方差为1的白噪声序列
clear all; close all;
a=[1 -1.5 0.7 0.1]';
b=[1 2 1.5]'; d=2; %对象参数
na=length(a)-1; nb=length(b)-1; %na=3、nb=2为A、B阶次
L=400; %仿真长度
uk=zeros(d+nb,1); %输入初值：uk(i)表示u(k-i)
yk=zeros(na,1); %输出初值
u=randn(L,1); %输入采用白噪声序列
xi=sqrt(1)*randn(L,1); %白噪声序列 方差=1
theta=[a(2:na+1);b]; %对象参数真值
thetae_1=zeros(na+nb+1,1); %thetae初值
P=10^6*eye(na+nb+1);
for k=1:L
phi=[-yk;uk(d:d+nb)]; %此处phi为列向量
y(k)=phi'*theta+xi(k); %采集输出数据
%递推最小二乘法
K=P*phi/(1+phi'*P*phi);
thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);
P=(eye(na+nb+1)-K*phi')*P;
%更新数据
thetae_1=thetae(:,k);
for i=d+nb:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=na:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
end
plot([1:L],thetae); %line([1,L],[theta,theta]);
xlabel('k'); ylabel('参数估计a、b');
legend('a_1','a_2','a_3','b_0','b_1','b_2'); axis([0 L -2 3]);
title("输入信号为方差为1的白噪声序列 的参数辨识")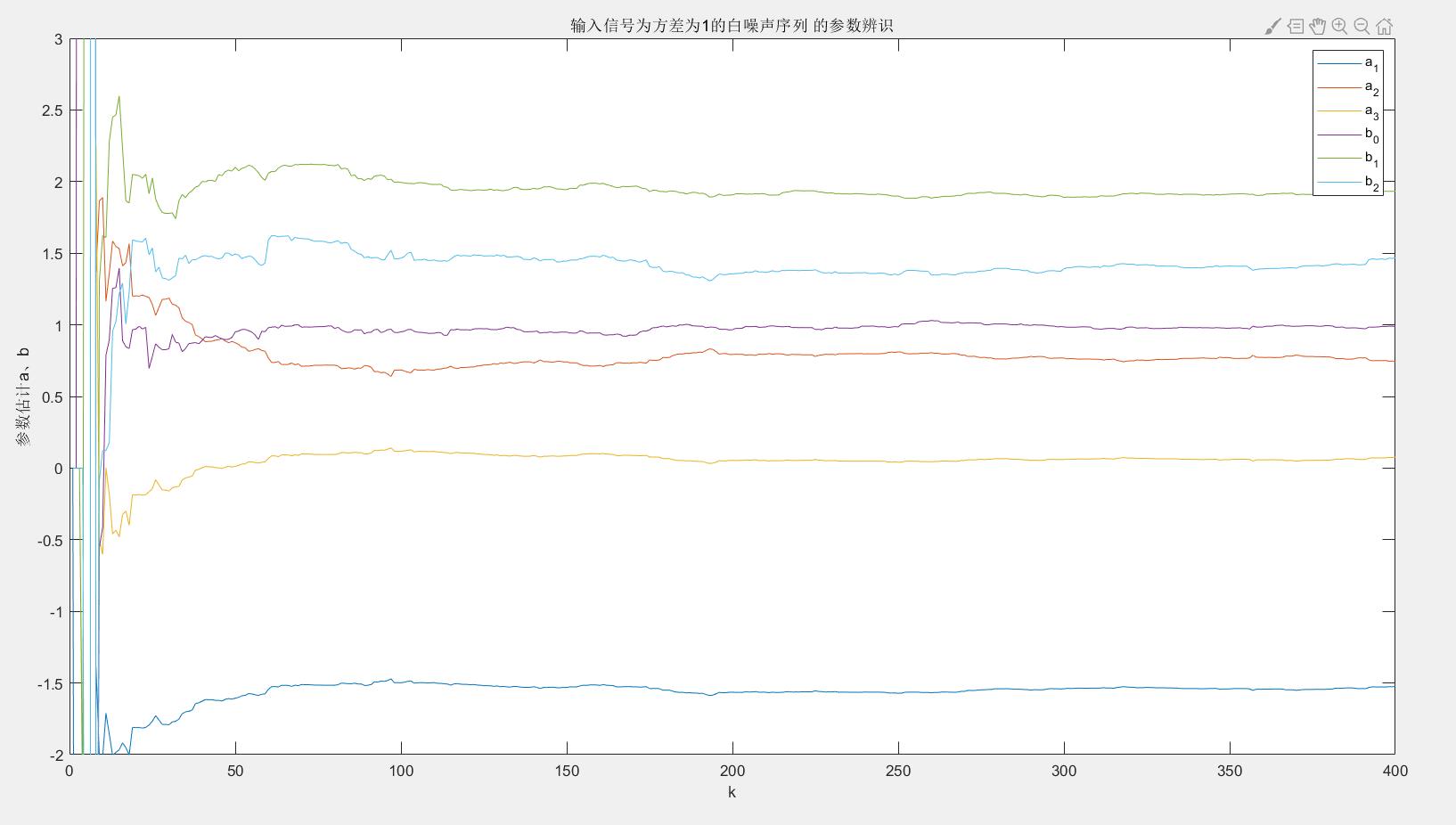
②幅值为1的逆M序列
%#By 赶路人_87HZ 递推最小二乘参数估计（RLS） 输入信号u(t)= 幅值为1的逆M序列
clear all; close all;
a=[1 -1.5 0.7 0.1]';
b=[1 2 1.5]'; d=2; %对象参数
na=length(a)-1; nb=length(b)-1; %na=3、nb=2为A、B阶次
L=400; %仿真长度
uk=zeros(d+nb,1); %输入初值：uk(i)表示u(k-i)
yk=zeros(na,1); %输出初值
%u=randn(L,1); %输入采用白噪声序列
xi=sqrt(1)*randn(L,1); %白噪声序列 方差=1
theta=[a(2:na+1);b]; %对象参数真值
thetae_1=zeros(na+nb+1,1); %thetae初值
P=10^6*eye(na+nb+1);
%M序列及逆M序列的产生
%M序列长度 L=400; %仿真长度
x1=1; x2=1; x3=1; x4=0; %移位寄存器初值xi-1、xi-2、xi-3、xi-4
S=1; %方波初值
for k=1:L
M(k)=xor(x3,x4); %进行异或运算,产生M序列
IM=xor(M(k),S); %进行异或运算,产生逆M序列
if IM==0
u(k)=-1;
else
u(k)=1;
end
S=not(S); %产生方波
x4=x3; x3=x2; x2=x1; x1=M(k); %寄存器移位
phi=[-yk;uk(d:d+nb)]; %此处phi为列向量
y(k)=phi'*theta+xi(k); %采集输出数据
%递推最小二乘法
K=P*phi/(1+phi'*P*phi);
thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);
P=(eye(na+nb+1)-K*phi')*P;
%更新数据
thetae_1=thetae(:,k);
for i=d+nb:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=na:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
end
plot([1:L],thetae); %line([1,L],[theta,theta]);
xlabel('k'); ylabel('参数估计a、b');
legend('a_1','a_2','a_3','b_0','b_1','b_2'); axis([0 L -2 4]);
title("输入信号为幅值为1的逆M序列 的参数辨识")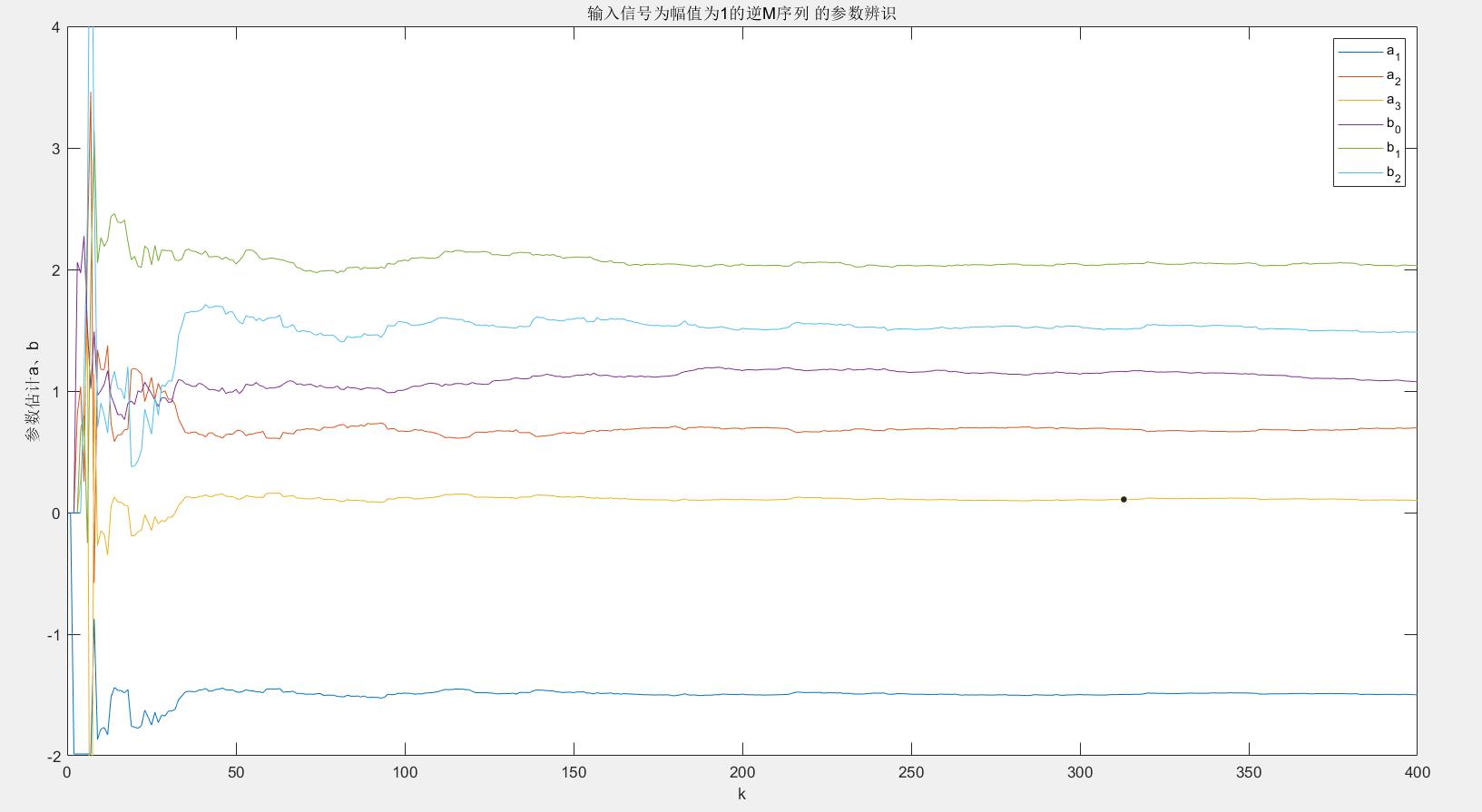
③单位阶跃信号
%#By 赶路人_87HZ 递推最小二乘参数估计（RLS） 输入信号u(t)=单位阶跃信号
clear all; close all;
a=[1 -1.5 0.7 0.1]';
b=[1 2 1.5]'; d=2; %对象参数
na=length(a)-1; nb=length(b)-1; %na=3、nb=2为A、B阶次
L=400; %仿真长度
uk=zeros(d+nb,1); %输入初值：uk(i)表示u(k-i)
yk=zeros(na,1); %输出初值
u=ones(L,1);%输入采用单位阶跃信号
xi=sqrt(1)*randn(L,1); %白噪声序列 方差=1
theta=[a(2:na+1);b]; %对象参数真值
thetae_1=zeros(na+nb+1,1); %thetae初值
P=10^6*eye(na+nb+1);
for k=1:L
phi=[-yk;uk(d:d+nb)]; %此处phi为列向量
y(k)=phi'*theta+xi(k); %采集输出数据
%递推最小二乘法
K=P*phi/(1+phi'*P*phi);
thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);
P=(eye(na+nb+1)-K*phi')*P;
%更新数据
thetae_1=thetae(:,k);
for i=d+nb:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=na:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
end
plot([1:L],thetae); %line([1,L],[theta,theta]);
xlabel('k'); ylabel('参数估计a、b');
legend('a_1','a_2','a_3','b_0','b_1','b_2'); axis([0 L -2 1.5]);
title("输入信号为 输入信号u(t)=单位阶跃信号 的参数辨识")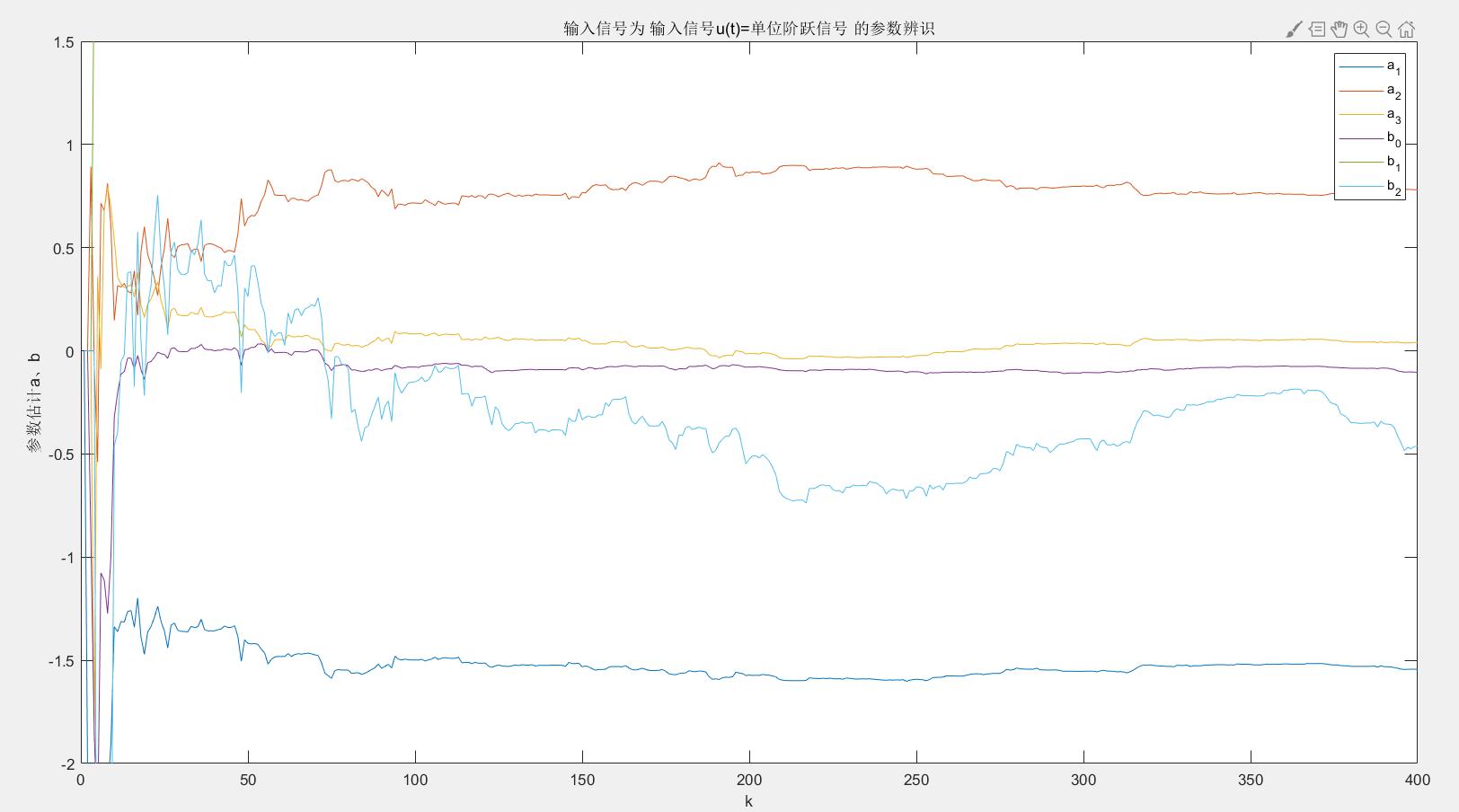
作业二 最小方差自校正控制实验
设二阶纯滞后被控对象的数学模型参数未知或慢时变，仿真实验时用下列模型：
式中x(k)为方差为0.1的白噪声。要求：
(1) 当设定输入yr(k)为幅值是10的阶跃信号时，设计最小方差直接自校正控制算法对上述对象进行闭环控制；
(2) 当设定输入yr(k)为幅值是10的方波信号时，设计最小方差直接自校正控制算法对上述对象进行闭环控制；
(3) 如果被控对象模型改为：
重复上述（1）、（2）实验，控制结果如何？分析原因。
【参考代码】
被控对象模型未修改前的
(1) %幅值是10的阶跃信号
%#By 赶路人_87HZ 最小方差直接自校正控制 输入信号u(t)=%幅值是10的阶跃信号
clear all;close all;
a=[1 -1.5 0.7]; b=[2.5 1.5]; c=[1 0.5]; d=3; %对象参数
na=length(a)-1; nb=length(b)-1; nc=length(c)-1; %计算阶次
nh=nb+d-1; ng=na-1; %nh 为多项式 H 的阶次,ng 为多项式 G 的阶次
L=400;
uk=zeros(d+nh,1);
yk=zeros(d+ng,1);
yek=zeros(nc,1); %最优输出预测估计初值
yrk=zeros(nc,1);
xik=zeros(nc,1);
yr=10*[ones(L+d,1)]; %幅值是10的阶跃信号
xi=sqrt(0.1)*randn(L,1);%方差为 0.1 的白噪声序列
thetaek=zeros(na+nb+d+nc,d);
P=10^6*eye(na+nb+d+nc);
for k=1:L
time(k)=k;
y(k)=-a(2:na+1)*yk(1:na)+b*uk(d:d+nb)+c*[xi(k);xik];%采集输出数据
phie=[yk(d:d+ng);uk(d:d+nh);-yek(1:nc)];
K=P*phie/(1+phie'*P*phie);
thetae(:,k)=thetaek(:,1)+K*(y(k)-phie'*thetaek(:,1));
P=(eye(na+nb+d+nc)-K*phie')*P;
ye=phie'*thetaek(:,d);%预测输出估计值
%提取辨识参数
ge=thetae(1:ng+1,k)';
he=thetae(ng+2:ng+nh+2,k)';
ce=[1 thetae(ng+nh+3:ng+nh+nc+2,k)'];
if abs(ce(2))>0.9
ce(2)=sign(ce(2))*0.9;
end
if he(1)<0.1
he(1)=0.1;%设 h0 的下界为 0.1
end
uu=[yr(k+d:-1:k+d-min(d,nc))];
u(k)=(-he(2:nh+1)*uk(1:nh)+ce*[yr(k+d:-1:k+d-min(d,nc));yrk(1:nc-d)]-ge*[y(k);yk(1:na-1)])/he(1);%求控制量
%更新数据
for i=d:-1:2
thetaek(:,i)=thetaek(:,i-1);
end
thetaek(:,1)=thetae(:,k);
for i=d+nh:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=d+ng:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
for i=nc:-1:2
yek(i)=yek(i-1);
yrk(i)=yrk(i-1);
xik(i)=xik(i-1);
end
if nc>0
yek(1)=ye;
yrk(1)=yr(k);
xik(1)=xi(k);
end
end
%figure(1);
subplot(2,2,1);
plot(time,yr(1:L),'r:',time,y);
xlabel('k');ylabel('y_r(k)、y(k)');
legend('y_r(k)','y(k)');axis([0 L -100 100]);
title('输入为阶跃信号');%幅值是10的阶跃信号
subplot(2,2,2);
plot(time,u);
xlabel('k');ylabel('u(k)');axis([0 L -100 100]);
%figure(2);
subplot(2,2,3);
plot([1:L],thetae(1:ng+1,:),[1:L],thetae(ng+nh+3:ng+2+nh+nc,:));
xlabel('k');ylabel('参数估计 g,c');
legend('g_0','g_1','c_1');axis([0 L -3 4]);
title('输入为阶跃信号');
subplot(2,2,4);
plot([1:L],thetae(ng+2:ng+2+nh,:));
xlabel('k');ylabel('参数估计 h');
legend('h_0','h_1','h_2','h_3');axis([0 L 0 8]);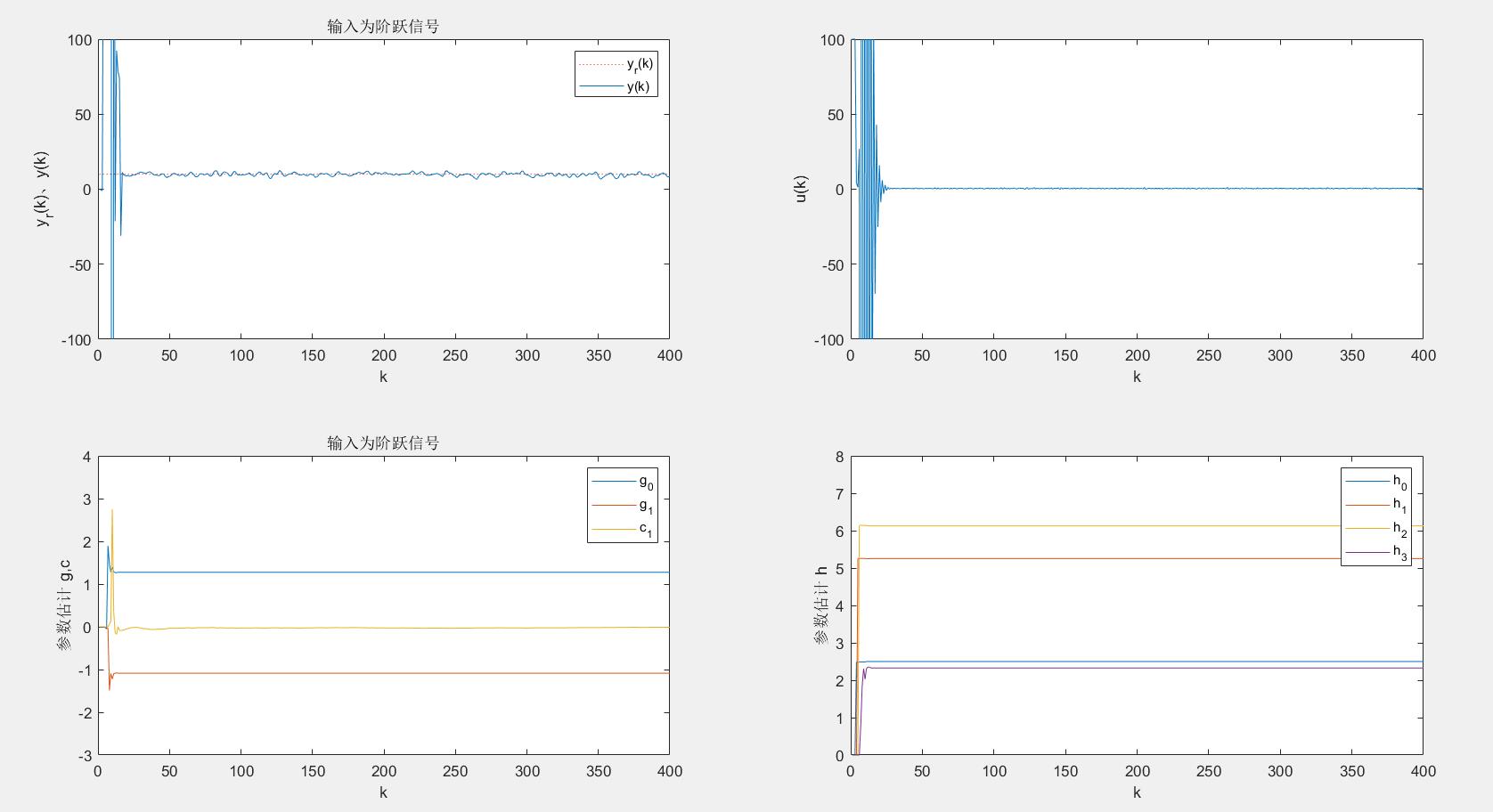 
(2)%幅值是10的方波信号
%#By 赶路人_87HZ 最小方差直接自校正控制 输入信号u(t)=%幅值是10的阶跃信号
clear all;close all;
a=[1 -1.5 0.7]; b=[2.5 1.5]; c=[1 0.5]; d=3; %对象参数
na=length(a)-1; nb=length(b)-1; nc=length(c)-1; %计算阶次
nh=nb+d-1; ng=na-1; %nh 为多项式 H 的阶次,ng 为多项式 G 的阶次
L=400;
uk=zeros(d+nh,1);
yk=zeros(d+ng,1);
yek=zeros(nc,1); %最优输出预测估计初值
yrk=zeros(nc,1);
xik=zeros(nc,1);
yr=10*[ones(L/4,1);-ones(L/4,1);ones(L/4,1);-ones(L/4+d,1)];% 期望输出 ②%幅值是10的方波信号
xi=sqrt(0.1)*randn(L,1);%方差为 0.1 的白噪声序列
thetaek=zeros(na+nb+d+nc,d);
P=10^6*eye(na+nb+d+nc);
for k=1:L
time(k)=k;
y(k)=-a(2:na+1)*yk(1:na)+b*uk(d:d+nb)+c*[xi(k);xik];%采集输出数据
phie=[yk(d:d+ng);uk(d:d+nh);-yek(1:nc)];
K=P*phie/(1+phie'*P*phie);
thetae(:,k)=thetaek(:,1)+K*(y(k)-phie'*thetaek(:,1));
P=(eye(na+nb+d+nc)-K*phie')*P;
ye=phie'*thetaek(:,d);%预测输出估计值
%提取辨识参数
ge=thetae(1:ng+1,k)';
he=thetae(ng+2:ng+nh+2,k)';
ce=[1 thetae(ng+nh+3:ng+nh+nc+2,k)'];
if abs(ce(2))>0.9
ce(2)=sign(ce(2))*0.9;
end
if he(1)<0.1
he(1)=0.1;%设 h0 的下界为 0.1
end
uu=[yr(k+d:-1:k+d-min(d,nc))];
u(k)=(-he(2:nh+1)*uk(1:nh)+ce*[yr(k+d:-1:k+d-min(d,nc));yrk(1:nc-d)]-ge*[y(k);yk(1:na-1)])/he(1);%求控制量
%更新数据
for i=d:-1:2
thetaek(:,i)=thetaek(:,i-1);
end
thetaek(:,1)=thetae(:,k);
for i=d+nh:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=d+ng:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
for i=nc:-1:2
yek(i)=yek(i-1);
yrk(i)=yrk(i-1);
xik(i)=xik(i-1);
end
if nc>0
yek(1)=ye;
yrk(1)=yr(k);
xik(1)=xi(k);
end
end
%figure(1);
subplot(2,2,1);
plot(time,yr(1:L),'r:',time,y);
xlabel('k');ylabel('y_r(k)、y(k)');
legend('y_r(k)','y(k)');axis([0 L -50 50]);
title('输入为方波信号');%幅值是10的方波信号
subplot(2,2,2);
plot(time,u);
xlabel('k');ylabel('u(k)');axis([0 L -100 100]);
%figure(2);
subplot(2,2,3);
plot([1:L],thetae(1:ng+1,:),[1:L],thetae(ng+nh+3:ng+2+nh+nc,:));
xlabel('k');ylabel('参数估计 g,c');
legend('g_0','g_1','c_1');axis([0 L -3 4]);
title('输入为方波信号');
subplot(2,2,4);
plot([1:L],thetae(ng+2:ng+2+nh,:));
xlabel('k');ylabel('参数估计 h');
legend('h_0','h_1','h_2','h_3');axis([0 L 0 8]);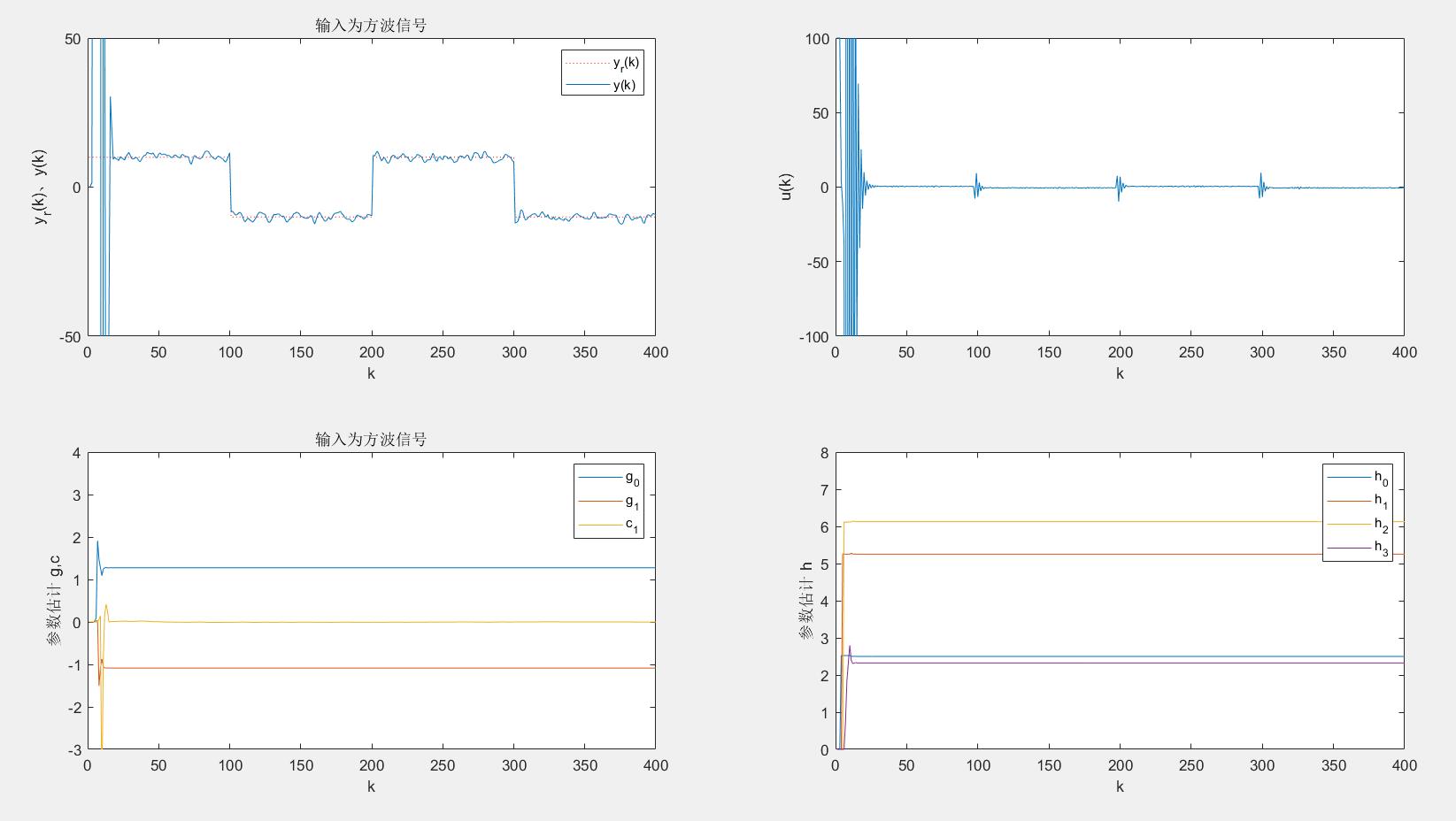 
(3) 被控对象模型修改后的：
①%幅值是10的阶跃信号
%#By 赶路人_87HZ 最小方差直接自校正控制 输入信号u(t)=%幅值是10的阶跃信号
clear all;close all;
a=[1 -1.5 0.7]; b=[0.5 1.5]; c=[1 0.5]; d=3; %对象参数
na=length(a)-1; nb=length(b)-1; nc=length(c)-1; %计算阶次
nh=nb+d-1; ng=na-1; %nh 为多项式 H 的阶次,ng 为多项式 G 的阶次
L=400;
uk=zeros(d+nh,1);
yk=zeros(d+ng,1);
yek=zeros(nc,1); %最优输出预测估计初值
yrk=zeros(nc,1);
xik=zeros(nc,1);
yr=10*[ones(L+d,1)]; %幅值是10的阶跃信号
xi=sqrt(0.1)*randn(L,1);%方差为 0.1 的白噪声序列
thetaek=zeros(na+nb+d+nc,d);
P=10^6*eye(na+nb+d+nc);
for k=1:L
time(k)=k;
y(k)=-a(2:na+1)*yk(1:na)+b*uk(d:d+nb)+c*[xi(k);xik];%采集输出数据
phie=[yk(d:d+ng);uk(d:d+nh);-yek(1:nc)];
K=P*phie/(1+phie'*P*phie);
thetae(:,k)=thetaek(:,1)+K*(y(k)-phie'*thetaek(:,1));
P=(eye(na+nb+d+nc)-K*phie')*P;
ye=phie'*thetaek(:,d);%预测输出估计值
%提取辨识参数
ge=thetae(1:ng+1,k)';
he=thetae(ng+2:ng+nh+2,k)';
ce=[1 thetae(ng+nh+3:ng+nh+nc+2,k)'];
if abs(ce(2))>0.9
ce(2)=sign(ce(2))*0.9;
end
if he(1)<0.1
he(1)=0.1;%设 h0 的下界为 0.1
end
uu=[yr(k+d:-1:k+d-min(d,nc))];
u(k)=(-he(2:nh+1)*uk(1:nh)+ce*[yr(k+d:-1:k+d-min(d,nc));yrk(1:nc-d)]-ge*[y(k);yk(1:na-1)])/he(1);%求控制量
%更新数据
for i=d:-1:2
thetaek(:,i)=thetaek(:,i-1);
end
thetaek(:,1)=thetae(:,k);
for i=d+nh:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=d+ng:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
for i=nc:-1:2
yek(i)=yek(i-1);
yrk(i)=yrk(i-1);
xik(i)=xik(i-1);
end
if nc>0
yek(1)=ye;
yrk(1)=yr(k);
xik(1)=xi(k);
end
end
%figure(1);
subplot(2,2,1);
plot(time,yr(1:L),'r:',time,y);
xlabel('k');ylabel('y_r(k)、y(k)');
legend('y_r(k)','y(k)');axis([0 L -100 100]);
title('输入为阶跃信号');%幅值是10的阶跃信号
subplot(2,2,2);
plot(time,u);
xlabel('k');ylabel('u(k)');axis([0 L -100 100]);
%figure(2);
subplot(2,2,3);
plot([1:L],thetae(1:ng+1,:),[1:L],thetae(ng+nh+3:ng+2+nh+nc,:));
xlabel('k');ylabel('参数估计 g,c');
legend('g_0','g_1','c_1');axis([0 L -3 4]);
title('输入为阶跃信号');
subplot(2,2,4);
plot([1:L],thetae(ng+2:ng+2+nh,:));
xlabel('k');ylabel('参数估计 h');
legend('h_0','h_1','h_2','h_3');axis([0 L 0 4]);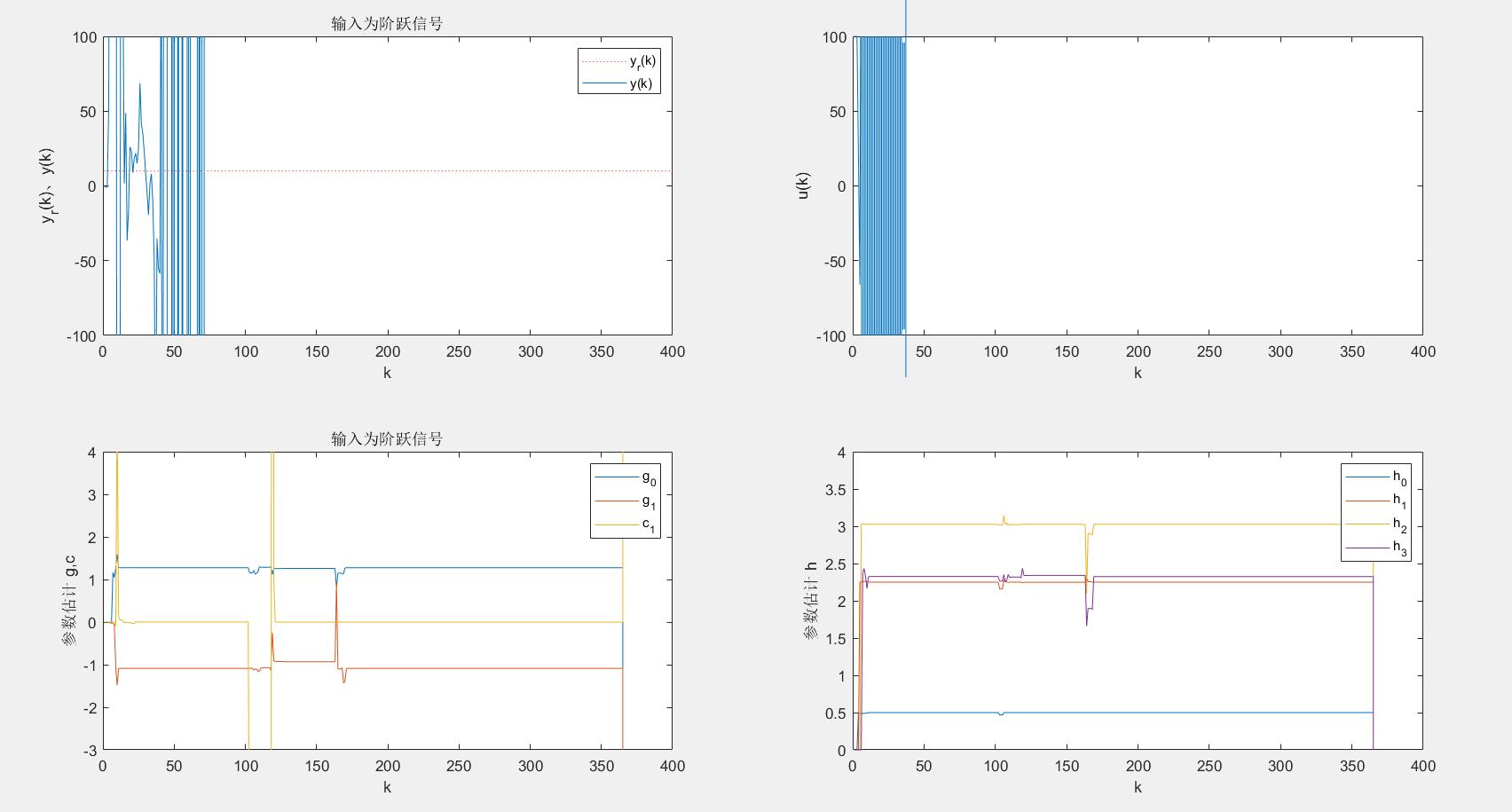 
②%幅值是10的方波信号
%#By 赶路人_87HZ 最小方差直接自校正控制 输入信号u(t)=%幅值是10的阶跃信号
clear all;close all;
a=[1 -1.5 0.7]; b=[0.5 1.5]; c=[1 0.5]; d=3; %对象参数
na=length(a)-1; nb=length(b)-1; nc=length(c)-1; %计算阶次
nh=nb+d-1; ng=na-1; %nh 为多项式 H 的阶次,ng 为多项式 G 的阶次
L=400;
uk=zeros(d+nh,1);
yk=zeros(d+ng,1);
yek=zeros(nc,1); %最优输出预测估计初值
yrk=zeros(nc,1);
xik=zeros(nc,1);
yr=10*[ones(L/4,1);-ones(L/4,1);ones(L/4,1);-ones(L/4+d,1)];% 期望输出 ②%幅值是10的方波信号
xi=sqrt(0.1)*randn(L,1);%方差为 0.1 的白噪声序列
thetaek=zeros(na+nb+d+nc,d);
P=10^6*eye(na+nb+d+nc);
for k=1:L
time(k)=k;
y(k)=-a(2:na+1)*yk(1:na)+b*uk(d:d+nb)+c*[xi(k);xik];%采集输出数据
phie=[yk(d:d+ng);uk(d:d+nh);-yek(1:nc)];
K=P*phie/(1+phie'*P*phie);
thetae(:,k)=thetaek(:,1)+K*(y(k)-phie'*thetaek(:,1));
P=(eye(na+nb+d+nc)-K*phie')*P;
ye=phie'*thetaek(:,d);%预测输出估计值
%提取辨识参数
ge=thetae(1:ng+1,k)';
he=thetae(ng+2:ng+nh+2,k)';
ce=[1 thetae(ng+nh+3:ng+nh+nc+2,k)'];
if abs(ce(2))>0.9
ce(2)=sign(ce(2))*0.9;
end
if he(1)<0.1
he(1)=0.1;%设 h0 的下界为 0.1
end
uu=[yr(k+d:-1:k+d-min(d,nc))];
u(k)=(-he(2:nh+1)*uk(1:nh)+ce*[yr(k+d:-1:k+d-min(d,nc));yrk(1:nc-d)]-ge*[y(k);yk(1:na-1)])/he(1);%求控制量
%更新数据
for i=d:-1:2
thetaek(:,i)=thetaek(:,i-1);
end
thetaek(:,1)=thetae(:,k);
for i=d+nh:-1:2
uk(i)=uk(i-1);
end
uk(1)=u(k);
for i=d+ng:-1:2
yk(i)=yk(i-1);
end
yk(1)=y(k);
for i=nc:-1:2
yek(i)=yek(i-1);
yrk(i)=yrk(i-1);
xik(i)=xik(i-1);
end
if nc>0
yek(1)=ye;
yrk(1)=yr(k);
xik(1)=xi(k);
end
end
%figure(1);
subplot(2,2,1);
plot(time,yr(1:L),'r:',time,y);
xlabel('k');ylabel('y_r(k)、y(k)');
legend('y_r(k)','y(k)');axis([0 L -100 100]);
title('输入为方波信号');%幅值是10的方波信号
subplot(2,2,2);
plot(time,u);
xlabel('k');ylabel('u(k)');axis([0 L -100 100]);
%figure(2);
subplot(2,2,3);
plot([1:L],thetae(1:ng+1,:),[1:L],thetae(ng+nh+3:ng+2+nh+nc,:));
xlabel('k');ylabel('参数估计 g,c');
legend('g_0','g_1','c_1');axis([0 L -3 4]);
title('输入为方波信号');
subplot(2,2,4);
plot([1:L],thetae(ng+2:ng+2+nh,:));
xlabel('k');ylabel('参数估计 h');
legend('h_0','h_1','h_2','h_3');axis([0 L 0 4]);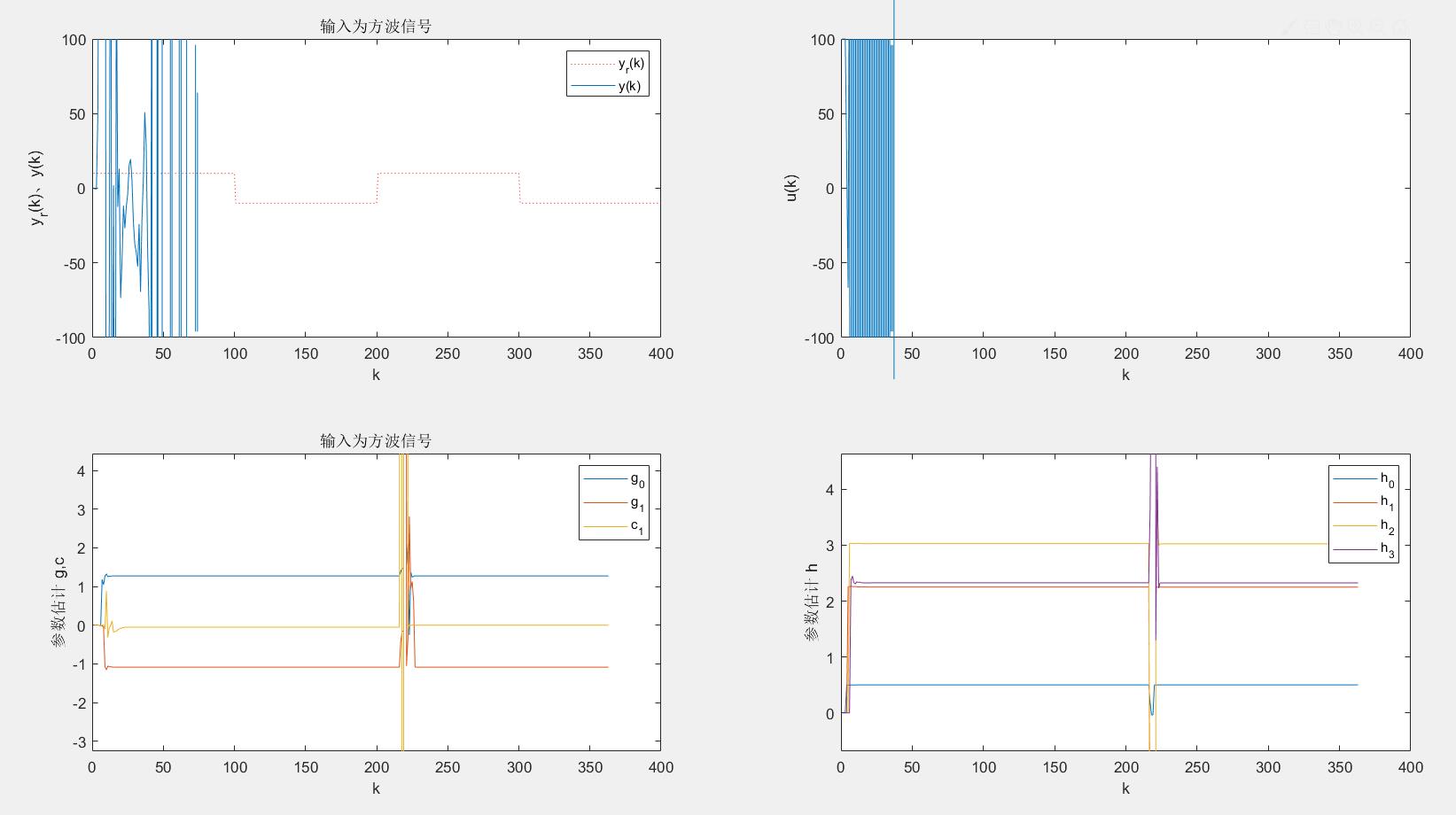 
作业三 模型参考自适应控制实验
设被控对象模型参数未知或慢时变，但其状态变量完全可观测，
仿真时取状态方程为：
选择参考模型：
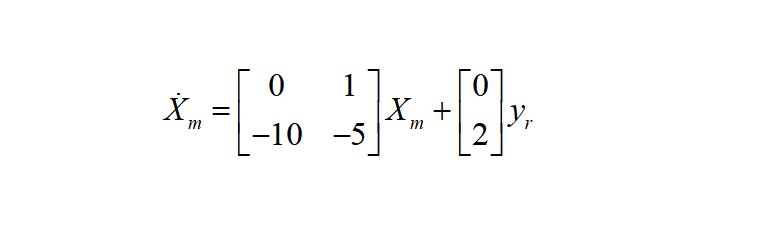
状态完全可观测的模型参考自适应控制系统如下图所示：
控制器自适应规律为：
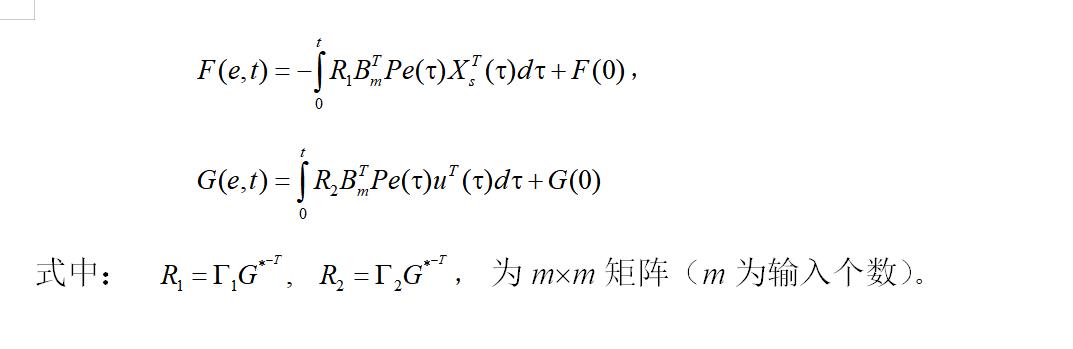
解：
%正定矩阵 取三组
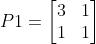
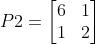
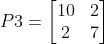
R1=1*eye(m); R2=1*eye(m); %自适应律参数矩阵 改前面的系数
【参考代码】
%#By 赶路人_87HZ 状态完全可测时，基于Lyapunov稳定性理论的MRAC
clear all; close all;
h=0.01; L=40/h; %数值积分步长和仿真步数
Ap=[0 1;-5 -3]; Bp=[0;6]; %对象参数
Am=[0 1;-10 -5]; Bm=[0;2]; %参考模型参数
Sz=size(Bp); n=Sz(1); m=Sz(2); %状态向量、输入维数
P=[3 1;1 1]; %正定矩阵 取三组
R1=1*eye(m); R2=1*eye(m); %自适应律参数矩阵 改前面的系数
F0=zeros(m,n); K0=zeros(m); %初值
yr0=zeros(m,1); u0=zeros(m,1); e0=zeros(n,1);
xp0=zeros(n,1); xm0=zeros(n,1);
for k=1:L
time(k)=k*h;
yr(k)=4*sin(0.2*pi*time(k)); %输入信号
xp(:,k)=xp0+h*(Ap*xp0+Bp*u0); %计算xp
xm(:,k)=xm0+h*(Am*xm0+Bm*yr0); %计算xm
e(:,k)=xm(:,k)-xp(:,k); %e=xm-xp
F=F0+h*(R1*Bm'*P*e0*xp0'); %自适应律
K=K0+h*(R2*Bm'*P*e0*yr0');
u(:,k)=K*yr(k)+F*xp(:,k); %控制量
parae(1,k)=norm(Am-Ap-Bp*F); %参数收敛于Am的偏差
parae(2,k)=norm(Bm-Bp*K); %参数收敛于Bm的偏差
%更新数据
yr0=yr(:,k); u0=u(:,k); e0=e(:,k);
xp0=xp(:,k); xm0=xm(:,k);
F0=F; K0=K;
end
figure(1);
subplot(2,1,1);
plot(time,xm(1,:),'r',time,xp(1,:),':');
xlabel('t'); ylabel('x_m_1(t)、x_p_1(t)');
legend('x_m_1(t)','x_p_1(t)');
subplot(2,1,2);
plot(time,xm(2,:),'r',time,xp(2,:),':');
xlabel('t'); ylabel('x_m_2(t)、x_p_2(t)');
legend('x_m_2(t)','x_p_2(t)');
figure(2);
plot(time,parae(1,:),':',time,parae(2,:),'r');
xlabel('t'); ylabel('参数收敛偏差E');
legend('||A_m-A_p-B_p*F||_2','||B_m-B_p*K||_2');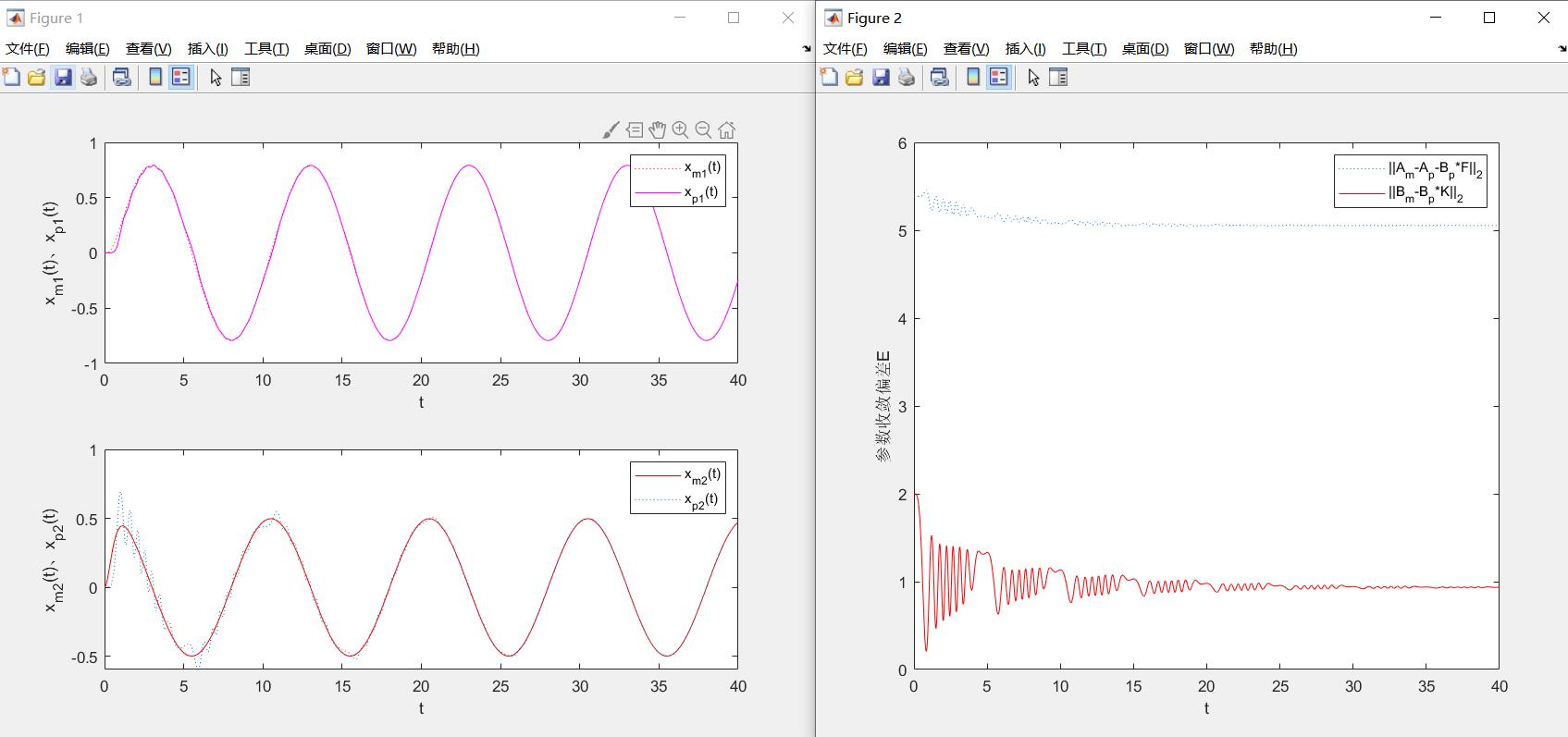
② 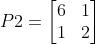R1=2*eye(m); R2=2*eye(m); %自适应律参数矩阵
%#By 赶路人_87HZ 状态完全可测时，基于Lyapunov稳定性理论的MRAC
clear all; close all;
h=0.01; L=40/h; %数值积分步长和仿真步数
Ap=[0 1;-5 -3]; Bp=[0;6]; %对象参数
Am=[0 1;-10 -5]; Bm=[0;2]; %参考模型参数
Sz=size(Bp); n=Sz(1); m=Sz(2); %状态向量、输入维数
P=[6 1;1 2]; %正定矩阵 取三组
R1=3*eye(m); R2=3*eye(m); %自适应律参数矩阵 改前面的系数
F0=zeros(m,n); K0=zeros(m); %初值
yr0=zeros(m,1); u0=zeros(m,1); e0=zeros(n,1);
xp0=zeros(n,1); xm0=zeros(n,1);
for k=1:L
time(k)=k*h;
yr(k)=4*sin(0.2*pi*time(k)); %输入信号
xp(:,k)=xp0+h*(Ap*xp0+Bp*u0); %计算xp
xm(:,k)=xm0+h*(Am*xm0+Bm*yr0); %计算xm
e(:,k)=xm(:,k)-xp(:,k); %e=xm-xp
F=F0+h*(R1*Bm'*P*e0*xp0'); %自适应律
K=K0+h*(R2*Bm'*P*e0*yr0');
u(:,k)=K*yr(k)+F*xp(:,k); %控制量
parae(1,k)=norm(Am-Ap-Bp*F); %参数收敛于Am的偏差
parae(2,k)=norm(Bm-Bp*K); %参数收敛于Bm的偏差
%更新数据
yr0=yr(:,k); u0=u(:,k); e0=e(:,k);
xp0=xp(:,k); xm0=xm(:,k);
F0=F; K0=K;
end
figure(1);
subplot(2,1,1);
plot(time,xm(1,:),'r',time,xp(1,:),':');
xlabel('t'); ylabel('x_m_1(t)、x_p_1(t)');
legend('x_m_1(t)','x_p_1(t)');
subplot(2,1,2);
plot(time,xm(2,:),'r',time,xp(2,:),':');
xlabel('t'); ylabel('x_m_2(t)、x_p_2(t)');
legend('x_m_2(t)','x_p_2(t)');
figure(2);
plot(time,parae(1,:),':',time,parae(2,:),'r');
xlabel('t'); ylabel('参数收敛偏差E');
legend('||A_m-A_p-B_p*F||_2','||B_m-B_p*K||_2');
③ 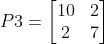R1=3*eye(m); R2=3*eye(m); %自适应律参数矩阵
%#By 赶路人_87HZ 状态完全可测时，基于Lyapunov稳定性理论的MRAC
clear all; close all;
h=0.01; L=40/h; %数值积分步长和仿真步数
Ap=[0 1;-5 -3]; Bp=[0;6]; %对象参数
Am=[0 1;-10 -5]; Bm=[0;2]; %参考模型参数
Sz=size(Bp); n=Sz(1); m=Sz(2); %状态向量、输入维数
P=[10 2;2 7]; %正定矩阵 取三组
R1=3*eye(m); R2=3*eye(m); %自适应律参数矩阵 改前面的系数
F0=zeros(m,n); K0=zeros(m); %初值
yr0=zeros(m,1); u0=zeros(m,1); e0=zeros(n,1);
xp0=zeros(n,1); xm0=zeros(n,1);
for k=1:L
time(k)=k*h;
yr(k)=4*sin(0.2*pi*time(k)); %输入信号
xp(:,k)=xp0+h*(Ap*xp0+Bp*u0); %计算xp
xm(:,k)=xm0+h*(Am*xm0+Bm*yr0); %计算xm
e(:,k)=xm(:,k)-xp(:,k); %e=xm-xp
F=F0+h*(R1*Bm'*P*e0*xp0'); %自适应律
K=K0+h*(R2*Bm'*P*e0*yr0');
u(:,k)=K*yr(k)+F*xp(:,k); %控制量
parae(1,k)=norm(Am-Ap-Bp*F); %参数收敛于Am的偏差
parae(2,k)=norm(Bm-Bp*K); %参数收敛于Bm的偏差
%更新数据
yr0=yr(:,k); u0=u(:,k); e0=e(:,k);
xp0=xp(:,k); xm0=xm(:,k);
F0=F; K0=K;
end
figure(1);
subplot(2,1,1);
plot(time,xm(1,:),'r',time,xp(1,:),':');
xlabel('t'); ylabel('x_m_1(t)、x_p_1(t)');
legend('x_m_1(t)','x_p_1(t)');
subplot(2,1,2);
plot(time,xm(2,:),'r',time,xp(2,:),':');
xlabel('t'); ylabel('x_m_2(t)、x_p_2(t)');
legend('x_m_2(t)','x_p_2(t)');
figure(2);
plot(time,parae(1,:),':',time,parae(2,:),'r');
xlabel('t'); ylabel('参数收敛偏差E');
legend('||A_m-A_p-B_p*F||_2','||B_m-B_p*K||_2');
以上是关于《系统辨识》作业CSU的主要内容，如果未能解决你的问题，请参考以下文章