美赛BOOM数学建模BOOM1-4多目标规划

Posted 2023-01-15 鸥小羊

❑模型简介

❑ 本质

既要XXX，又要XXX

❑ 回顾：(非)线性规划都是一个目标函数，例如工业生产产品，追求最大化利润等等。

❑ 例如：某工厂生产产品Ⅰ和产品Ⅱ，有关数据如下，若只追求最大化利润，得到模型：

❑ 多目标

现在设有3个目标：

• 1.尽量使产品Ⅰ的产量不超过产品Ⅱ的产量；

• 2.尽可能充分利用设备，但不希望加班

• 3.尽可能使利润不少于56万

❑ 翻译翻译

• 目标1是“不超过”，也就是尽量“⩽”

• 目标2是“充分利用又不加班”，也就是尽量“=”

• 目标3是“不少于”，也就是尽量“⩾”

• “尽可能”的意思是，能满足最好

• 若满足不了，就要在多个目标中做出取舍

• 隐藏条件：原材料有限，生产总消耗无法超出原材料

❑ 解题思路

• 需要衡量每个目标的完成情况；

• 如果三个目标有一定冲突，要在主观上区分三个目标的重要性；

• 使得整体的完成情况尽量好。

❑ 多目标规划难在哪？

• 极端例题：尽量保证每天吃的肉不少5斤，且尽可能保持体重在100斤以下

• “既要”“又要”，但有时难以同时满足所有目标

❑ 如何衡量每个目标的完成情况

• 正偏差变量为实际值超过目标值的部分，

• 负偏差变量为实际值未达到目标值的部分，（为整数）

• 第3个目标要求不少于目标值，意味着负偏差变量越小越好

❑ 约束必须满足么？

• 生产用的原材料用完了就没了，所以“原材料有限”为绝对约束，必须满足

• 有些目标例如尽可能使利润不少于56万，对追求的目标值允许有偏差，称为目标约束

❑ 目标太多，难以都满足，应该先满足谁？

• 多个目标可能难以同时满足，到底哪个更重要？需要确定优先因子

❑ 模型建立的基本原理：将目标约束转化为偏差变量表示的目标函数和等式约束

❑适用赛题

❑ 生产规划：

使XXX最少/多/利润最大，且尽可能XXX，尽量XXX，在…基础上优化XXX;

❑典型例题

❑ 某工厂生产产品Ⅰ和产品Ⅱ，有关数据如下，

• 1.尽量使产品Ⅰ的产量不超过产品Ⅱ的产量；

• 2.尽可能充分利用设备，但不希望加班

• 3.尽可能使利润不少于56万

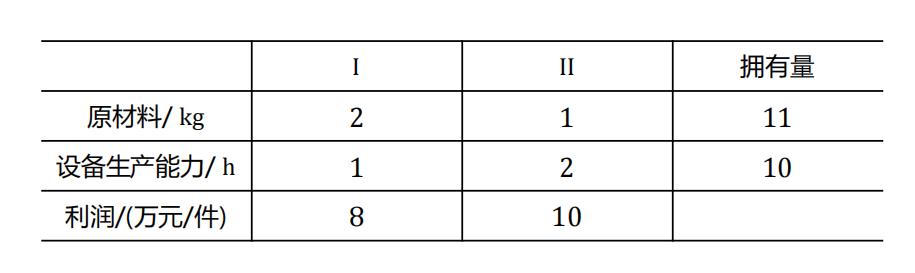
❑ 需要衡量每个目标的完成情况，并区分三个目标的重要性，使得整体的完成情况尽量好

• 引入三个概念：正负偏差变量，绝对约束和目标约束，优先因子

❑三个概念

❑ 概念一：正负偏差变量，衡量每个目标的完成情况

❑ 该目标是“尽可能使利润不少于56万”，超了好还是差了好？当然超了好！而且超再多也不怕

• 即正偏差变量是多少，都无所谓；

• 而该目标追求“尽量不少于”，意味着负偏差变量 越小越好

❑ 目标函数（根据偏差变量）

• 第1个目标要求不超过目标值，意味着正偏差变量 越小越好

• 利用优先因子，从题目要求的目标3中获得目标函数：

• 第3个目标要求不少于目标值，意味着负偏差变量越小越好

• 利用优先因子，从题目要求的目标3中获得目标函数：

❑ 第2个目标的子目标

• 第2个目标中其实包含两个子目标： “充分利用设备”和“不希望加班”

• 正偏差变量代表加班时间， 负偏差变量代表没有充分利用设备的时间

• “充分利用设备”意味着总生产时间不少于10，即⩾ 10

• “不希望加班”意味着总生产时间不大于10，即⩽ 10

• 同时满足这两条，就是对这两个子目标取交集，所以目标2写做： = 10

• 所以第2个目标要求等于目标值，意味着正负偏差都尽量小

• 利用优先因子，从题目要求的目标2中获得目标函数：

❑ 第2个目标细化

• 上一页中，目标函数min( + )是基于目标2中的两个子目标重要性相同的前提

• 现实中，“充分利用设备”和“不希望加班”还是存在重要性的差别

• 假如题目中提到“近期订单较多”之类的语句，那么“不希望加班”的重要性就较低

• 此时可给 和再分别赋权重，称为权系数，以区分重要性，例如目标函数改为：

• 意味着“不加班”的重要性较低，让步于“充分利用设备”

• 本课程例题不考虑该类情况，依旧使用min ( + )

• 补充：类似的情况，比如在销售时有“尽量把所有产品都卖完” 的目标，但不同产品利润不一样，现实中当然是先尽量把利润高的卖完，这种目标就可根据利润比来给同一个目标下的不同偏差变量设定权重

❑ 概念二：绝对约束和目标约束

• 绝对约束

是模型中自带的约束条件，必须满足，否则是不可行解

• 例如 ⩽ 11，使用材料的数量不能超过总量（总不能凭空变出来材料吧）

❑ 目标约束

是模型中对不等式右端追求的值允许有偏差

• 以目标3为例：尽可能使利润不少于56万，也就是𝑧 = ⩾ 56

• “尽可能”三个字意味着允许有偏差，也就是多于56或少于56都行

• “偏差”就是加入正负偏差变量，变成： 8+ 10+=56

• 利用正负偏差变量，从目标3中获得等式约束条件(加上不足的减去多余的)

❑ 利用实际值与目标值之间存在“偏差”，即正负偏差变量，多退少补

• 把目标函数中的不等式约束变成了等式约束

• 实际值加上未达到的部分、减去超过的部分，就等于目标值

❑ 概念三：优先因子

• 三个目标：1.尽量使产品Ⅰ的产量不超过产品Ⅱ的产量；2.尽可能充分利用设备，但不希望加

班； 3.尽可能使利润不少于56

• 这三者可能难以同时满足，到底哪个更重要？

• 例如，根据文献或题目要求等，目标1最重要，设最重要的目标的优先因子是p1

• 目标2第二重要，设其优先因子是p2

• 目标3第三重要，设其优先因子是p3

• 那么三个目标重要性就是目标1>目标2>目标3

• 注意：不同的求解方法下，优先因子的作用是不同的

• 序贯算法中，优先因子只是用来区分目标的相对重要性，不需要其具体数值

• 而在线性加权法中，需要确定具体数值（该方法过于简单、适用性小，不建议使用）

• 序贯算法的具体操作会在第四部分代码求解时讲解

❑ 总结

• 题目：某工厂生产产品Ⅰ和产品Ⅱ，有关数据如下，有3个目标：

• 1.尽量使产品Ⅰ的产量不超过产品Ⅱ的产量；

• 2.尽可能充分利用设备且不加班；

• 3.尽可能使利润不少于56万

❑ 解题基本步骤

• 根据目标约束写出等式约束条件；

• 根据正负偏差变量和优先因子，得到不同目标的目标函数；

• 别忘了题目还有绝对约束： ⩽ 11，因为生产材料有限

因为偏差中含有x所以目标函数中是含有x变量的，得出最后求解偏差的式子

❑代码求解

❑ 求解多目标规划

• 通用解法：

• 根据优先因子的先后次序，将问题分解成单目标规划

• 三个目标，每个目标都可视为单目标的线性规划

❑ 常用解法：序贯算法

• 根据模型中各个目标的优先级（优先因子），确定各目标的求解次序（尽量减少主观性不设置数值只设置p1，p2，p3等）

• 求第一级单目标规划的最优值记为

• 以第一级单目标等于最优值为新的约束，求第二级目标最优值，记为

• 依次递推，直到所有目标都求完，或不存在可行解为止

❑ 多目标规划还涉及帕累托解等概念，以后补充。

❑ 代码分析

❑ 求第一级目标（i=1）时

• 目标函数和约束条件，对于三个目标的偏差变量都没有约束

• 代码中用小于等于一个很大的数来表示。但既然说没有约束，那不写这三个约束不就行了么？

• 为的是后面有约束时只要更新不等式右边的数值即可，而不必增加新的约束，便于简化代码

❑ 求第二级目标（i=2）时

• 因为第一级求得最优值= 0 ，把该条作为新约束加入约束条件里

• 因为每一个目标都是最小化偏差变量，所以新加入的约束写作⩽ 0，等价于= 0

• 思考：为什么取“⩽”等价于“=”？既然等价，为什么不直接写= 0？

• 这样做是为了代码简洁统一，只要更新不等式右边的数值即可

• 此时的目标函数和约束条件：

❑ 求第三级目标（i=3）时

• 第二级求得最优解+= 0，把该条加入约束条件里

• 与上一页所讲的一样，同样以小于等于代替等于

• 此时的目标函数和约束条件：

❑ 求解结果

• 三级都求完了，迭代结束，求得满意解为 = 2, = 4。得数为整数，如果是小数可以使用整数规划，多加一个约束条件，向下取整以保证满足约束条件

• 在优先考虑尽量使产品Ⅰ产量不超过产品Ⅱ，其次尽可能充分利用设备且不加班，最后尽可能使利润不少于56万的情况下，应该安排每天生产2台设备Ⅰ，4台设备Ⅱ。

• 注意多目标规划求得的叫做“满意解”而不是“最优解”

• 多目标规划没有最优的概念

• 因为在求解过程中，三个目标的重要性的设定是具有主观性的，比赛时应尽量避免主观性

• 假如改变三个目标的重要性排序，那么求解结果也会变

本节课涉及的优化变量optimvar、优化问题optimproblem概念

MATLAB官方讲解：

https://ww2.mathworks.cn/help/optim/ug/optimvar.html

https://ww2.mathworks.cn/help/optim/ug/optim.problemdef.optimizationproblem.solve.html?searchHighlight=solve&s_tid=srchtitle_solve_2

当前模型：

❑ 代码实现

clc, clear
% 使用优化变量、优化问题来求解
% 创建优化变量x，dp和dm，类似于利用C++的类optimvar来创建对象x，dp，dm
% 可以用来为目标函数和问题约束创建表达式；optimvar是matlab自带的关键词，意思是要定义优化变量x（里外统一）
x = optimvar('x',2,'LowerBound',0);   % 定义两个变量x，最小值lowerbound（matlab自带关键词）都为0
dp = optimvar('dp',3,'LowerBound',0); % 定义3个正偏差变量dp，最小值都为0
dm = optimvar('dm',3,'LowerBound',0); % 定义3个负偏差变量dm，最小值都为0

% 创建求最小值的优化问题p；optimproblem（自带）创建优化类问题
p=optimproblem('ObjectiveSense','min'); %objectivesense表示设置的问题类型(一个属性)，本句表示求解问题的最小值
%还有其他属性，可自行查询

% 设置优化问题的约束条件
p.Constraints.cons1 = ( 2*x(1)+x(2)<=11 );  %constraints（关键词）表示约束条件；cons1为约束条件的第一条，也可表示第一次写入约束条件（可以写一条，也可以写多条，多条时换行即可，不需要加符号）
% 注意，表示相等关系用的符号是"=="
p.Constraints.cons2=[x(1)-x(2)+dm(1)-dp(1)==0       
                     x(1)+2*x(2)+dm(2)-dp(2)==10
                     8*x(1)+10*x(2)+dm(3)-dp(3)==56];

% 设置目标函数obj
obj=[dp(1); dm(2)+dp(2); dm(3)];
% 单级目标函数的最优值goal，初始设为足够大的数
% 非常宽松的约束就等于没有约束，确保第一级的正常运算
goal=100000*ones(3,1);  %三行一列的矩阵，每个数都是100000

for i=1:3
    % 重要：更新上一级的最优值，作为该级的约束条件;
    p.Constraints.cons3=[obj<=goal]; %增加一个新约束，<=在此处只有=的作用，有小于好处是在迭代中直接更改右边的数值，简化编程过程，而小于号无影响是因为上一级已经求出来的就是最优解
    p.Objective=obj(i);
    [sx,fval]=solve(p);     % 针对优化问题使用solve，会自动选择求解方式*****很好用
    fprintf('第%d级目标求解为：\\n',i)
    fval, xx=sx.x, sdm=sx.dm, sdp=sx.dp %sx.x表示最优解中x的数值，sx中还含有其他参数
    goal(i)=fval;  %更新迭代
end

代码中的solve()用来求解优化类问题，会自动判断问题类型并调用默认求解器

求每一级目标（i=1，2，3）时相应变化的约束条件见PPT

三级都求完了，迭代结束，求得满意解为。即应该安排每天生产2台设备Ⅰ，4台设备Ⅱ。

注意多目标规划求得的叫做“满意解”而不是“最优解”，多目标规划的最终解没有最优的概念。因为在求解过程中，三个目标的重要性的设定是具有主观性的，假如改变三个目标的重要性排序，那么求解结果也会变。