130. 被围绕的区域

Posted 2023-01-13 Debroon

130. 被围绕的区域

• • 题目
  • 算法设计：深度优先搜索
  • 算法设计：并查集

 

---

题目

 

---

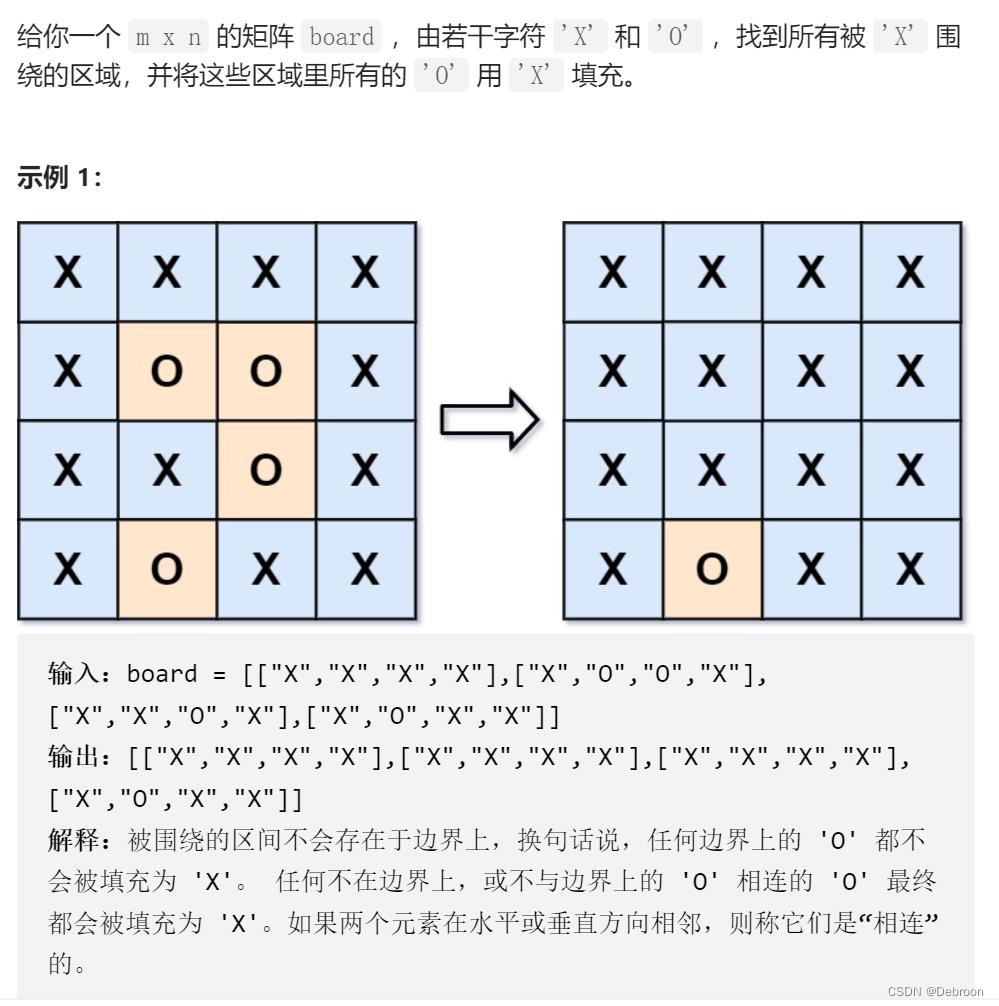
算法设计：深度优先搜索

如何在二维矩阵中使用 DFS 搜索呢？

如果你把二维矩阵中的每一个位置看做一个节点，这个节点的上下左右四个位置就是相邻节点，那么整个矩阵就可以抽象成一幅网状的图结构。

// 二维矩阵深度优先搜索框架
void dfs(int[][] grid, int i, int j, bool[][] visited) 
    int m = grid.length, n = grid[0].length;      // 二维矩阵的行数、列数
    if (i < 0 || j < 0 || i >= m || j >= n)       // 超出索引边界
        return;
    if (visited[i][j])                            // 已遍历过 (i, j)
        return;
    
    visited[i][j] = true;                         // 进入节点 (i, j)
    dfs(grid, i - 1, j, visited); 				  // 上
    dfs(grid, i + 1, j, visited); 				  // 下
    dfs(grid, i, j - 1, visited);     			  // 左
    dfs(grid, i, j + 1, visited); 			      // 右

 

---

DFS：先从边缘的 O 出发，遇到 O 就标记为 #，表示其与边界相连。然后遍历矩阵，遇到 # 置 O，遇到 O 置 X。

class Solution 
public:
    void solve(vector<vector<char>>& board) 
        if ( board.size() == 0 ) return;
        int m = board.size();        // 二维矩阵的行数
        int n = board[0].size();     // 二维矩阵的列数
        for (int i = 0; i < m; i++) 
            for (int j = 0; j < n; j++) 
                bool isEdge = i == 0 || j == 0 || i == m - 1 || j == n - 1; // 从边缘O开始搜索
                if (isEdge && board[i][j] == 'O') 
                    dfs(board, i, j); 
            
        for (int i = 0; i < m; i++) 
            for (int j = 0; j < n; j++) 
                if (board[i][j] == 'O')    // 与边界 O 不连通
                    board[i][j] = 'X';     
                if (board[i][j] == '#')    // 与边界 O 连通
                    board[i][j] = 'O';         
            
    

    void dfs(vector<vector<char>>& board, int i, int j) 
        if (i < 0 || j < 0 || i >= board.size()  || j >= board[0].size() || board[i][j] == 'X' || board[i][j] == '#') // ‘#’ 搜索过了
            return;  
        board[i][j] = '#';
        dfs(board, i - 1, j); // 上
        dfs(board, i + 1, j); // 下
        dfs(board, i, j - 1); // 左
        dfs(board, i, j + 1); // 右
    
;

 

---

算法设计：并查集

一些使用 DFS 深度优先算法解决的问题，也可以用 Union-Find 算法解决。

并查集常用来解决连通性的问题，即将一个图中连通的部分划分出来。当我们判断图中两个点之间是否存在路径时，就可以根据判断他们是否在一个连通区域。 而这道题我们其实求解的就是和边界的 O 在一个连通区域的的问题。

• 学习并查集，请猛击：https://blog.csdn.net/qq_41739364/article/details/121539887

并查集：将所有的 O 连通起来，并将边界的 O 与一个超级节点super连起来，最后遍历一遍遇到 O 判断是否跟超级节点是不是在一个集合里面，相连代表其与边界连通置 O，反之则代表其被包围，置X。

维持 m*n 为超级节点是关键 —— 在遍历时是从上到下，从左到右，于是在每格处只关注本格的左边和上边。

第一种情况，如果这两者有一个是超级节点，那么自身也加入。

第二种情况，如果两者都不是超级节点，将自身作为上、左两个格子指向的目标，形成一个独立小分队。

• 等到某位置，独立小分队被某个超级节点吸收，之前缓存的很多节点都会汇入超级节点
• 如果这支小分队到结束都还没找到超级节点，就被开除革命队伍了，全部O变为X。

class Solution 
	int super;                                             // 并查集的超级节点 
public:
    void solve(vector<vector<char>>& board) 
        if (board.empty()) return;
        int m = board.size(), n = board[0].size();         // 二维矩阵的行数、列数
        ufSet(m * n + 1);                                  // 初始化并查集，多开一个位置作为超级节点
        super = m * n;                                     // 超级节点的位置是行数m * 列数n
        for (int i = 0; i < m; ++i)                        // 从上往下遍历
            for (int j = 0; j < n; ++j)                   // 从左往右遍历
                if (board[i][j] == 'X') continue;
                if (!j || !i || i + 1 == m || j + 1 == n)  // 将第0行、第0列、最后一行、最后一列的边界节点 O 与 当前节点 连通，且根节点为超级节点
                    merge(super, i * n + j);               // 并查集是一维数组实现，题目是二维数组，二维转一维的映射关系：[i, j] -> i * n + j，把(i, j)的O与超级节点连通
                if (j > 0 && board[i][j - 1] == 'O')       // 遍历除第0列、最后一列的非边界节点 O
                    merge(i * n + j - 1, i * n + j);       // 如果上边是O，那么本格的O，与上边连通，是不是超级节点看上边的根节点
                if (i > 0 && board[i - 1][j] == 'O')       // 遍历除第0行、最后一行的非边界节点 O
                    merge((i - 1) * n + j, i * n + j);     // 如果左边是O，那么本格的O，与左边连通，是不是超级节点看左边的根节点
            
        for (int i = 0; i < m; ++i) 
            for (int j = 0; j < n; ++j) 
                if (board[i][j] == 'O' && find(i * n + j) != super)  // 通过 find 查看是否与超级节点相连
                    board[i][j] = 'X';     // 如果不相连，置O为X
    
        
private:
	vector<int> uf;             // 并查集
    void ufSet(int n)          // 初始化并查集
        uf.resize(n);
        for (int i = 0; i < n; ++i)
            uf[i] = i;
    
    int find(int p)            // 返回某个节点 x 的根节点
        return uf[p] == p ? p : uf[p] = find(uf[p]);
    
    void merge(int p, int q)   // 连通 p、q
        int p1 = find(p), q2 = find(q);
        p1 == uf.size() - 1 ? uf[q2] = p1 : uf[p1] = q2;  // uf.size()-1 为超级节点，如果 p 的根节点是超级节点，那么 q 的根节点也设置为超级节点（p、q连通且为超级节点），否则 p 的跟节点变为 q 的根节点（p、q连通但只是普通节点连接）
    
;