LQ0272 矩形运算计算几何

Posted 2023-01-09 海岛Blog

题目来源：蓝桥杯2012初赛 Java A组H题

题目描述
在编写图形界面软件的时候，经常会遇到处理两个矩形的关系。

如图 1 所示，矩形的交集指的是：两个矩形重叠区的矩形，当然也可能不存在（参看图 2 ）。两个矩形的并集指的是：能包含这两个矩形的最小矩形，它一定是存在的。

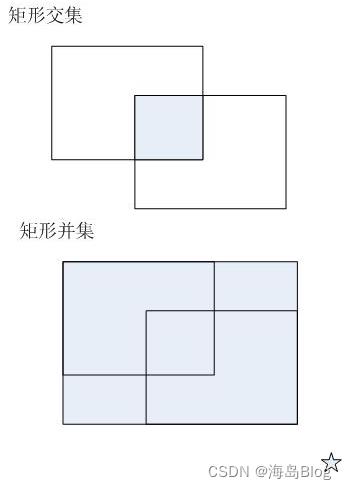
图 1

图 2

本题目的要求就是：由用户输入两个矩形的坐标，程序输出它们的交集和并集矩形。

矩形坐标的输入格式是输入两个对角点坐标，注意，不保证是哪个对角，也不保证顺序（你可以体会一下，在桌面上拖动鼠标拉矩形，4 个方向都可以的）。

输入描述
数据共两行，每行表示一个矩形。每行是两个点的坐标。x 坐标在左，y 坐标在右。坐标系统是：屏幕左上角为 (0,0)，x 坐标水平向右增大；y 坐标垂直向下增大。

输出描述
也是两行数据，分别表示交集和并集。如果交集不存在，则输出 NO。

前边两项是左上角的坐标。后边是矩形的长度和高度。

输入输出样例
示例
输入

100,220,300,100
150,150,300,300

输出

150,150,150,70
100,100,200,200

问题分析
注意，一个点重叠也算相交。

AC的C++语言程序如下：

/* LQ0272 矩形运算 */

#include <iostream>

using namespace std;

struct Point 
    int x, y;
;

int main()

    Point a, b, c, d;
    int x1, y1, x2, y2, x3, y3, x4, y4;
    scanf("%d,%d,%d,%d", &x1, &y1, &x2, &y2);
    scanf("%d,%d,%d,%d", &x3, &y3, &x4, &y4);

    a.x = min(x1, x2), a.y = min(y1, y2);
    b.x = max(x1, x2), b.y = max(y1, y2);
    c.x = min(x3, x4), c.y = min(y3, y4);
    d.x = max(x3, x4), d.y = max(y3, y4);

    bool flag = true;
    if (b.y < c.y || a.y > d.y || c.x > b.x || d.x < a.x) flag = false;
    int lx, ly, rx, ry;
    if (flag)  // 矩形相交
        // 交集
        lx = max(a.x, c.x), ly = max(a.y, c.y);
        rx = min(b.x, d.x), ry = min(b.y, d.y);
        printf("%d,%d,%d,%d\\n", lx, ly, (rx - lx), (ry - ly));

        // 并集
        lx = min(a.x, c.x), ly = min(a.y, c.y);
        rx = max(b.x, d.x), ry = max(b.y, d.y);
        printf("%d,%d,%d,%d\\n", lx, ly, (rx - lx), (ry - ly));
     else  // 矩形不相交
        cout << "NO" << endl;
        lx = min(a.x, c.x), ly = min(a.y, c.y);
        rx = max(b.x, d.x), ry = max(b.y, d.y);
        printf("%d,%d,%d,%d\\n", lx, ly, (rx - lx), (ry - ly));
    

    return 0;