图像基本知识整理——图像几何变换

Posted 2022-12-15 Lyndon_zheng

一、图像平移 图像平移是指将图像中的所有像素点按指定方向平移的一种变换。只改变图像在屏幕上的位置，图像本身不变。其实质是一种坐标变换。 1、基本原理 设图像中某点的原始坐标为(x0,y0)，平移量分别为Xset和Yset的距离，平移后的点为(x1,y1)，则平移后的坐标关系为： x1=x0+Xset
y1=y0+Yset
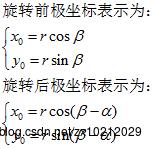
二、图像旋转 图像的旋转是图像校准，图像识别常用的一种技术。其本质是以图像的中心为原点，将图像上的所有的点都旋转相同的角度。 1、基本原理 设图像中某点的原始坐标为 (x0,y0)，旋转角度为a，旋转后的点为(x1,y1)，则平移后的坐标关系为：                   三、图像缩放 图像缩放是一种非常有用的图像处理方式，不管是在像素级别的处理，还是在高层特征提取等方面，多尺度对比的思想都有很重要的作用。 1、基本原理 设图像中某点的原始坐标为 (x0,y0)，缩放量分别为ZoomX和YoomY的距离，缩放后的点为(x1,y1)，则缩放后的坐标关系为：
x1=x0 *ZoomX
y1=y0 *ZoomY 四、插值算法 在实际操作中，缩放和旋转等几何变换会导致目标图像和原始像素点之间的关系不能相互对应，这时就需要运用插值算法来填补不能对应的点。在课程中，用到了最近邻插值、双线性插值和立方卷积插值。 1、最近邻插值 最近邻插值简单来说就是通过逆向运算得到一个浮点坐标，对浮点坐标进行取整后，在原图中找到与之相对应的像素作为目标像素。 算法实现：

for (i = 0; i<h_c - 1; i++)
	
		for (j = 0; j<w_c - 1; j++)
		
			int i0, j0;
			i0 = (int)(i / mmultiple + 0.5);
			j0 = (int)(j / mmultiple + 0.5);
			if ((i0 >= 0) && (i0<h) && (j0 >= 0) && (j0<w))
			
				::memcpy((unsigned char*)(lpDIBBitsNew + i*lineByte_c + j * 3), (unsigned char*)(lpDIBBits + i0*lineByte + j0 * 3), 3);//复制图像信息
			
			else
				::memset((unsigned char*)(lpDIBBitsNew + i*lineByte_c + j * 3), 255, 3);
		
	

其中i,j表示目标像素坐标点，i 0,j 0表示原图像像素的坐标。 最近邻算法的优点是思想直观，实现简单，但是得到的目标图像会出现模糊，图像的质量不高。
2、双线性插值 双线性插值算法是根据输出图像的宽度和高度将输入图像的宽度和高度进行均分，进而确定输出图像值的方法。 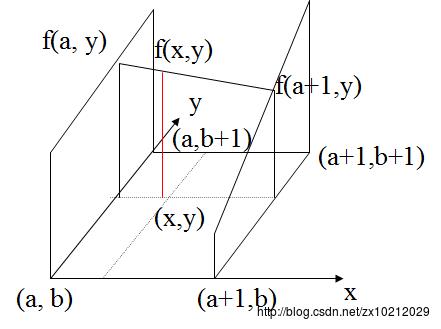其中(x,y)为目标图像坐标，(a,b)为原始图像坐标，f(x,y)表示该点的像素值。 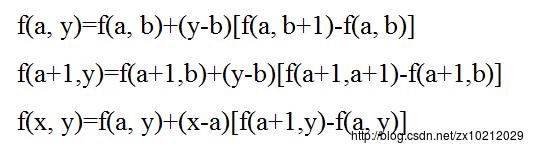算法实现：

for (i = 0; i<h_c - 1; i++)
	
		for (j = 0; j<w_c - 1; j++)
		
			i0 = (int)(i / mmultiple + 0.5);								
			j0 = (int)(j / mmultiple + 0.5);
			s1 = (i / 2.0 - i0)*(j / 2.0 - j0);
			s2 = (1.0 - i / 2.0 + i0)*(j / 2.0 - j0);
			s3 = (1.0 - i / 2.0 + i0)*(1.0 - j / 2.0 + j0);
			s4 = (i / 2.0 - i0)*(1.0 - j / 2.0 + j0);
			if ((i0 >= 0) && (i0<h) && (j0 >= 0) && (j0<w))
			
				*(lpDIBBitsNew + i*lineByte_c + j * 3) = char(s1**(lpDIBBits + i0*lineByte + j0 * 3) + s2**(lpDIBBits + i0*lineByte + (j0 + 1) * 3)
					+ s3**(lpDIBBits + (i0 + 1)*lineByte + j0 * 3) + s4**(lpDIBBits + (i0 + 1)*lineByte + (j0 + 1) * 3));
				*(lpDIBBitsNew + i*lineByte_c + j * 3 + 1) = char(s1**(lpDIBBits + i0*lineByte + j0 * 3 + 1) + s2**(lpDIBBits + i0*lineByte + (j0 + 1) * 3 + 1)
					+ s3**(lpDIBBits + (i0 + 1)*lineByte + j0 * 3 + 1) + s4**(lpDIBBits + (i0 + 1)*lineByte + (j0 + 1) * 3 + 1));
				*(lpDIBBitsNew + i*lineByte_c + j * 3 + 2) = char(s1**(lpDIBBits + i0*lineByte + j0 * 3 + 2) + s2**(lpDIBBits + i0*lineByte + (j0 + 1) * 3 + 2)
					+ s3**(lpDIBBits + (i0 + 1)*lineByte + j0 * 3 + 2) + s4**(lpDIBBits + (i0 + 1)*lineByte + (j0 + 1) * 3 + 2));
			
			else
				::memset((unsigned char*)(lpDIBBitsNew + i*lineByte_c + j * 3), 255, 3);
		
	

双线性插值后的图像质量提高，不会出现像素不连续的情况，但是计算量很大，且具有低通滤波器的性质，会使高频分量受损，最后可能导致图像的轮廓受损。 3、三次立方卷积插值 三次立方卷积是通过插值函数进行插值运算的。 双三次插值能够克服最近邻和双线性的不足，提高图像的质量。但是其计算量很大，对于大型图像处理就显得比较冗余。

其中w为插值逼近函数。

算法实现：

for (i = 0; i<h_c - 1; i++)
	
		for (j = 0; j<w_c - 1; j++)
		
			x = i / mmultiple; y = j / mmultiple; Ix = (int)x; Iy = (int)y; u = x - Ix; v = y - Iy;
			A[0] = w_f(1 + u); A[1] = w_f(u); A[2] = w_f(1 - u); A[3] = w_f(2 - u);
			C[0] = w_f(1 + v); C[1] = w_f(v); C[2] = w_f(1 - v); C[3] = w_f(2 - v);
			for (k = 0; k<3; k++)
			
				if ((Ix >= 0) && (Ix<h) && (Iy >= 0) && (Iy<w))
				
					B[0][0] = *(lpDIBBits + (Ix - 1)*lineByte + (Iy - 1) * 3 + k);  B[0][1] = *(lpDIBBits + (Ix - 1)*lineByte + (Iy)* 3 + k); 
					B[0][2] = *(lpDIBBits + (Ix - 1)*lineByte + (Iy + 1) * 3 + k);  B[0][3] = *(lpDIBBits + (Ix - 1)*lineByte + (Iy + 2) * 3 + k);
					B[1][0] = *(lpDIBBits + (Ix)*lineByte + (Iy - 1) * 3 + k);    B[1][1] = *(lpDIBBits + (Ix)*lineByte + (Iy)* 3 + k);   
					B[1][2] = *(lpDIBBits + (Ix)*lineByte + (Iy + 1) * 3 + k);    B[1][3] = *(lpDIBBits + (Ix)*lineByte + (Iy + 2) * 3 + k);
					B[2][0] = *(lpDIBBits + (Ix + 1)*lineByte + (Iy - 1) * 3 + k);  B[2][1] = *(lpDIBBits + (Ix + 1)*lineByte + (Iy)* 3 + k); 
					B[2][2] = *(lpDIBBits + (Ix + 1)*lineByte + (Iy + 1) * 3 + k);  B[2][3] = *(lpDIBBits + (Ix + 1)*lineByte + (Iy + 2) * 3 + k);
					B[3][0] = *(lpDIBBits + (Ix + 2)*lineByte + (Iy - 1) * 3 + k);  B[3][1] = *(lpDIBBits + (Ix + 2)*lineByte + (Iy)* 3 + k); 
					B[3][2] = *(lpDIBBits + (Ix + 2)*lineByte + (Iy + 1) * 3 + k);  B[3][3] = *(lpDIBBits + (Ix + 2)*lineByte + (Iy + 2) * 3 + k);

					for (i1 = 0; i1<4; i1++)
						M[i1] = 0;
					for (i1 = 0; i1<4; i1++)
					
						for (j1 = 0; j1<4; j1++)
						
							M[i1] += A[j1] * B[j1][i1];
						
					
					middle = 0;
					for (i1 = 0; i1<4; i1++)
						middle += M[i1] * C[i1];
					*(lpDIBBitsNew + i*lineByte_c + j * 3 + k) = (int)(middle + 0.5);
					if (*(lpDIBBitsNew + i*lineByte_c + j * 3 + k) > 255)
						*(lpDIBBitsNew + i*lineByte_c + j * 3 + k) = 255;
					if (*(lpDIBBitsNew + i*lineByte_c + j * 3 + k) < 0)
						*(lpDIBBitsNew + i*lineByte_c + j * 3 + k) = 0;
				
				else
					*(lpDIBBitsNew + i*lineByte_c + j * 3 + k) = *(lpDIBBits + (int)(i / 2.0 + 0.5)*lineByte + (int)(j / 2.0 + 0.5) * 3 + k);
			
		
	

几何变化效果图：


通过效果图我们可以看到，近临插值有不连续的地方，而双线性插值在边缘较多的地方会形成模糊，使边缘信息丢失。三次立方卷积的效果比较好，但是在实际计算时比较费时。