数据结构和算法LeetCode，初级算法-买卖股票的最佳时机 II

Posted 2022-12-14 数据结构和算法

截止到目前我已经写了 600多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

视频分析

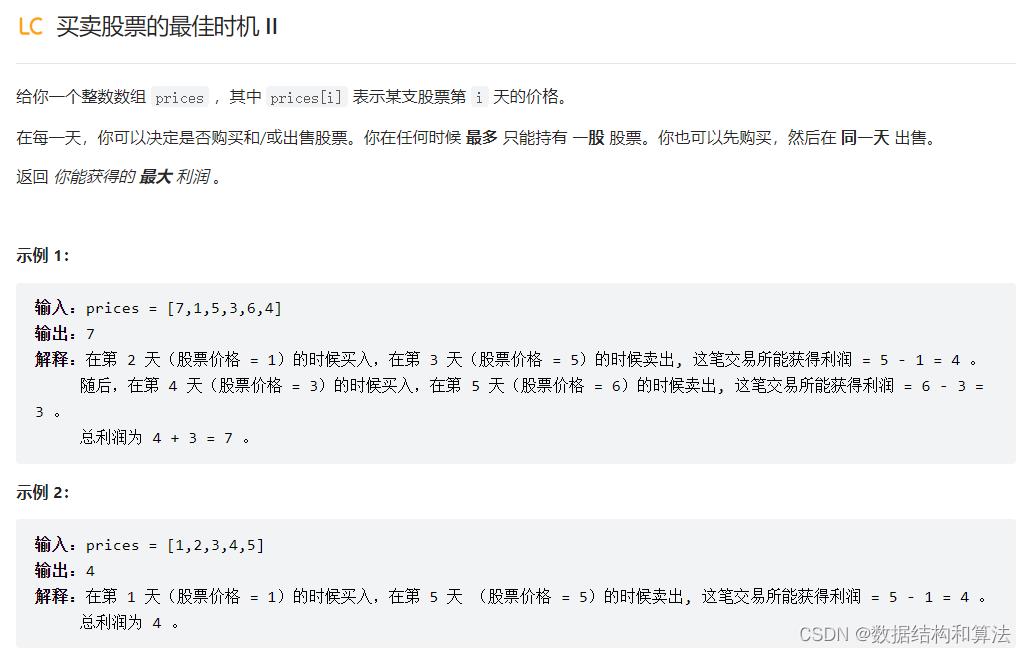
【数据结构和算法】初级算法-买卖股票的最佳时机 II

B站视频合集：https://www.bilibili.com/video/BV1uY4y1L76h/

代码部分

1，动态规划

java

public int maxProfit(int[] prices) 
    int length = prices.length;
    int[][] dp = new int[length][2];
    //初始条件
    dp[0][1] = -prices[0];
    for (int i = 1; i < length; i++) 
        //递推公式
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
    
    //最后一天肯定是手里没有股票的时候，利润才会最大，
    //只需要返回dp[length - 1][0]即可
    return dp[length - 1][0];

C++

public:
    int maxProfit(vector<int>& prices) 
        int length = prices.size();
        int dp[length][2];
        //初始条件
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for (int i = 1; i < length; i++) 
            //递推公式
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        
        //最后一天肯定是手里没有股票的时候，利润才会最大，
        //只需要返回dp[length - 1][0]即可
        return dp[length - 1][0];
    

python

    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        # dp[[0]*2]*n 
        dp = [[0]*2 for _ in range(length)]
         # 初始条件
        dp[0][1] = -prices[0]
        for i in range(1,length):
            # 递推公式
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])
        # 最后一天肯定是手里没有股票的时候，利润才会最大，
        # 只需要返回dp[length - 1][0]即可
        return dp[length - 1][0];

javascript

var maxProfit = function(prices) 
    let length = prices.length;
    let dp = Array.from(Array(length), () => new Array(2));
    dp[0][0] = 0;
    dp[0][1] = -prices[0];
    for (let i = 1; i < length; i++) 
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
    
    return dp[length - 1][0];
;

go

func maxProfit(prices []int) int 
    length := len(prices)
    dp := make([][2]int, length)
    dp[0][1] = -prices[0]
    for i := 1; i < length; i++ 
        dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
        dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
    
    return dp[length-1][0]


func max(a, b int) int 
    if a > b 
        return a
    
    return b

2，动态规划代码优化

public int maxProfit(int[] prices) 
    if (prices == null || prices.length < 2)
        return 0;
    int length = prices.length;
    //初始条件
    int hold = -prices[0];//持有股票
    int noHold = 0;//没持有股票
    for (int i = 1; i < length; i++) 
        //递推公式转化的
        noHold = Math.max(noHold, hold + prices[i]);
        hold = Math.max(hold, noHold - prices[i]);
    
    //最后一天肯定是手里没有股票的时候利润才会最大，
    //所以这里返回的是noHold
    return noHold;

3，贪心算法

java

public int maxProfit(int[] prices) 
    int total = 0, index = 0, length = prices.length;
    while (index < length) 
        //如果股票下跌就一直找，直到找到股票开始上涨为止
        while (index < length - 1 && prices[index] >= prices[index + 1])
            index++;
        //股票上涨开始的值，也就是这段时间上涨的最小值
        int min = prices[index];
        //一直找到股票上涨的最大值为止
        while (index < length - 1 && prices[index] <= prices[index + 1])
            index++;
        //计算这段上涨时间的差值，然后累加
        total += prices[index++] - min;
    
    return total;

C++

public:
    int maxProfit(vector<int>& prices) 
        int total = 0, index = 0, length = prices.size();
        while (index < length) 
            //如果股票下跌就一直找，直到找到股票开始上涨为止
            while (index < length - 1 && prices[index] >= prices[index + 1])
                index++;
            //股票上涨开始的值，也就是这段时间上涨的最小值
            int min = prices[index];
            //一直找到股票上涨的最大值为止
            while (index < length - 1 && prices[index] <= prices[index + 1])
                index++;
            //计算这段上涨时间的差值，然后累加
            total += prices[index++] - min;
        
        return total;
    

python

    def maxProfit(self, prices: List[int]) -> int:
        total, index, length = 0, 0, len(prices)
        while (index < length) :
            # 如果股票下跌就一直找，直到找到股票开始上涨为止
            while (index < length - 1 and prices[index] >= prices[index + 1]):
                index+=1
            # 股票上涨开始的值，也就是这段时间上涨的最小值
            min = prices[index]
            # 一直找到股票上涨的最大值为止
            while (index < length - 1 and prices[index] <= prices[index + 1]):
               index+=1
            # 计算这段上涨时间的差值，然后累加
            total += prices[index] - min
            index+=1
        return total

JavaScript

var maxProfit = function(prices) 
    let total = 0, index = 0, length = prices.length;
    while (index < length) 
        //如果股票下跌就一直找，直到找到股票开始上涨为止
        while (index < length - 1 && prices[index] >= prices[index + 1])
            index++;
        //股票上涨开始的值，也就是这段时间上涨的最小值
        let min = prices[index];
        //一直找到股票上涨的最大值为止
        while (index < length - 1 && prices[index] <= prices[index + 1])
            index++;
        //计算这段上涨时间的差值，然后累加
        total += prices[index++] - min;
    
    return total;
;

go

func maxProfit(prices []int) int 
    total := 0
    length := len(prices)
    index :=0
    for index < length 
        //如果股票下跌就一直找，直到找到股票开始上涨为止
        for index < length - 1 && prices[index] >= prices[index + 1]
 			index++;
        
        //股票上涨开始的值，也就是这段时间上涨的最小值
        min :=prices[index]
        //一直找到股票上涨的最大值为止
        for index < length - 1 && prices[index] <= prices[index + 1]
 			index++;
        
		//计算这段上涨时间的差值，然后累加
        total += prices[index] - min
        index++
    
    return total;
;

4，贪心算法代码优化

java

public int maxProfit(int[] prices) 
    int total = 0;
    for (int i = 0; i < prices.length - 1; i++) 
        //原数组中如果后一个减去前一个是正数，说明是上涨的，
        //我们就要累加，否则就不累加
        total += Math.max(prices[i + 1] - prices[i], 0);
    
    return total;

C++

public:
    int maxProfit(vector<int>& prices) 
        int total = 0;
        for (int i = 0; i < prices.size() - 1; i++) 
            //原数组中如果后一个减去前一个是正数，说明是上涨的，
            //我们就要累加，否则就不累加
            total += max(prices[i + 1] - prices[i], 0);
        
        return total;
    

Python

    def maxProfit(self, prices: List[int]) -> int:
        total = 0
        for i in range(len(prices)-1):
             total += max(prices[i + 1] - prices[i], 0);
        return total

JavaScript

var maxProfit = function(prices) 
    let total = 0
    for (let i = 0; i < prices.length - 1; i++) 
        total += Math.max(prices[i + 1] - prices[i], 0);
    
    return total;    
;

go

func maxProfit(prices []int) int 
    total := 0
    for i := 0; i < len(prices)-1 ; i++ 
       total += max(prices[i + 1] - prices[i], 0);
    
    return total


func max(a, b int) int 
    if a > b 
        return a
    
    return b