编程珠玑 第三部分 应用

Posted 2022-12-14 zhangqixiang5449

11.排序

这章介绍了插入排序和快速排序，这些知识都已经学过了，不在此重复。

---

12.取样问题

本章主要介绍了生成0~n-1区间内m个随机数并按序输出的三种方法。
方法一O(n)：
考虑m=2;n=5的情况，选择第一个数0的概率是2/5,但是选择数1的概率并不能是2/5，因为这样的选择方式可能选出的数个数不是m，因此要修改策略。在已经选择了0的情况下选择1的概率是1/4，未选择0的情况下选择1的概率是2/4。即要从r个剩余的整数中选出s个，我们以 s/r 的概率选择下一个数。

void genknuth(int m, int n)
    for(int i = 0; i < n; i++)
        if( ( rand() % (n-i) ) < m )//概率为 s/r
            cout<< i <<endl;
            m--;
        
    

方法2 O(mlogn):
用一个set储存结果。生成一个范围为0至(n-1)大小的整数，若set中没有这个数则插入set中。当set中元素为m个时，将set中元素排序输出。

方法3 O(n+mlogn)：
打乱一个包含整数0至(n-1)的数组顺序打乱，取前m个元素

void genshuf(int m ,int n)
    int i,j;
    int *x = new int[n];
    for(i = 0; i < n; i++)
        x[i] = i;
    
    for(i = 0; i < m; i++)
        j = randint(i,n-1);
        swap(x[i],x[j]);//展开swap可获得效率提升
    
    //排序x前m个元素，输出;

---

13.搜索

延续上一章生成0~n-1区间内m个随机数的问题，我们需要使用一种数据结构存储和处理生成的随机数（set），如排序、去重复等操作。
本章介绍了5中实现set的方案：有序数组、有序链表、二叉树、箱、位向量。各自性能如下：

集合表示	初始化操作	insert操作	输出操作	总时间	空 间
有序数组	1	m	m	O(m^2)	m
有序链表	1	m	m	O(m^2)	2m
二叉树	1	logm	m	O(mlogm)	3m
箱	m	1	m	O(m)	3m
位向量	n	1	n	O(n)	n/b

---

14.堆

堆可以解释为特殊的二叉树,其特殊性包括
1.顺序，任何根节点的值都小于或等于其子节点的值。
2.形状，如果有n个节点，那么所有节点到根节点距离都不超过log2n。即树种不应有空闲的位置，底层叶节点尽可能的靠左。
用数组实现的方法:

放置新元素的方法:先放入底部，在尽可能的向上递推。
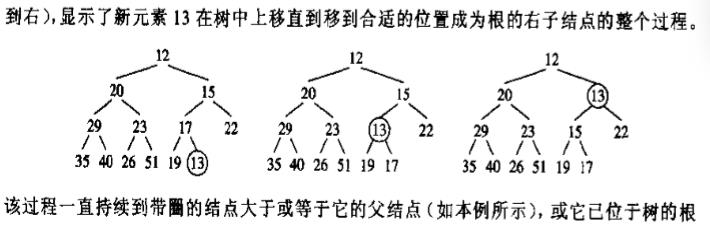
下图显示新元素13计入的方法。

删除的方法:与放入新元素的方法相反:如下图

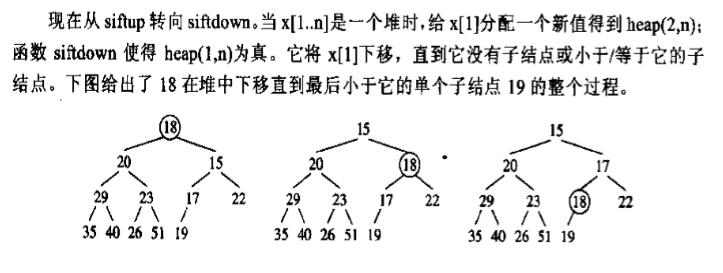
用堆来实现优先队列可较使用有序序列和无需序列实现带来折中并更好的各项性能

数据结构	一次insert	一次extractmin	两种操作各n次
有序数组	O(n)	1	O(n^2)
有序链表	O(log2n)	O(log2n)	O(nlog2n)
二叉树	1	O(n)	O(n^2)

使用优先级队列来排序:
插入待排序元素，然后删除。时间复杂度O(nlog2n)，需要额外使用堆所需的内存。

堆排序:
堆排序解决了优先级队列排序需要而外内存的负担。

//建堆
for i = [2 , n)  
  siftup(i)  

//排序
for( i = n ; i >= 2 ; i-- )  
  swap( l , i )  
  siftdown(i-1)

---

15.字符串

本章主要介绍了三种字符串的应用：

1、生成词典，统计单词的个数。
方案1和2使用了STL的set和map，其实本质是平衡搜索树。
方案3实现使用的是散列表，比方案1，2速度更快。

2、最长重复字串，用后缀数组实现。

3、生成随机文本。