机器学习系列(22)_SVM碎碎念part5：凸函数与优化

Posted 2022-12-13 寒小阳

原文地址：SVM - Understanding the math - convex-functions/ by Brandon Amos
感谢参与翻译同学：@程亚雄 && @张蒙 && @jozee
时间：2018年1月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/70214565
声明：版权所有，转载请联系寒小阳 ([e-mail])并注明出

1.引言

这是SVM数学基础系列教程第5部分。现在我们来学习凸函数相关的知识。如果你没有读过之前的文章，建议从《第一部分》开始学习。

1.1 如何找到全局最小值

有一种简单的方法可以找到全局最小值：

1. 找到所有的局部极小值
2. 最小的局部极小值就是全局最小值

还有另一种方法就是研究需要极小化的目标函数。如果这个函数是凸函数，那么就可以确保该函数的局部极小值即是全局最小值

定理：凸函数的局部极小值就是全局最小值 (Proof page 9)

2.凸函数

2.1 什么是凸函数

判断凸函数的条件是函数上的任意两点之间的线段与函数没有交点。

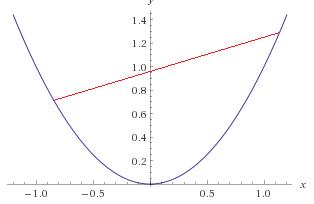
$$凸函数$$

然而，如果有交点，那么该函数就不是凸函数。

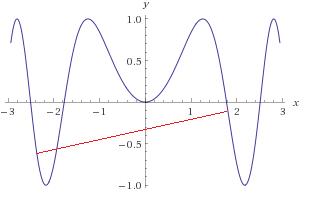
$$非凸函数$$

正如上图所示，函数两点之间的红色线段与函数曲线存在交点，这就意味着该函数是非凸函数。但是，请注意，上图中在某些特定的区间内，函数是满足凸函数条件，比如：区间[-1,+1]。

你可以在这里了解关于凸函数更加严谨的定义。但是当前最重要的是理解凸函数的局部极小值就是全局最小值。这有助于我们更加容易的求出凸函数的全局最小值。

通常，如果函数$-f$是凸函数，那么$f$就是凹函数。

$$凹函数$$

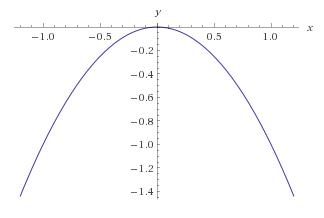
原先对于凸函数的定义同样适用于凹函数。即函数上的任意两点之间的线段与函数没有交点，那么该函数为凹函数。。。

因此，数学家们给出了凸函数更加严格的定义：

凸函数判定条件修正为如果函数上镜图（epigraph）（函数曲线上的点和函数曲线上方所有的点的集合）是凸集，那么该函数就是凸函数

2.2 什么是凸集

在欧几里得空间中，凸集表示一个区域，区域内任意两个点之间的线段都包含在该区域内。（维基百科）

同理可证，如果任取集合中的两个点，两点之间的线段包含在该集合中，那么该集合为凸集。

$$哪个集合是凸集，哪个是凹集？$$

圆和三角形是凸集，你猜对了吗？在下图中分别画出三条红色线段。正如你所看到的，五角星图形中的红色线段有一部分并不包含在五角星里面，这就表明它不是凸集。

$$五角星不是凸集$$

现在利用前面学到的知识来判断一个函数是不是凸函数。

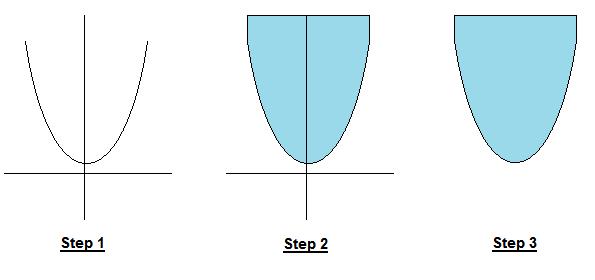
步骤一：我们有一个函数并且想要知道它是否是凸函数

步骤二：获取函数上镜图（把函数想象成一个U型容器，往里面灌水而且水不能溢出，一直加水直至到达容器的最高点，也就是函数极限）

步骤三：如果函数上镜图是凸的，那么该函数就是凸函数

2.3 如何判断函数为凸函数

通过函数上镜图可以很容易的判定该函数是否为凸函数，但是多元函数很难可视化。因此需要进一步研究凸函数的性质：

更一般地，一个连续的二阶可导多元函数在凸集上为凸函数，当且仅当函数的海森矩阵半正定。（维基百科）

如果想判定一个函数是否为凸函数，一种简单的方法就是使用海森矩阵(Hessian)。然而，这次我们不需要像前面的文章检查Hessian矩阵是否是正定矩阵，只需要检查它是否是半正定的。

两者的区别在哪？

定理：

以下的表述是等价的：

• 对称矩阵$A$ 是半正定矩阵

• 矩阵$A$ 的特征值为非负值

• 矩阵$A$ 的所有主子式非负

• 存在矩阵$B$ 使得$A=B^TB$

  （资料来源）

采用第4部分中的判定方法，使用子式来判断函数的海森矩阵是否为半正定。判定半正定和正定的区别在于，判定矩阵是否为半正定，需要检查所有的主子式，而不仅仅是顺序主子式 。同时，所有的主子式都必须是非负的。（大于0的数为正数；大于或者等于0的数为非负数）

2.3.1 举例：香蕉函数是凸函数吗？

香蕉函数的海森矩阵如下所示：

$$∇^2f(x,y)= \\left\\\\beginmatrix1200x^2-400y+2 & -400x \\\\\\ -400x & 200 \\endmatrix\\right\\ $$

海森矩阵的1阶主子式为：

$M11$ 等于$200$ (删除第一行和第一列)。

$M22$ 等于 $1200x^2 - 400y + 2$ (删除第二行和第二列)。

如果函数为凸函数，那么函数的海森矩阵的所有主子式在凸集内都是非负的。哪个凸集？根据定义，这里的凸集指的是凸函数的定义域。在这篇文章中，当我们说某个函数在凸集上为凸函数，这里的凸集均指函数定义域。限制条件”在凸集内”表示集合区域的边缘上的点不在选取范围内。

在这个例子中，函数定义域为$ℝ^2$ (凸集)。接下来，只需要证明在$ℝ^2$ 集合内任取一个点，都能使所有的主子式为非负的。

我们可以看到，子式$M11$ 始终为正数。但是，很容易找到一个点，使得$M22$为负数。比如$(1,4)$ 这个点。

结论：香蕉(banana)函数不是凸函数。

还有很多方法可以判定函数是否为凸函数。更多相关阅读，请参考这篇论文，part 2.1。

3.为什么凸函数如此完美

首先，凸函数的局部极小值就是全局最小值。这是一个非常好的结论可以帮助我们快速找到问题的解。

此外，一般情况下，凸优化问题更容易求解。为什么？

下图可以帮助我们更好的理解这个问题。

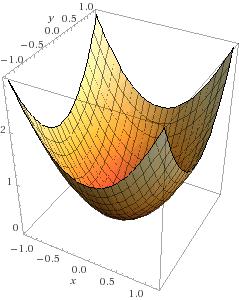
$$凸曲面$$

把求解最优化问题想象成往一个曲面上扔一颗弹珠。这里的曲面为凸曲面，如上图所示，不论那颗弹珠落在曲面上的哪一个点，它最终都会自己滚到曲面的最低点处，也就是函数取最小值的那个点。

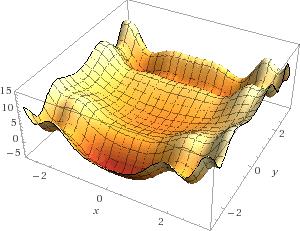
$$非凸曲面$$

那么非凸曲面的情况呢？正如你所看到的，随机地往曲面上扔一个弹珠，少数情况下弹珠能够滚到曲面的全局最低处。换句话说，就是在多数情况下，石头都只能滚到曲面的局部最低处。这种情况下，你该怎么处理？你会试图着朝某个方向把石头推到曲面上的另一个点吗？显然，这种情况比凸曲面的情况更加复杂。

弹珠的比喻很有意思，因为它跟一个叫做梯度下降的最优化算法的思想基本上是一样的。另一个求解最优化问题的方法就是使用众所周知的牛顿法。我鼓励感兴趣的读者去深入研究一下这些算法并且试着自己写代码实现它们。

4.总结

在这一部分，学习了凸集的概念和如何判定一个函数是否为凸函数。此外，最后我们举了弹珠的例子来简单明了的说明了为什么凸优化问题比非凸优化问题更加简单：因为凸优化问题中的局部极小值就是全局最小值。