JAVA实现双边决策
Posted xiaojimanman
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了JAVA实现双边决策相关的知识，希望对你有一定的参考价值。
转载请注明出处：http://blog.csdn.net/xiaojimanman/article/details/50373369
http://www.llwjy.com/blogdetail/782eade38b1a3a644ac8296f1f438135.html
个人博客站已经上线了，网址 www.llwjy.com ~欢迎各位吐槽~
-------------------------------------------------------------------------------------------------
现实生活中存在很多问题，比如商品买卖如何实现商家利润最大化？大学生招生录取如何实现整体效果最好？病人医生如何实现整体服务水平最高等？这些我们都可以把他统一的转化为双边决策问题。下面先说说自己对双边决策的理解。
双边决策——个人理解
为了帮助大家理解，我用一个简单的例子介绍什么是双边决策，加入现在市场上有10位顾客，分别为A0、A1、A2、A3、A4、A5、A6、A7、A8、A9，市场上有是个商品，分别为B0、B1、B2、B3、B4、B5、B6、B7、B8、B9，现在要求要把这10个商品分别分给这10位顾客，要求整体的满意程度最高，当然每位顾客对每个商品的打分是不一样的，加入M位顾客对N件商品的满意度为AMBN，那么如何分配这些商品才能使整体的满意度最高？像这个为题就是一个双边决策问题。
算法介绍
目前关于双边决策的实现算法有很多，下面就介绍一种自己想到的（如有雷同，纯属巧合），这个算法是基于之前自己写的一篇遗传算法的文章想到的。自己这个算法要求顾客和商品的数目必须一致，并且是一对一的关系，如果数目不一致或者是一对N（N是一个具体值）的时候，我们可以通过构建虚拟的商品（顾客）来使用这个算法，下面我就简单介绍下算法思想：
1）我们首先选取一个分配方案，这里我们不防假定初始的分配方案就是M件商品分给M位顾客；
2）我们将比较步长step设置为1；
3）判断step是否超过数组长度，如果超过结束算法，如果没超过继续执行下一步；
4）比较step步长下的两位顾客，假设将他们的分配方案对调，如果对调之后的满意度大于对调前的满意度就进行对调，否则保持原样，将比较位往后移动一位继续进行第4）步；
5）该步长step下已经没有可以对调的分配方案，将步长step加1；
6）跳到第3）步继续执行。
在上述算法描述中，我们重点介绍下第4）步，这里我们假设第1位顾客分配的商品是1号商品，第2位顾客分配的商品是2号商品，他们对商品的满意度分别为A1B1、A2B2，这时这两个顾客的总体满意度为SCORE1=A1B1+A2B2，这里我们将他们的分配方案对调，也就是第1位顾客分配的商品是2号商品，第2位顾客分配的商品是1号商品，这时候他们对商品的满意度分别为A1B2、A2B1，这两个顾客的整体满意度为SCORE2=A1B2+A2B1，如果SCORE1小于SCORE2，那么我们就改变分配策略，否则保持原来的分配策略。
JAVA代码分析
对于上面的介绍也许并不是太具体，或者并不知道用JAVA如何实现，下面我们就对如何实现做拆解：
1）在写算法的时候，我们首先需要定义一些常量、保存分配方案等：
public class TwoSidedDecision
private int num = 10;//个体数目
private boolean maxFlag = true;//是否求最大值
private int[][] scoreArray;//AB之间的互评得分
private int[] decisionArray;//A选择B的方式
这里有一个maxFlag属性，他的作用是用来标识我们的双边决策是要取最大值还是要取最小值，true表示最大值，false表示最小值；num用来标识个体的个数，scoreArray数组用来表示用户对商品的满意度，decisionArray用来保存商品的分配方案，decisionArray[0]表示编号为0的顾客分配的商品是decisionArray[0]；
2）在运行算法之前，我们需要设置个体数目
public void setNum(int num)
if (num < 1)
System.out.println("num must be greater than 0");
return;
this.num = num;
3）顾客对商品进行 满意度打分并确定初始分配方案
public void setScoreArray(int[][] scoreArray)
if (scoreArray == null)
System.out.println("scoreArray is null");
if (!(scoreArray.length == num && scoreArray[0].length == num))
System.out.println("scoreArray`s must be " + num);
this.scoreArray = scoreArray;
decisionArray = new int[num];
//初始决策，对角线
for (int i = 0; i < num; i++)
decisionArray[i] = i;
decision();
4）然后进行算法描述中的第4）步，确认 分配方案是否对调
private boolean compare(int stepSize)
for (int i = 0; i < num - stepSize; i++)
int a1 = i;
int a2 = i + stepSize;
int b1 = decisionArray[a1];
int b2 = decisionArray[a2];
//原始两个得分之和
int score1 = scoreArray[a1][b1] + scoreArray[a2][b2];
int between1 = Math.abs(scoreArray[a1][b1] - scoreArray[a2][b2]);
//交换后的两个得分之和
int score2 = scoreArray[a1][b2] + scoreArray[a2][b1];
int between2 = Math.abs(scoreArray[a1][b2] - scoreArray[a2][b1]);
if (maxFlag) //最后的得分最大
if (score1 <= score2) //交换后的分数不小于交换前的
//交换后的分数大于交换前的或者交换后的差值大于交换前的
if (score1 < score2 || between2 > between1)
decisionArray[a1] = b2;
decisionArray[a2] = b1;
return true;
else //最后的得分最小
if (score1 >= score2) //交换后的分数不小于交换前的
//交换后的分数大于交换前的或者交换后的差值大于交换前的
if (score1 > score2 || between2 > between1)
decisionArray[a1] = b2;
decisionArray[a2] = b1;
return true;
return false;
运行结果
最大值测试
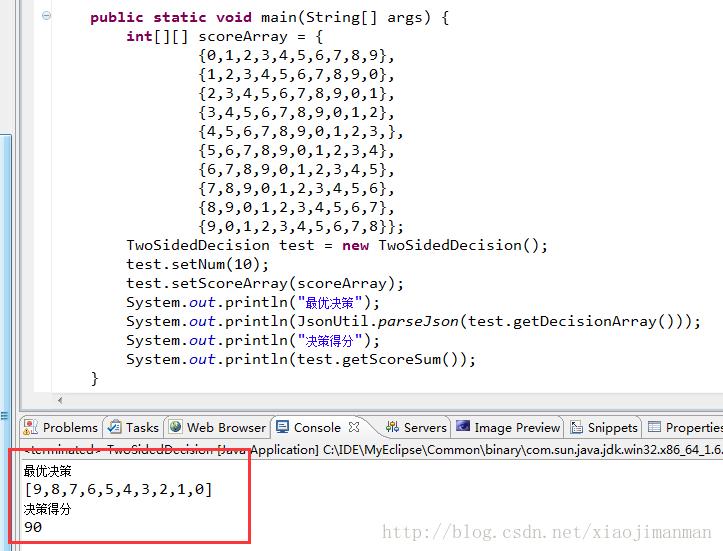
最小值测试
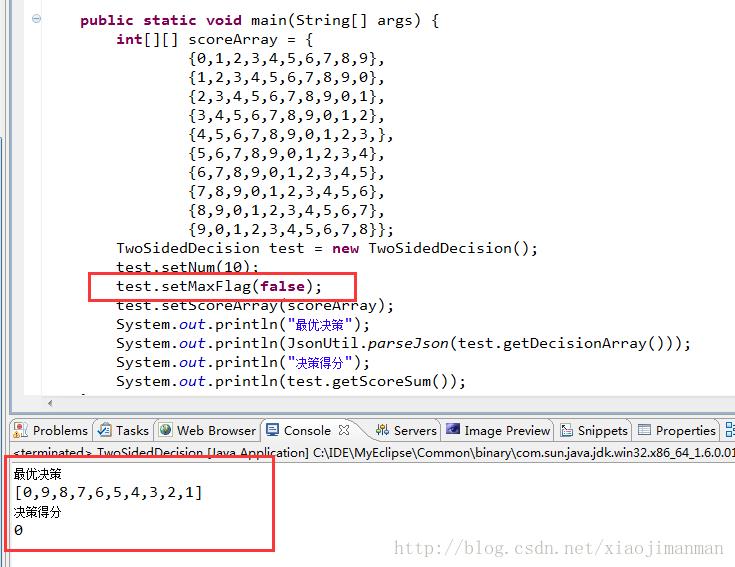
完整代码
/**
*@Description: 双边匹配决策算法
*/
package com.lulei.twosided.matching.decisionmaking;
import com.lulei.util.JsonUtil;
public class TwoSidedDecision
private int num = 10;//个体数目
private boolean maxFlag = true;//是否求最大值
private int[][] scoreArray;//AB之间的互评得分
private int[] decisionArray;//A选择B的方式
public boolean isMaxFlag()
return maxFlag;
public void setMaxFlag(boolean maxFlag)
this.maxFlag = maxFlag;
/**
* @return
* @Author:lulei
* @Description: 获得最后的决策
*/
public int[] getDecisionArray()
return decisionArray;
/**
* @return
* @Author:lulei
* @Description: 获取决策的评分
*/
public int getScoreSum()
int sum = 0;
for (int i = 0; i < num; i++)
sum += scoreArray[i][decisionArray[i]];
return sum;
/**
* @param num
* @Author:lulei
* @Description: 设置双边决策个体个数
*/
public void setNum(int num)
if (num < 1)
System.out.println("num must be greater than 0");
return;
this.num = num;
/**
* @param scoreArray
* @Author:lulei
* @Description: 设置A类个体与B类个体间的评价
*/
public void setScoreArray(int[][] scoreArray)
if (scoreArray == null)
System.out.println("scoreArray is null");
if (!(scoreArray.length == num && scoreArray[0].length == num))
System.out.println("scoreArray`s must be " + num);
this.scoreArray = scoreArray;
decisionArray = new int[num];
//初始决策，对角线
for (int i = 0; i < num; i++)
decisionArray[i] = i;
decision();
/**
* @Author:lulei
* @Description: 计算最优决策
*/
private void decision()
if (scoreArray == null || decisionArray == null)
System.out.println("please init scoreArray");
for (int stepSize = 1; stepSize < num; stepSize++)
//特定步长下的交换
while (compare(stepSize));
/**
* @param stepSize
* @return
* @Author:lulei
* @Description: 特定步长比较，返回值确认是否发生交换
*/
private boolean compare(int stepSize)
for (int i = 0; i < num - stepSize; i++)
int a1 = i;
int a2 = i + stepSize;
int b1 = decisionArray[a1];
int b2 = decisionArray[a2];
//原始两个得分之和
int score1 = scoreArray[a1][b1] + scoreArray[a2][b2];
int between1 = Math.abs(scoreArray[a1][b1] - scoreArray[a2][b2]);
//交换后的两个得分之和
int score2 = scoreArray[a1][b2] + scoreArray[a2][b1];
int between2 = Math.abs(scoreArray[a1][b2] - scoreArray[a2][b1]);
if (maxFlag) //最后的得分最大
if (score1 <= score2) //交换后的分数不小于交换前的
//交换后的分数大于交换前的或者交换后的差值大于交换前的
if (score1 < score2 || between2 > between1)
decisionArray[a1] = b2;
decisionArray[a2] = b1;
return true;
else //最后的得分最小
if (score1 >= score2) //交换后的分数不小于交换前的
//交换后的分数大于交换前的或者交换后的差值大于交换前的
if (score1 > score2 || between2 > between1)
decisionArray[a1] = b2;
decisionArray[a2] = b1;
return true;
return false;
public static void main(String[] args)
int[][] scoreArray =
0,1,2,3,4,5,6,7,8,9,
1,2,3,4,5,6,7,8,9,0,
2,3,4,5,6,7,8,9,0,1,
3,4,5,6,7,8,9,0,1,2,
4,5,6,7,8,9,0,1,2,3,,
5,6,7,8,9,0,1,2,3,4,
6,7,8,9,0,1,2,3,4,5,
7,8,9,0,1,2,3,4,5,6,
8,9,0,1,2,3,4,5,6,7,
9,0,1,2,3,4,5,6,7,8;
TwoSidedDecision test = new TwoSidedDecision();
test.setNum(10);
test.setMaxFlag(false);
test.setScoreArray(scoreArray);
System.out.println("最优决策");
System.out.println(JsonUtil.parseJson(test.getDecisionArray()));
System.out.println("决策得分");
System.out.println(test.getScoreSum());
-------------------------------------------------------------------------------------------------
小福利
-------------------------------------------------------------------------------------------------
个人在极客学院上《Lucene案例开发》课程已经上线了（目前上线到第二课），欢迎大家吐槽~ 第七课：小说网站分布式爬虫的实现
以上是关于JAVA实现双边决策的主要内容，如果未能解决你的问题，请参考以下文章
R语言plotly可视化：使用plotly可视化多分类模型的预测置信度模型在2D网格中每个数据点预测的置信度置信度定义为在某一点上最高分与其他类别得分之和之间的差值
R语言决策树bagging随机森林模型在训练集以及测试集的预测结果（accurayF1偏差Deviance）对比分析计算训练集和测试集的预测结果的差值来分析模型的过拟合（overfit）情况