支配树学习思路/模板

Posted 2022-12-12 Kalzn

首先解释什么是支配树。
首先我们先看一下DAG，我们现在有一个DAG：

如果我们从1出发，对于图中的一个点$p$,在从1到$p$的不同路径中，总有一些点是必经的，例如图中的8号点，我们发现在从1到8的不管是那一条路径上，5都是必须经过的。（当然1号点和8号点也可以理解为必经的）。对于每一个点，如果把该点向上最近的一个必经点和该点连有向边。我们就得到了这个图的支配树。
还是那这个DAG举例，我们按照上述的方法连边（红线）：

红边就是该DAG的支配树。对于一个点$p$，从其到1的树链上的每一个点，都是1到$p$的必经点。
我们仔细观察这个图，我们发现，对于一个点，他最近的必经点（支配树父亲）都是他的所有入点的“LCA”。例如，5号点的入点V= 6,2,3 ,其”LCA”为1。同理8号点，入点的“LCA”为5。那么我们怎么求这个所谓的“LCA”呢？
我们都知道，“LCA”的概念仅存在于树上，对于DAG，对于一个点集没有所谓固定的“LCA”（因为一个点可能不止一个父亲（入点））。但是对于上图，我们可以考虑，如果一个点的所有入点向上的支配树已经建成，那么该点的最近必经点就是这些入点在当前已建支配树上的LCA
有点绕。。。我们看例子，比如现在我们要确定5号点的最近必经点。且V= 6,2,3 向上的支配树已经建成。那么此时图是这样的：

从图上非常明显的知道：V= 6,2,3 的在已建成的支配树上的LCA为1。这时我们连边<1, 5>

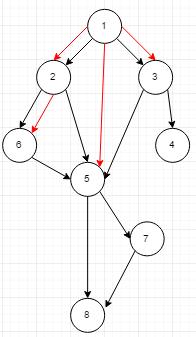
对于其他的点，同理。所有我们知道，我们在依次建立支配树的边时，必须保证该点的所有入点的支配树都已建成。所以，我们必须先处理每个点的入点，在处理该点。。这不就是 拓扑排序么？我们可以按照拓扑顺序处理完这个DAG，建成支配树。下面看一个例题。
P2597 [ZJOI2012]灾难
相信这个题，已经在各种大佬博客、题解中看了不止一遍了。我们如果用上述方法建成该食物网的支配树。那么每个点的答案，就该点的支配树子树的大小了。
我们看代码：首先建图：

void add(int x, int y)

    ver[++tot] = y;
    ne[tot] = he[x];
    he[x] = tot;
    verf[tot] = x;
    nef[tot] = hef[y];
    hef[y] = tot;

scanf("%d", &n);
for (int i = 1; i <= n; i++)

	int x;
	while(scanf("%d", &x), x)
	di[i]++;add(x, i);

可以看到，在建图的时候，我们统计入度，并同时建出反图（一会提到为什么）
然后我们拓扑排序，得到点的拓扑序：

void topu()

    for (int i = 1; i <= n; i++) if (!di[i])
        q.push(i);
    while(q.size())
    
        int now = q.front();
        q.pop();
        topp[++cnt] = now;//记录拓扑序
        for (int i = he[now]; i; i = ne[i])
        
            int y = ver[i];
            di[y]--;
            if (!di[y])
                q.push(y);
        
    

然后我们我们按照拓扑顺序建立支配树:

void adda(int x, int y)

    vera[++tot] = y;
    nea[tot] = hea[x];
    hea[x] = tot;

for (int i = 1; i <= n; i++)

    int x = verf[hef[topp[i]]];//利用反图，找到topp[i]点的入点
    for (int j = hef[topp[i]]; j; j = nef[j])
        x = lca(x, verf[j]);//遍历所有入点，算出lca
    adda(x, topp[i]);//联边建树
    d[topp[i]] = d[x] + 1;
    f[topp[i]][0] = x;
    for (int j = 1; j <= 25; j++)
        f[topp[i]][j] = f[f[topp[i]][j-1]][j-1];//边建树便记录f数组

此时hea系列数组记录的就是支配树信息。
最后我们dfs一下支配树，记录子树大小就可以了。
下面是完整ac代码：

#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string>
#include <vector>
#include <map>
#include <cstdlib>
#define ll long long
using namespace std;
const int N = 2e5+5;
int tot, he[N], ver[N], ne[N];
int hef[N], verf[N], nef[N];
int tota, hea[N], vera[N], nea[N];
int f[N][30], d[N];
int di[N];
int n,m, cnt, topp[N];
queue<int> q;
void add(int x, int y)

    ver[++tot] = y;
    ne[tot] = he[x];
    he[x] = tot;
    verf[tot] = x;
    nef[tot] = hef[y];
    hef[y] = tot;

void adda(int x, int y)

    vera[++tot] = y;
    nea[tot] = hea[x];
    hea[x] = tot;

void topu()

    for (int i = 1; i <= n; i++) if (!di[i])
        q.push(i);
    while(q.size())
    
        int now = q.front();
        q.pop();
        topp[++cnt] = now;
        for (int i = he[now]; i; i = ne[i])
        
            int y = ver[i];
            di[y]--;
            if (!di[y])
                q.push(y);
        
    

int lca(int x, int y)

    if (d[x] > d[y]) swap(x, y);
    for (int i = 25; i >= 0; i--)
    
        if (d[f[y][i]] < d[x]) continue;
        y = f[y][i];
    
    if (x == y) return x;
    for (int i = 25; i >= 0; i--)
        if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
    return f[x][0];

int siz[N];
int dfs(int now)

    siz[now] = 1;
    for (int i = hea[now]; i; i = nea[i])
    
        siz[now] += dfs(vera[i]);
    
    return siz[now];

int main()

    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    
        int x;
        while(scanf("%d", &x), x)
        di[i]++;add(x, i);
    
    topu();
    for (int i = 1; i <= n; i++)
    
        int x = verf[hef[topp[i]]];
        for (int j = hef[topp[i]]; j; j = nef[j])
            x = lca(x, verf[j]);
        adda(x, topp[i]);
        d[topp[i]] = d[x] + 1;
        f[topp[i]][0] = x;
        for (int j = 1; j <= 25; j++)
            f[topp[i]][j] = f[f[topp[i]][j-1]][j-1];
    
    dfs(0);
    for (int i = 1; i <= n; i++)
        printf("%d\\n", siz[i]-1);
    return 0;

很好，我们现在探讨完DAG的情况了，终于进入最普遍的支配树的学习了。即：一般有向图的支配树与支配点（即必经点）。
下面有一个有向图：
（蓝色边为其dfs搜索树的边，为方便每个点的编号都是它的dfn）

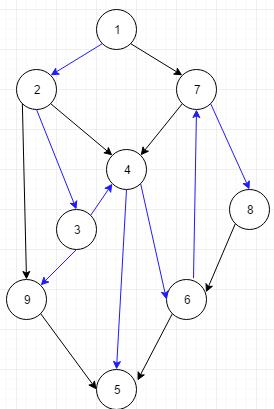
这里我引入半支配点的概念：对于图，若存在一个简单路径<x,y>。如果从x到y所经历的所有点（除了x，y）的时间戳都大于y的时间戳，我们认为x为y的半支配点
例如图中的6号点，他的半支配点集为V = 4，7，8，1。因为从这些点出发都可以找到一个简单路径到达6，且满足上述条件（如图红边所示）：

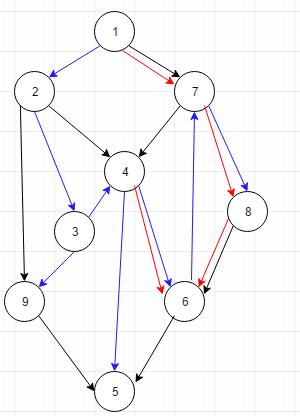
对于每一个点，我们找到他的半支配点集中的dfn最小的一个，记做$semi[x]$
然后对于每一个<$semi[x]$, $x$>连边。（如图红边所示）

为什么要这么做？因为我们如果把所有非搜索树的边删去，链接<$semi[x]$, $x$>，那么对于每个点，其支配性不变。而又因为，对于每个点$x$，$semi[x]$都是它搜索树上的祖先。
对于一个点$x$找出所有的边$(y,x)$中对应的$y$
若$dfn[y]<dfn[x]$ 且$dfn[y]$比当前找到的$semi[x]$的$dfn$小 那么就用$semi[x]=y$
若$dfn[y]>dfn[x]$找打树上$y$的一个祖先$z$ 并且$dfn[z]>dfn[x]$比较$semi[z]$同$semi[x]$决定是否用前者更新后者。
这时，我们发现图变成了下面的样子：

没错，它变成了一个DAG。结合上述定理（支配性不变）。我直接按照DAG的支配树求法去求这个图的支配树。除此之外，但是我们有更好的办法。
对于一个点的最近支配点，我们记为$idom[x]$，我们知道，如果求出这个玩意，然后对于每个点建边<$idom[x],x$>就是支配树了。。那么我们怎么求$idom[x]$呢？
（摘自洛谷）
我们令$P$是从$semi[x]$到$x$的搜索树上路径点集(不包括$semi[x]$) 而且 z