卡特兰数——小兔的棋盘 （HDU 2067）

Posted 2022-12-12 mid2dog

前言

在这里存档以免以后再遇见卡特兰数一概不知。。。。

---

开工

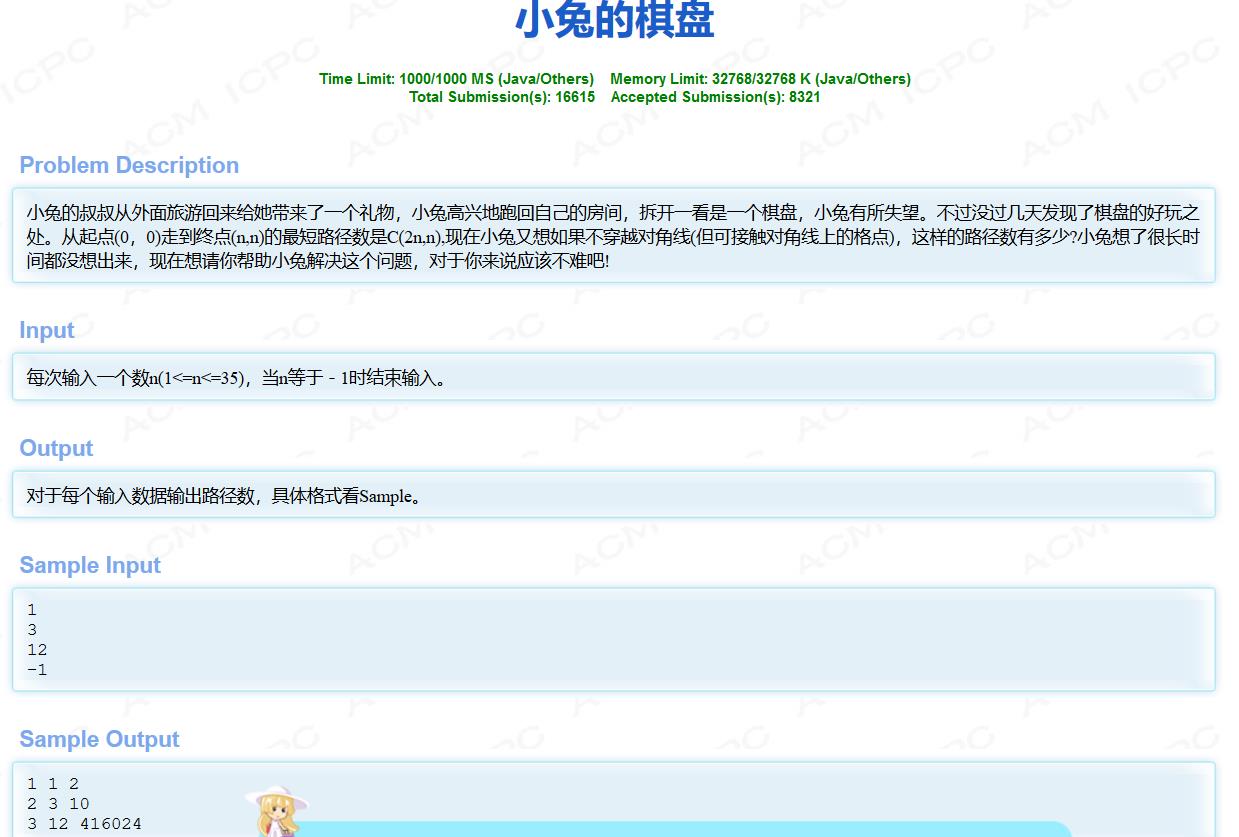嗯，懵，很懵。

然后据度娘所说是个卡姿兰数，呃，不好意思，卡特兰数。

看了半天卡特兰数也不知道这是个什么魔鬼东西，看得来的方式更令人头大，干脆直接记住推导公式与相应需要用到的情况好啦，毕竟懒癌晚期了

开工！

https://blog.csdn.net/jokerwyt/article/details/77414853
这里面是需要用到卡特兰数的相应情况

记住开头几项以及实际意义中需要用到的应该就好了，嗯哼

这道题就是卡特兰数的一个简单应用，如下图
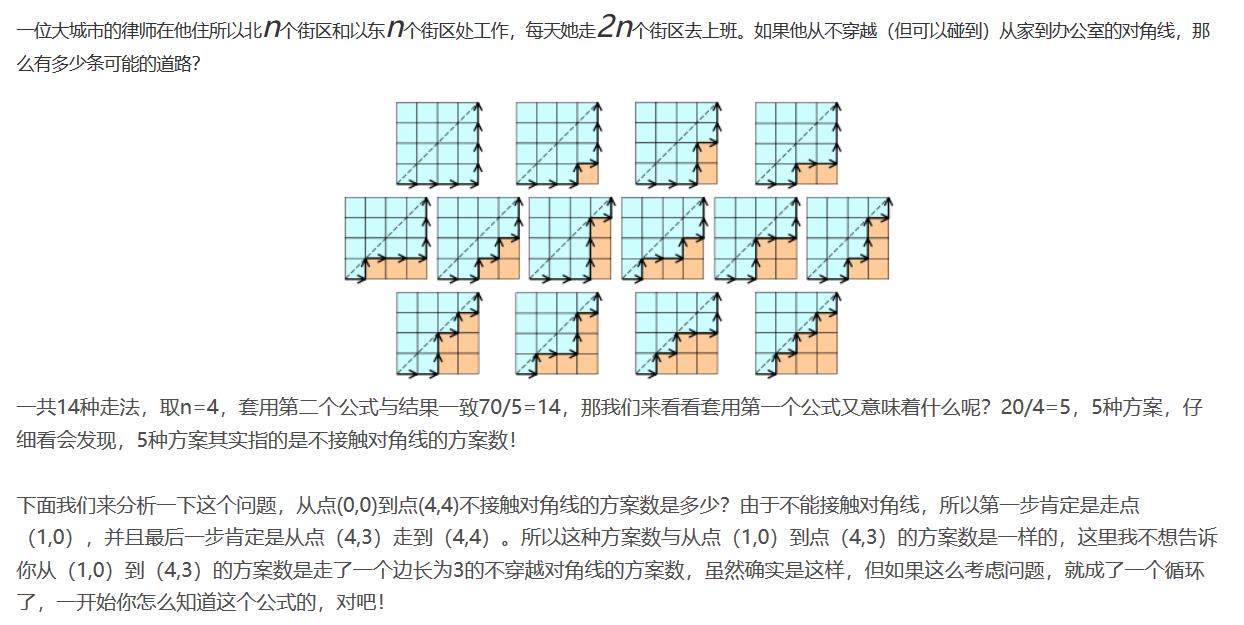顺便放上url

而且套公式也不能随便套。。。因为

有两个公式

一个是

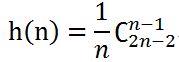
这个刚好是不经过对角线的结果

另一个

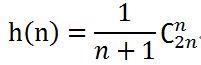
这个刚好是经过对角线的结果

于是乎，自然而然地选择了第二个，接下来就是快乐的ac时间咯。

等等，还有个问题，C(n,2n)组合数 如何用算法来表达

题目要求达到了35，而35！估计达到了相当恐怖的数字。。。

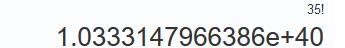
果断抛弃直接算，选择用递归来算出组合数

递归的话高中学过的

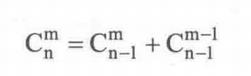
这个公式应该是高中熟知的哈哈

那么递归结束条件就是m为0的时候或者m与n相等的时候出1

你问我为什么m和n相等也出1？ C（n,n)不是等于1么。。

于是乎

long long pet(int m,int n)
if ( m==0 || n==m )return 1;
return	pet(m,n-1)+pet(m-1,n-1); 

然后想到杭电oj总是有多组数据，那样就要重复计算好多次，麻烦，于是改成数组，这样就不用重复算了

long long a[100][100]=0;
long long pet(int m,int n)
if ( m==0 || n==m )return 1;
 if (a[m][n]!=0) return a[m][n]; //这样已经计算过就不会向下递归而是直接返回
return	a[m][n]=pet(m,n-1)+pet(m-1,n-1); 

简单明了，开心顺畅
这个就诠释了为什么答案会比卡特兰数大两倍哈哈

代码

#include<stdio.h>
long long a[40][40]=0;
long long pet(int m,int n)

	if(m==0||n==m)return 1;
	if(a[m][n]!=0)return a[m][n];
	return a[m][n]=pet(m,n-1)+pet(m-1,n-1);

int main()
	int num=0,n;
	while(~scanf("%d",&n)&&n!=-1)
		long long x=pet(n,2*n)/(n+1);
		printf("%d %d %lld\\n",++num,n,x*2);
	
 

然后你就会发现审判器说你这是错误答案，到34的时候变成了负数。

重新上百度
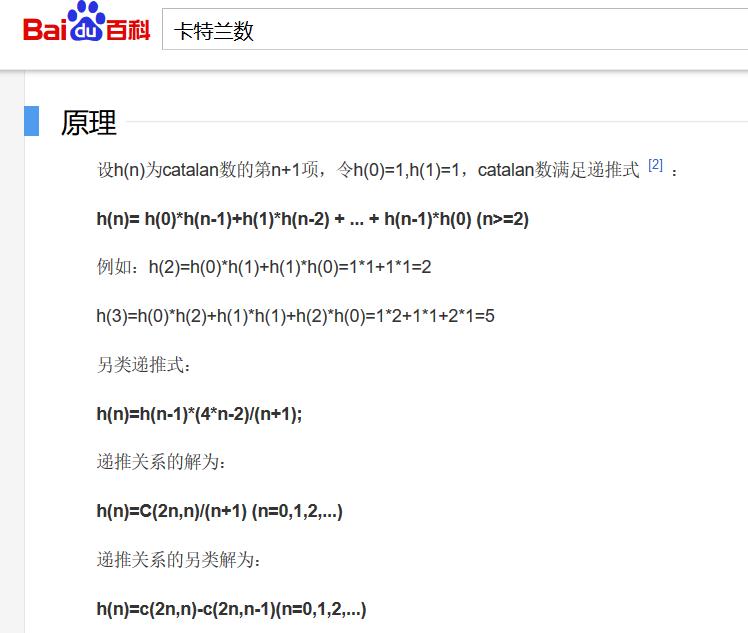发现度娘居然给你了看起来更简单的递推公式，我真的是&￥……%&……%&

然后来个循环叠加就好了

for(int i = 2 ; i <= 35 ; i++)
	for(int j = 0; j<= i-1; j++)
		h[i]+=h[j]*h[i-j-1];

哎
最后ac代码如下

#include<stdio.h>
int main()

	long long h[40]=1,1;
	for(int i = 2 ; i <= 35 ; i++)
		for(int j = 0; j<= i-1; j++)
			h[i]+=h[j]*h[i-j-1];
	int n,num=1; 
	while(scanf("%d",&n)&&n!=-1)
		
		printf("%d %d %lld\\n",num++,n,h[n]*2);