带你辨析最小生成树的两种算法

Posted 2022-12-12 杨东冀@pku

最小生成树的算法通常由在几个城市中间修筑路径使其连通并且花费最小引出。如下图所示引例。

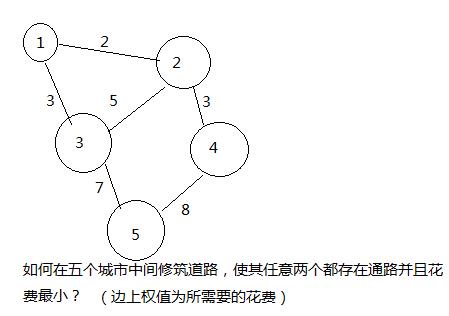
多数求最小生成树算法都应用了简称为MST的性质：假设N=（V，E）是一个连通网，U是顶点V的一个非空子集。若（u，v）是一条具有最小权值的边，其中u∈U,v∈V-U,则必存在一个包含(u,v)的最小生成树。

下面介绍普里姆算法：

prime算法的基本思想

1.构造一个空树，任取一个顶点加入生成树

2.在那些一个端点在生成树里，另一个端点不在生成树里的边中，选取一条权最小的边，将它和另一个端点加进生成树

3.重复步骤2，直到所有的顶点都进入了生成树为止，此时的生成树就是最小生成树

int prime(int cur)

    int index;
    int sum = 0;
    memset(visit, false, sizeof(visit));
    visit[cur] = true;
    for(int i = 0; i < m; i ++)
        dist[i] = graph[cur][i];    
    

    for(int i = 1; i < m; i ++)

        int mincost = INF;
        for(int j = 0; j < m; j ++)
            if(!visit[j] && dist[j] < mincost)
                mincost = dist[j];
                index = j;    
                
        

        visit[index] = true;
        sum += mincost;

        for(int j = 0; j < m; j ++)
            if(!visit[j] && dist[j] > graph[index][j])
                dist[j] = graph[index][j];
                
            
     
    return sum;    
 

克鲁斯卡尔算法：
令最小生成树的初始状态为只有n个顶点而不具有边的非连通图T=（V，），使其每个顶点自成一个连通分量，在E边集中依次选择代价自小的边，如果边依附的顶点落在T中不同的连通分量上，则将其加入到T中，否则舍弃此边选择下一条代价最小的边。

#include<iostream>
#include<algorithm>
using namespace std;

const int size = 128; 
int n;
int father[size];
int rank[size];

//把每条边成为一个结构体，包括起点、终点和权值 
typedef struct node

    int val;
    int start;
    int end;    
edge[SIZE * SIZE / 2];

//把每个元素初始化为一个集合 
void make_set()

    for(int i = 0; i < n; i ++)
        father[i] = i;
        rank[i] = 1;    
        
    return ;


//查找一个元素所在的集合,即找到祖先 
int find_set(int x)

    if(x != father[x])
        father[x] = find_set(father[x]);    
        
    return father[x];


//合并x,y所在的两个集合：利用Find_Set找到其中两个
//集合的祖先，将一个集合的祖先指向另一个集合的祖先。
void Union(int x, int y)

    x = find_set(x);    
    y = find_set(y);
    if(x == y)
        return ;    
    
    if(rank[x] < rank[y])
        father[x] = find_set(y);    
    
    else
        if(rank[x] == rank[y])
            rank[x] ++;    
            
        father[y] = find_set(x);
    
    return ;


bool cmp(pnode a, pnode b)

    return a.val < b.val;    


int kruskal(int n) //n为边的数量 

    int sum = 0;
    make_set();
    for(int i = 0; i < n; i ++)   //从权最小的边开始加进图中 
        if(find_set(edge[i].start) != find_set(edge[i].end))
            Union(edge[i].start, edge[i].end);
            sum += edge[i].val;    
            
    
    return sum;    


int main()

    while(1)
        scanf("%d", &n);    
        if(n == 0)
            break;    
        
        char x, y;
        int m, weight;
        int cnt = 0;
        for(int i = 0; i < n - 1; i ++)
            cin >> x >> m; 
            //scanf("%c %d", &x, &m);    
            //printf("%c %d ", x, m);
            for(int j = 0; j < m; j ++)
                cin >> y >> weight; 
                //scanf("%c %d", &y, &weight);
                //printf("%c %d ", y, weight);    
                edge[cnt].start = x - 'A';
                edge[cnt].end = y - 'A';
                edge[cnt].val = weight;
                cnt ++;
            
        

        sort(edge, edge + cnt, cmp); //对边按权从小到大排序 
        cout << kruskal(cnt) << endl; 
        

初看两种算法看似是一样的都在选择最小边加入集合，普里姆算法是从已加入集合的点向未加入集合的点连代价最小的边（即不断地选择点），直到构成最小生成树。而克鲁斯卡尔算法是在任意两点间选择最小的代价（即选择边）只要其不形成环。