Unity3D 四元数的常用方法

Posted 2022-12-11 暗光之痕

环境：Unity2018.3 语言：C#

 

总起：

本文主要参考《3D数学基础：图形与游戏开发》。

 

四元数：

负四元数：

q=-q，同一个四元数有两个表示方式，他们互相为负。（下文只举四元数的一种形式）

 

单位四元数：

[1, 0]，即cos(θ/2)=1，θ为4πk，则sinθ=0，不管轴是什么，不进行旋转就是本身。

 

对应Unity中的Quaternion.identity。

 

四元数的模：

|q|=sqrt(w^2 + x^2 + y^2 + z^2)=sqrt(cos(θ/2)^2+sin(θ/2)^2 |n|^2)。关于旋转，我们只讨论单位四元数。

 

对应Unity中的Quaternion.Normalize。

 

四元数的共轭：

q*=[w, n]*=[w, -n]，四元数的逆q-1=q* / |q|，因此单位四元数下，共轭和逆是相同的。

 

对应Unity中的Quaternion. Inverse。

 

四元数的叉乘：

[w1, n1]*[w2, n2] = [w1w2-n1·n2  w1n2+w2n1+n2*n1]

 

叉乘代表的是旋转的累加。

 

假设有一个标准点p(x, y, z)=[0, (x, y, z)]，绕着n旋转θ，即q=[cos(θ/2), sin(θ/2)n]，可以得到p’=qpq-1。

 

但是这里带来一个问题，假设p’=b(apa-1)b-1 = (ba)p(ba)-1，这边的ba因为向量部分叉乘后的结果是相反的，导致内部向量变成ab的形式了，这样就不能继续对p进行变换了，因为顺序发生了改变。

 

为了解决以上问题，我们把标准公式改为下面的形式：

[w1, n1]*[w2, n2] = [w1w2-n1·n2  w1n2+w2n1+n1*n2]

 

则p’的结果也会发生变化：

p’=q-1pq

 

我们可以看到Unity中的实现就是如此：

 

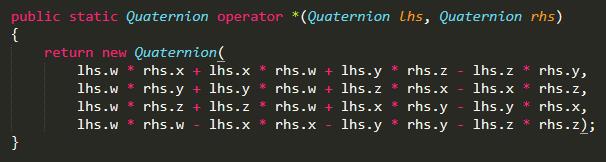
对应Unity中的方法是Quaternion.operator*。

 

四元数的差：

角位移d=a-1b，a和b是两个方位，以上公式根据两个方位算出需要经过的角位移。

 

对应Unity中的方法是Quaternion. FromToRotation。

 

四元数的点乘：

q1·q2=w1w2+x1x2+y1y2+z1z2

 

跟两个向量做点乘效果一模一样，所代表的是两个四元数的相似性。结果是1，则两个四元数相同；结果是0，则如果一个四元数一个轴旋转90度，另一个四元数旋转270度。（得出的结果可能是-1，但是跟1的结论是一样的，所以一般得到结果之后我们会取绝对值）

 

对应Unity中的方法是Quaternion. Dot；还有判断两个四元数是否使用了该方法：

 

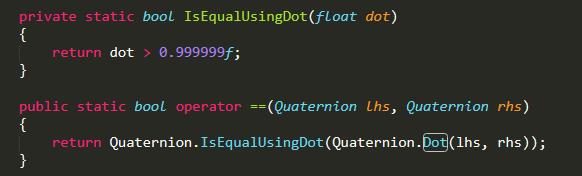
四元数的构造方法：

Quaternion.Euler(Vector3)  以欧拉角创建四元数

 

Quaternion.AxisAngle(Vector3,float)  相对于某个方向旋转某个角度的四元数

 

Quaternion.FromToRotation(Vector3,Vector3)  起始方向到结束方向的四元数

 

Quaternion.LookRotation(Vector3)  朝向为正方向，旋转轴为上方向，旋转到想要方向的四元数

 

没有讲到的部分：

四元数的对数、指数和标量乘在游戏中较少使用，这边不花精力去研究了。

 

还有个非常重要的方法：插值。关于这部分，我想单独起一篇文章来说明。