编辑距离（动态规划）

Posted 2022-12-10 北川_

题目描述
给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

编辑距离：是指两个字符串之间，由一个转成另一个所需的最少编辑操作次数。
问题：word1到word2的编辑距离
子问题：word1前i个字符到word2前j个字符的编辑距离
假如有两个字符串"hat"和"wtct"
每个格子表示word1前i个字符到word2前j个字符的编辑距离

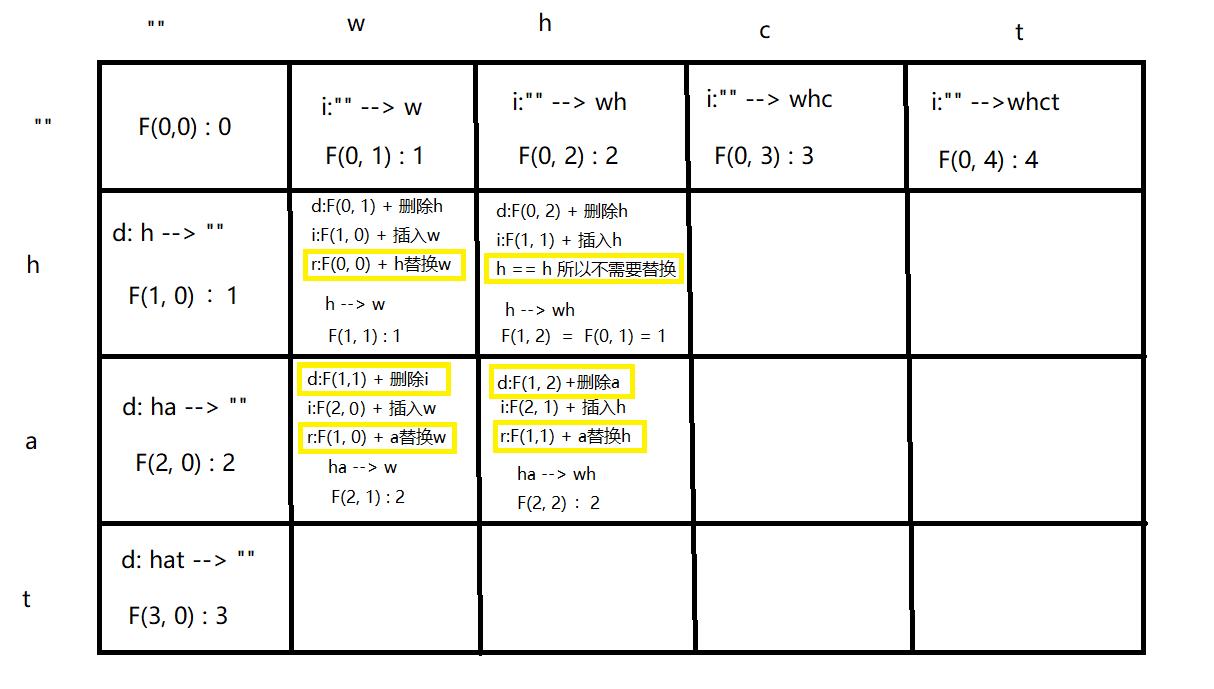
i表示插入操作，d表示删除操作，r表示替换操作。

第一行w可以由空字符串“”插入一个w得到，操作一次；wh可以由“”插入w再插入h得到，插入两次，依次得到“”到whct的操作次数。

第一列由h变为“”可以对h进行一次删除操作，由ha变为“”可以先删除h再删除a，操作两次；由hat变为“”可以进行三次删除操作依次删除三个字母。

F(1, 1)表示由h变为w的编辑距离，
由h到w，可以先在h前面插入一个w，变为wh，再把h删除，操作两次，即用F(0, 2)的状态下再加一次删除操作。
还可以先把h删除，再插入一个w，操作两次，即用F(1, 0)的状态再加一次插入操作。
还可以把h替换成w，操作一次，可以用F(0, 0)的状态加一次替换操作表示。
这三种操作都能将h变为w，而我们需要的是最少的操作次数，所以选择替换。F(1,1) 就为1。

F(1, 2)表示h变为wh的编辑距离，
由h到wh，可以先在h的前面进行两次插入操作插入wh，再将原来的h删除，即可以用F(0, 2)的状态加一次删除操作。
还可以把h先替换成w，然后再插入h，即F(1, 1)的状态再加一次插入操作。
还可以再h的前面直接插入w，即F(0, 1)的状态，由于字符h和wh的第二个字符相同，所以不需要再进行替换操作，用F(0, 1)的状态就可以表示F(1, 2)。
在这三种操作中，删除操作是2+1为3，插入操作为1+1为2，不需要替换用F(0, 1)表示为1,。所以F(1, 2)为1。

F(2, 1)表示ha变为w的编辑距离，
由ha变为w，可以先将h变为w，再把a删除，即用F(1, 1)的状态再加一次删除操作。
还可以将ha变为""，再插入w，即用F(2, 0)再加一次插入操作。
还可以将h删除，将a替换成w，即用F(1, 0)的状态加一次替换操作。
删除要两次，插入要三次，替换要两次。
所以F(2, 1)为2。

F(2, 2)表示ha变为wh的编辑距离，
由ha变为wh，可以先将h变为wh，再删除a，即用F(1, 2)的状态再加一次删除操作。
还可以ha先变为w，再插入h，即F(2, 1)的状态再加一次插入操作。
还可以将h替换成w，再将a替换成h，即F(1, 1)的状态再加一次替换操作。
在这一步想要进行删除操作需要2次(F(1, 2) + 1), 进行插入操作需要
3次(F(2, 1 + 1)), 进行替换操作需要2次(F(1, 1) + 1)，所以F(2, 2)为2。

经过分析可以得出状态转移方程：
word2的每一个子串都可由word1的子串进行插入，删除，替换这三种操作得到，我们需要的是操作次数最少的结果，即：
F(i, j) = min(插入，删除，替换)
F(i, j) = min(F(i, j - 1) + 1, F(i - 1, j) + 1, F(i - 1, j - 1) + (w1[i] == w2[j] ? 0 : 1))
这里需要注意的是替换操作如果word1[i]和word2[j]相等就不需要进行替换了。

代码：

class Solution 
public:
    int minDistance(string word1, string word2) 
        int row = word1.size() + 1;
        int col = word2.size() + 1;
        int dp[row][col];
        //把第一行和第一列初始化
        for(int j = 0; j < col; ++j)
        
            dp[0][j] = j;
        
        for(int i = 0; i < row; ++i)
        
            dp[i][0] = i;
        
        //依次算出上图每个格子的状态
        for(int i = 1; i < row; ++i)
        
            for(int j = 1; j < col; ++j)
            
            	//如果两次字符相等，不需要替换操作
            	//就像上图的由h-->wh
                if(word1[i - 1] == word2[j - 1])
                    dp[i][j] = dp[i - 1][j - 1];
                else
                    dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
            
        
        return dp[row - 1][col - 1];
    
;