二叉树前序，中序，后序遍历迭代实现详解

Posted 2022-12-10 加冰雪碧

二叉树的遍历迭代实现

在上一篇文章中实现了二叉树，但是对于遍历仅仅是简单的用递归来进行了实现。在这篇文章中将给出迭代的实现版本以及分析过程。

首先给出我们要分析的二叉树实例：

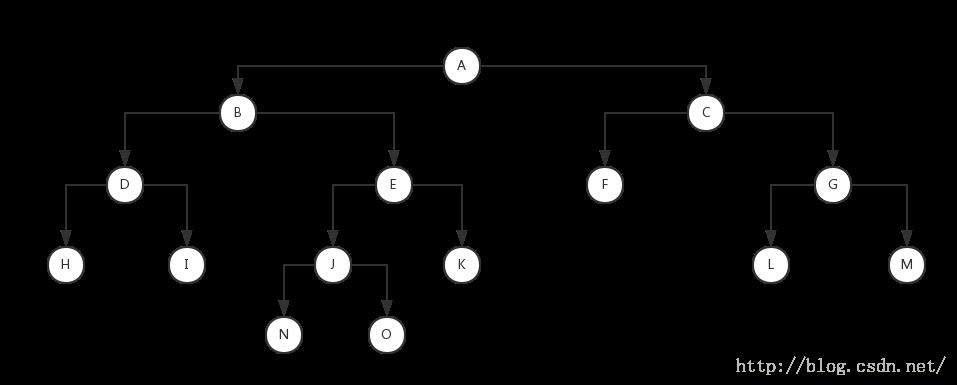
前序遍历迭代版本的分析及实现：

根据上面给出的二叉树进行前序遍历的分析，很容易得到正确的遍历顺序：

A B D H I E J N O K C F G L M

回顾我们手动得到前序遍历时的想法，我将遍历的过程分为几个步骤来阐述：

1.首先得到的是根节点，而后关注根节点的左子树，而后再关注左子树根节点的左子树......直到最终的某一个节点左子树不存在，在图中第一个左子树不存在的节点为H，不难发现，我们是一直沿着左子树下行的。

2.而后我们将进行回溯，找到最后一个遍历的，且右子树存在的节点。在图中，第一个这样的节点是D。

3.接下来对步骤2中所找到的节点进行步骤1的操作。

从上述的分析可以看出针对二叉树的前序遍历无非就是针对各个左子树根节点的遍历，如下图：

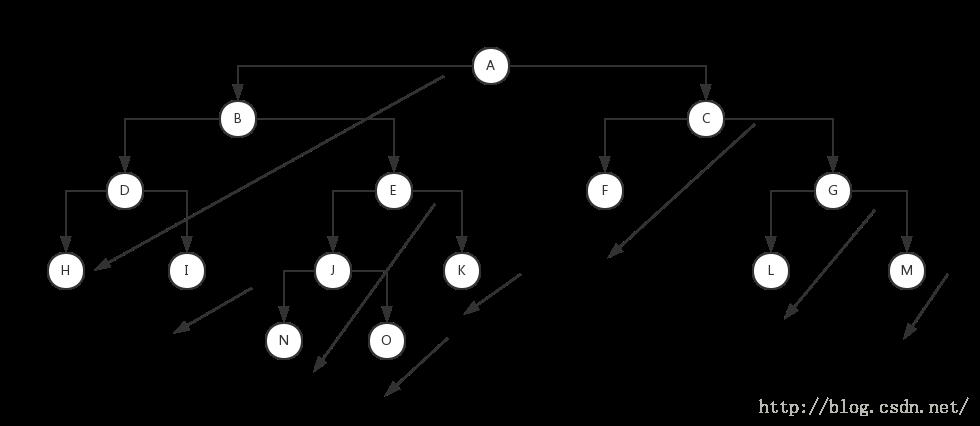
对以A为根的树进行A B D H的左侧遍历，对以I为根的子树进行I（因为子树中只有一个元素）的左侧遍历，其他节点同理。针对上述逻辑我们可以抽象出一个遍历规则，如下图所示：

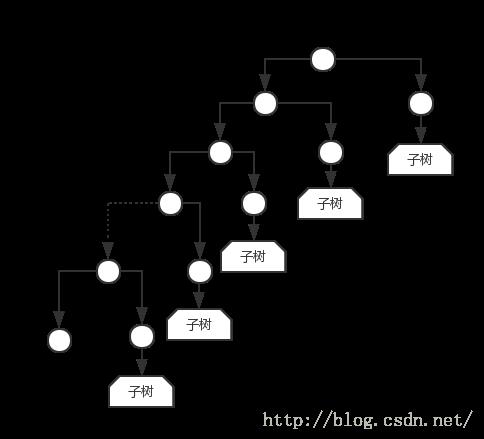
通过上图，能更好的说明上述左下行遍历的原理，我们可以发现，在一系列的子树中，后面的子树先来进行访问，是标准的LIFO，所以我们可以用栈来实现迭代的遍历。下面是具体的实现代码：

private void traversePartPreorder(BinaryNode<T> rootNode, Stack<BinaryNode<T>> stack)
		BinaryNode<T> currentNode = rootNode;
		while(currentNode != null)
			System.out.println(currentNode.getData());
			if(currentNode.getRightChild() != null)
				stack.push(currentNode.getRightChild());
			
			currentNode = currentNode.getLeftChild();
		
	

public void preorderTraverse() 
		
		Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
		BinaryNode<T> currentNode = root;
		while(true)
			traversePartPreorder(currentNode, stack);
			if(stack.isEmpty())
				break;
			
			currentNode = stack.pop();
		
	

其中所涉及的类是上文java二叉树的实现中编写的。

在第一个方法traversePart中我们一直沿左侧下行，将沿途出现节点简单输出，并且将其右节点都放入了栈中（只要它的右节点非空）。接下来的主方法中我们不断的从栈中取出节点，并把它作为根节点来重复traversePart中实现的步骤，最后当栈中不含有节点时方法返回。

下面是测试代码：

BinaryTreeInterface<String> hTree = new BinaryTree<String>();
		hTree.setTree("H");
		BinaryTreeInterface<String> iTree = new BinaryTree<String>();
		iTree.setTree("I");
		BinaryTreeInterface<String> dTree = new BinaryTree<String>();
		dTree.setTree("D",hTree,iTree);
		
		
		BinaryTreeInterface<String> nTree = new BinaryTree<String>();
		nTree.setTree("N");
		BinaryTreeInterface<String> oTree = new BinaryTree<String>();
		oTree.setTree("O");
		BinaryTreeInterface<String> jTree = new BinaryTree<String>();
		jTree.setTree("J",nTree,oTree);
		
		BinaryTreeInterface<String> kTree = new BinaryTree<String>();
		kTree.setTree("K");
		
		BinaryTreeInterface<String> eTree = new BinaryTree<String>();
		eTree.setTree("E",jTree,kTree);
		
		BinaryTreeInterface<String> bTree = new BinaryTree<String>();
		bTree.setTree("B",dTree,eTree);
		
		
		BinaryTreeInterface<String> lTree = new BinaryTree<String>();
		lTree.setTree("L");
		BinaryTreeInterface<String> mTree = new BinaryTree<String>();
		mTree.setTree("M");
		BinaryTreeInterface<String> gTree = new BinaryTree<String>();
		gTree.setTree("G",lTree,mTree);
		
		BinaryTreeInterface<String> fTree = new BinaryTree<String>();
		fTree.setTree("F");
		
		BinaryTreeInterface<String> cTree = new BinaryTree<String>();
		cTree.setTree("C",fTree,gTree);
		
		BinaryTreeInterface<String> aTree = new BinaryTree<String>();
		aTree.setTree("A",bTree,cTree);
		
		((BinaryTree<String>)aTree).preorderTraverse();

返回结果：

A B D H I E J N O K C F G L M

可见我们的算法是正确的。

中序遍历迭代版本的分析及实现：

和前序遍历相似，中序遍历只不过是先不访问节点，而是遍历左子树。在前序遍历中我们在栈中存储的是各子树根节点的右节点，在这里为了先不打印根节点，我们将其放入栈中，具体的思想和上面的类似，直接看代码：

private void traversePartInorder(BinaryNode<T> rootNode,
			Stack<BinaryNode<T>> stack) 
		BinaryNode<T> currentNode = rootNode;
		while (currentNode != null) 
			stack.push(currentNode);
			currentNode = currentNode.getLeftChild();
		
	

public void inorderTraverse() 
		Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
		BinaryNode<T> rightNode = root;
		while (true) 
			traversePartInorder(rightNode, stack);
			if (stack.isEmpty()) 
				break;
			
			BinaryNode<T> currentNode = stack.pop();
			System.out.println(currentNode.getData());
			rightNode = currentNode.getRightChild();
		
	

具体原理和上面的类似，就不再赘述了。下面是测试代码和返回结果：

((BinaryTree<String>)aTree).inorderTraverse();

返回结果：

H D I B N J O E K A F C L G M 

后序遍历迭代版本的分析及实现：

后序遍历稍微有一些复杂，有需要将左右孩子节点都入栈的地方，代码相对来说更清晰一些：

private void traversePartPostorder(BinaryNode<T> rootNode,
			Stack<BinaryNode<T>> stack) 
		BinaryNode<T> currentNode = rootNode;
		while (currentNode != null) 
			if(currentNode.getLeftChild() != null)
				//当前节点有左孩子
				if(currentNode.getRightChild() != null)
					//如果当前节点有右孩子优先让右孩子进入
					stack.push(currentNode.getRightChild());
				
				stack.push(currentNode.getLeftChild());
			else
				stack.push(currentNode.getRightChild());
			
			
			currentNode = stack.peek();
		
		//将最后放进去的空节点弹出
		stack.pop();
	

public void postorderTraverse() 
		Stack<BinaryNode<T>> stack = new Stack<BinaryNode<T>>();
		BinaryNode<T> currentNode = root;
		if(currentNode != null)
			stack.push(currentNode);
		
		while(!stack.isEmpty())
			if((stack.peek().getLeftChild() != currentNode) && (stack.peek().getRightChild() != currentNode))
				traversePartPostorder(stack.peek(),stack);
			
			currentNode = stack.pop();
			System.out.println(currentNode.getData());
		
	

测试代码：

((BinaryTree<String>)aTree).postorderTraverse();

测试结果：

H I D N O J K E B F L M G C A