深度学习Deep Learning（04）：权重初始化问题2_ReLu激励函数

Posted 2022-12-10 莫失莫忘Lawlite

• github地址：https://github.com/lawlite19/DeepLearning_Python

三、权重初始化问题2_ReLu激励函数

1、说明

• 参考论文：https://arxiv.org/pdf/1502.01852v1.pdf
• 或者查看这里，我放在github上了：https://github.com/lawlite19/DeepLearning_Python/blob/master/paper/Delving%20Deep%20into%20Rectifiers%20Surpassing%20Human-Level%20Performance%20on%20ImageNet%20Classification%EF%BC%88S%E5%9E%8B%E5%87%BD%E6%95%B0%E6%9D%83%E9%87%8D%E5%88%9D%E5%A7%8B%E5%8C%96%EF%BC%89.pdf

2、ReLu/PReLu激励函数

• 目前ReLu激活函数使用比较多，而上面一篇论文没有讨论，如果还是使用同样初始化权重的方法（Xavier初始化）会有问题
• PReLu函数定义如下：
  
  • 
  • 等价于：
• ReLu（左）和PReLu（右）激活函数图像
  

3、前向传播推导

• 符号说明
  
  • ε……………………………………目标函数
  • μ……………………………………动量
  • α……………………………………学习率
  • f()………………………………激励函数
  • l……………………………………当前层
  • L……………………………………神经网络总层数
  • k……………………………………过滤器filter的大小
  • c……………………………………输入通道个数
  • x……………………………………k^2c*1的向量
  • d……………………………………过滤器filter的个数
  • b……………………………………偏置向量
• ……………………………………………………..(1)
  
  • 
  • 
• 根据式(1)得：
  …………………………………………..(2)
• 因为初始化权重w均值为0，所以期望：，方差：
• 根据式(2)继续推导：
  ……………………………………..(3)
  
  • 对于x来说：，除非x的均值也是0,
  • 对于ReLu函数来说：，所以不可能均值为0
• w满足对称区间的分布，并且偏置，所以也满足对称区间的分布，所以：
  ……………………………………(4)
• 将上式(4)代入(3)中得：
  ……………………………………………….(5)
• 所以对于L层:
  ……………………………………………………………(6)
  
  • 从上式可以看出，因为累乘的存在，若是，每次累乘都会使方差缩小，若是大于1，每次会使方差当大。
  • 所以我们希望：
    
• 所以初始化方法为：是w满足均值为0，标准差为的高斯分布，同时偏置初始化为0

4、反向传播推导

• …………………………………………….(7)
  
  • 假设和相互独立的
  • 当初始化Wie对称区间的分布时，可以得到：的均值为0
  • △x,△y都表示梯度，即：
    ，
• 根据反向传播：
  
  
  • 对于ReLu函数，f的导数为0或1，且概率是相等的，假设和是相互独立的，
  • 所以：
• 所以：……………………………………………(8)
• 根据(7)可以得到：
  
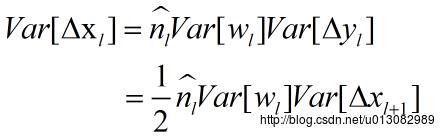
• 将L层展开得：
  …………………………………………………..(9)

• 同样令：

  • 注意这里：，而

• 所以应满足均值为0，标准差为：的分布

5、正向和反向传播讨论、实验和PReLu函数

• 对于正向和反向两种初始化权重的方式都是可以的，论文中的模型都能够收敛
• 比如利用反向传播得到的初始化得到：

• 对应到正向传播中得到：
  

• 所以也不是逐渐缩小的

• 实验给出了与第一篇论文的比较，如下图所示，当神经网络有30层时，Xavier初始化权重的方法（第一篇论文中的方法）已经不能收敛。
  
• 对于PReLu激励函数可以得到：
  
  • 当a=0时就是对应的ReLu激励函数
  • 当a=1是就是对应线性函数