数据挖掘2021期末复习考试重点大纲

Posted 2022-12-10 Rose J

本文目录

• • 1.欧几里得距离的计算
  • • • 1.二维空间的公式
      • 2.三维空间的公式
      • 3.n维空间的公式
  • 2.余弦相似度的计算
  • • • 1.二维空间的公式
      • 2.n维空间的公式
  • 3.简单匹配系数的计算
  • 4.Jaccard相似系数的计算
  • 5.性能度量准确率和错误率
  • 6.数据集的Classification Error和GINI值
  • 7. 召回率和精度的计算
  • 8.问答题
  • • 1.简述支持向量机的“最大边缘”原理。
    • 2.简述软边缘支持向量机的基本工作原理。
    • 3.简述非线性支持向量机的基本工作原理。
  • 9.计算题
  • • 1、朴素贝叶斯分类
    • 2、ID3决策树，计算数据集的熵，计算划分的期望信息、信息增益
    • 3、计算欧氏距离、KNN分类
    • 4、给定事务数据集，求频繁k项集，求指定的关联规则的支持度和置信度

1.欧几里得距离的计算

欧几里得距离在二维空间里，就是高中学的两点之间的最短距离，也就是直线距离 的求法，三维空间就是加上z轴坐标，一样的道理

1.二维空间的公式

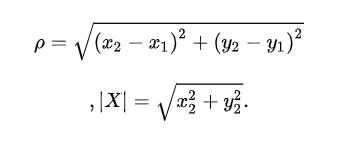
2.三维空间的公式

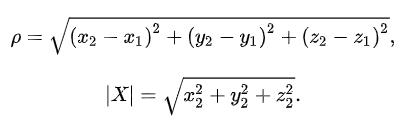
3.n维空间的公式

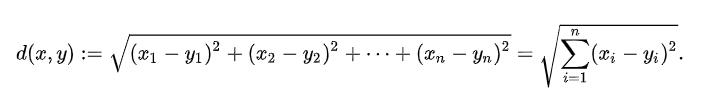
2.余弦相似度的计算

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。

1.二维空间的公式

在向量表示的三角形中，假设a向量是（x1, y1），b向量是(x2, y2)，那么可以将余弦定理改写成下面的形式：

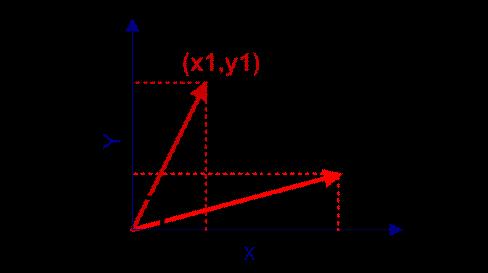
向量a和向量b的夹角 的余弦计算如下

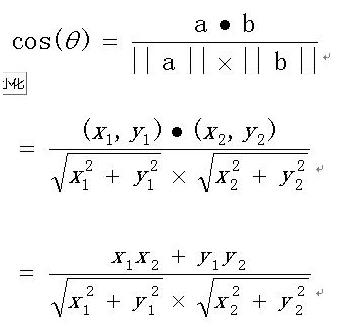
2.n维空间的公式

如果向量a和b不是二维而是n维，上述余弦的计算法仍然正确。假定a和b是两个n维向量，a是 ，b是 ，则a与b的夹角 的余弦等于：

余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，夹角等于0，即两个向量相等，这就叫"余弦相似性"。

————————————————————————————————————

例题：

向量A：(1，1，2，1，1，1，0，0，0)

向量B：(1，1，1，0，1，1，1，1，1)

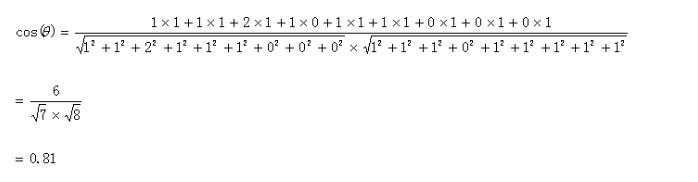
3.简单匹配系数的计算

定义：

简单匹配系数（simple matching coefficient）的定义如下：

设x和y是两个对象，都有n个二元属性组成。这两个对象（二元向量）进行比较，可以生成4个量：

f00=x取0且y取0的属性个数；
f10=x取1且y取0的属性个数；
f01=x取0且y取1的属性个数；
f11=x取1且y取1的属性个数；

SMC=值匹配的属性个数/属性个数

​ =(f11+f00)/(f01+f10+f00+f11)

————————————————————————————————————

例题：

smc=2/5=0.4

4.Jaccard相似系数的计算

定义：

给定两个集合A,B，Jaccard 系数定义为A与B交集的大小与A与B并集的大小的比值，定义如下：

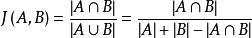
当集合A，B都为空时，J(A,B)定义为1。

主要用于计算符号度量或布尔值度量的个体间的相似度，因为个体的特征属性都是由符号度量或者布尔值标识，因此无法衡量差异具体值的大小，只能获得“是否相同”这个结果，所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。

————————————————————————————————————

与Jaccard 系数相关的指标叫做Jaccard 距离，用于描述集合之间的不相似度。Jaccard 距离越大，样本相似度越低。公式定义如下：

其中对参差（symmetric difference）

————————————————————————————————————

例题：

1、如果比较X与Y的Jaccard相似系数，只比较xn和yn中相同的个数，公式如下：
如集合A=1,2,3,4;B=3,4,5,6;
那么他们的J(X,Y)=13,4/11,2,3,4,5,6=1/3;

2、样本A与样本B是两个n维向量，而且所有维度的取值都是0或1。例如：A(0111)和B(1011)。我们将样本看成是一个集合，1表示集合包含该元素，0表示集合不包含该元素。

概念浅析：假设A是坚果Pro2 , B是 苹果8x。 为了比较两个手机，给出了n个评价指标，即n维特征，也就是n维向量：1-是国产、2-有刘海、3-价格高于5000。那么对于A=（100），B=（011）。所以，n维向量指样本的N维特征，组成一个集合。而集合是由元素组成的，在对应的特征位置，如果样本有该特征，这个位置集合值取1，表示包含该元素；否则，取0，表示不包含该元素。可见，元素=特征。

P：样本A与B都是1的维度的个数（表示都有）

q：样本A是1，样本B是0的维度的个数（表示A有,B没有）

r：样本A是0，样本B是1的维度的个数（表示A没有,B有）

s：样本A与B都是0的维度的个数（表示都没有）…0

那么样本A与B的杰卡德相似系数可以表示为：

这里p+q+r可理解为A与B的并集的元素个数，而p是A与B的交集的元素个数。

而样本A与B的杰卡德系数表示为：

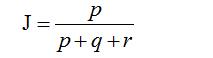
5.性能度量准确率和错误率

分类（classification）分类任务就是通过学习得到一个目标函数分，把每个属性集x映射到一个预先定义的类标号y。

————————————————————————————————————

下表中描述二元分类问题的混淆矩阵，表中每个表项fij表示实际类标号为i但被预测为j的记录数，例如，f01原本表示属于类0但被误分为类1的记录数，按照混淆矩阵中的表项，被分类模型正确预测的样本总数是（f11+f00），而被错误预测的样本总数是（f01+f10）

虽然混淆矩阵提供衡量分类模型性能的信息，但是用一个数汇总这些信息更便于比较不同模型的性能，为实现这一目的，可以使用性能度量（准确率和错误率）。

如准确率：
$$准确率=正确预测数/预测总数=（f11+f00）/（f11+f10+f01+f00）$$
错误率：
$$错误率=错误预测数/预测总数=（f10+f01）/（f11+f10+f01+f00）$$

6.数据集的Classification Error和GINI值

​

选择最佳划分的度量通常是根据划分后子女节点不纯性的程度，不纯的程度越低，类分布就越倾斜。例如，类分布为（0，1）具有不纯性，而均衡分布（0.5,0.5）的结点具有最高的不纯性。不纯性度量的例子包括：

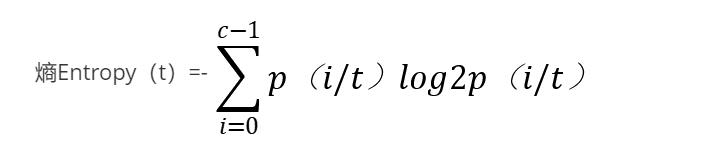
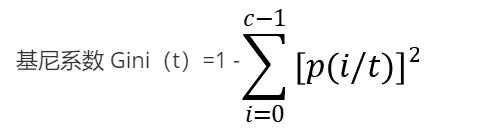
其中c是类的个数，并且在计算熵时，Olog20=0.

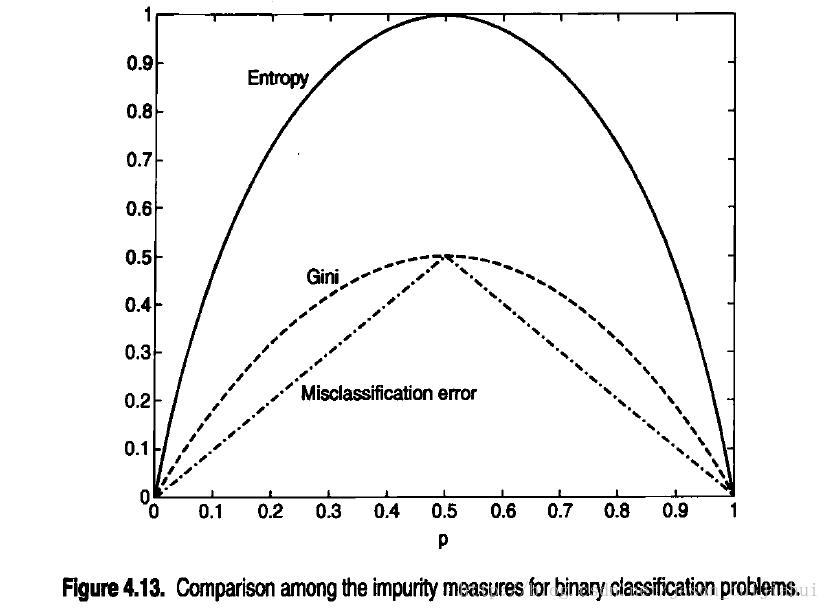
上图显示了二元分类问题不纯性度量值的比较，p表示属于其中一个类的记录所占的比例，从图中可以看出，三种方法都在类分布均衡时（即当p=0.5时）达到最大值，而当所有记录都属于同一个类时（p等于1或0）达到最小值。

下面给出三种不纯性度量的计算实例

结点N1	计数
类=0	0
类=1	6

Gini=1-(0/6)²-(6/6)²=0

Entropy= -(0/6)log2(0/6)-(6/6)log2(6/6)=0

Error=1-max[0/6,6/6]=0

结点N2	计数
类=0	1
类=1	5

Gini=1-(1/6)²-(5/6)²=0.278

Entropy= -(1/6)log2(1/6)-(5/6)log2(5/6)=0.650

Error=1-max[1/6,5/6]=0.167

结点N3	计数
类=0	3
类=1	3

Gini=1-(3/6)²-(3/6)²=0.5

Entropy= -(3/6)log2(3/6)-(3/6)log2(3/6)=1

Error=1-max[3/6,3/6]=0.5

7. 召回率和精度的计算

类不是同等重要的二类分类问题的混淆矩阵

在谈到混淆举证列出的计数时，经常用到下面的术语、

• 真正(TP)或f++，对应被分类模型正确预测的正样本数

• 假负(FN)或f±，对应于被分类模型错误预测为负类的正样本数

• 假正(FP)或f-+，对应被分类模型错误预测为正类的负样本数

• 真负(TN)或f–，对应于被分类模型正确预测的负样本数

召回率和精度是两个广泛使用的度量，用于成功预测一个类比预测其他类更加重要的应用，下面给出精度§和召回率®的形式化定义

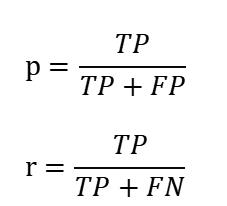
精度确定在分类器断言为正类的那部分记录中实际为正类的记录所占的比例。精度越高，分类器的假正类错误率就越低。

召回率度量被分类器正确预测的正样本的比例，具有高召回率的分类器很少将正样本误分为负样本，实际上，召回率的值等于真正率。

8.问答题

1.简述支持向量机的“最大边缘”原理。

“最大边缘”原理：即追求分类器的泛化能力最大化。即希望所找到的决策边界，在满足将两类数据点正确的分开的前提下,对应的分类器边缘最大。这样可以使得新的测试数据被错分的几率尽可能小。

2.简述软边缘支持向量机的基本工作原理。

软边缘(soft margin)SVM的基本工作原理：
对存在数据污染、近似线性分类的情况,可能并不存在一个最优的线性决策超平面；当存在噪声数据时，为保证所有训练数据的准确分类， 可能会导致过拟合。因此，需要允许有一定程度“错分”,又有较大分界区域的最优决策超平面，即软间隔支持向量机。
软间隔支持向量机通过引入松弛变量、惩罚因子，在一定程度上允许错误分类样本，以增大间隔距离。在分类准确性与泛化能力上寻求一个平衡点。

3.简述非线性支持向量机的基本工作原理。

对非线性可分的问题，可以利用核变换，把原样本映射到某个高维特征空间，使得原本在低维特征空间中非线性可分的样本，在新的高维特征空间中变得线性可分，并使用线性支持向量机进行分类。

9.计算题

1、朴素贝叶斯分类

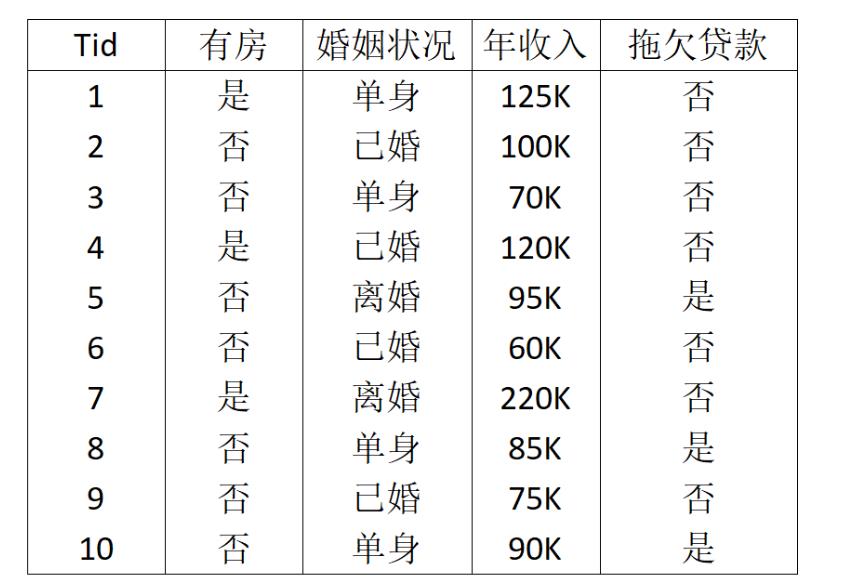
5-10贷款分类问题的朴素贝叶斯分类器

为了预测测试记录X=(有房=否，婚姻状况=已婚，年收入=$120K)的类标记，需要计算后验概率P(No/X)和P(Yes/X)。

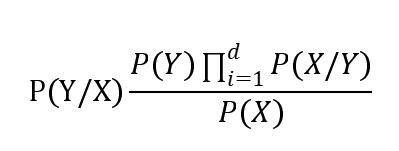
每个类的先验概率可以通过计算属于该类的训练记录所占的比例来估计。因为有3个记录属于类Yes，7个记录属于类No，所以P(Yes)=0.3,P(No)=0.7,使用图5-10中的信息。

估计分类属性的条件概率：

对分类属性Xi，根据类y中属性值等于Xi的训练实例的比例来估计条件概率P(Xi=xi/Y=y)。例如：在上图给出的训练集中，还清贷款的7个人中，3个人有房，因此条件概率P(有房=是/No)=3/7。

估计连续属性的条件概率

假设连续变量服从某种概率分布，接着使用训练样本估计分布的参数，高斯分布通常被用来表示连续属性的类条件概率分布。高斯分布有2个参数，均值 μ和方差 σ ²，对于每个类 yi ，属性 Xi 的类条件概率为：

类条件概率计算如下：

s²=（（125-110）²+（100-110）²+…+(75-110)²）/7=2975(方差)

s=54.54（标准差）

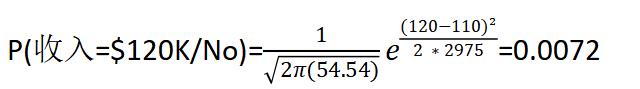
P(No/X)=P(有房=否/No) X P(婚姻状况=已婚/No) X P(年收入=$120K/No)

​ =4/7 x 4/7 x 0.0072

​ =0.0024

放到一起可得到类No的后验概率P(No/X)=α x 7/10 x 0.0024 =0.0016α，其中 α=1/P(X)是个常量。

同理，可以得到类Yes的后验概率等于0.因为它的类条件概率等于0，因为它的类条件概率等于0。

因为P(No/X)>P(Yes/X),所以记录分类为No。

————————————————————————————————————

2、ID3决策树，计算数据集的熵，计算划分的期望信息、信息增益

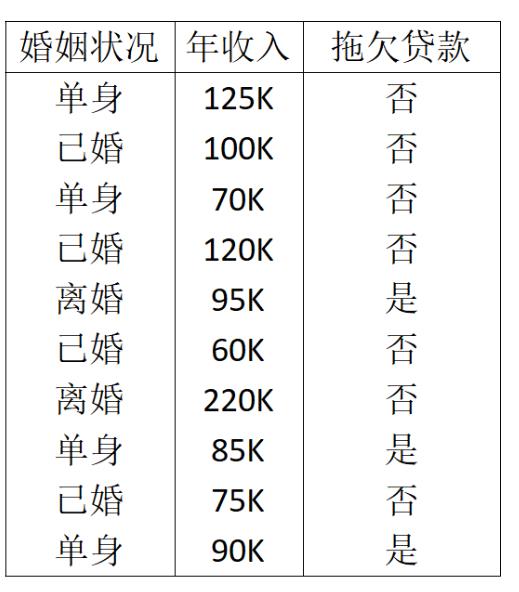
(1)该数据中：

P(Yes)=0.3

P(No)=0.7

Info(D)=I(3,7)

（2）若以婚姻状况为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应D1=已婚，D2=离婚，D3=单身。三个子集的样本数量与原始数据集的比例分别为0.4、0.2、0.4

（3）若以婚姻状况为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应婚姻状况1=已婚，婚姻状况2=离婚，婚姻状况3=单身。三个子集的熵分别为 I(0,4)、I(1,1)、I(2,2)

4）若以婚姻状况为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应婚姻状况1=已婚，婚姻状况2=离婚，婚姻状况3=单身。该划分的期望信息为 (4/10) I(0，4)+(1/5) I(1，1)+(2/5)I(2，2)*

（5）若以婚姻状况为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应婚姻状况1=已婚，婚姻状况2=离婚，婚姻状况3=单身。。该划分的信息增益为*I(3,7)- (4/10)* I(0，4)+(1/5)* I(1，1)+(2/5)I(2，2)

3、计算欧氏距离、KNN分类

（1）已知有5个训练样本，分别为
样本1，属性为：[2,0,2] 类别 0
样本2，属性为：[1,5,2] 类别 1
样本3，属性为：[3,2,3] 类别 1
样本4，属性为：[3,0,2] 类别 0
样本5，属性为：[1,0,6] 类别 0

有1个测试样本，属性为：[1,0,2]

1、测试样本到5个训练样本（样本1、2、3、4、5）的欧氏距离依次为：1、5、3、2、4

2、K=3，距离测试样本最近的k个训练样本依次为：样本1、样本4、样本3

3、距离最近的k个训练样本类别依次为：类别0、类别0、类别1

4、KNN算法得到的测试样本的类别为：类别0

4、给定事务数据集，求频繁k项集，求指定的关联规则的支持度和置信度

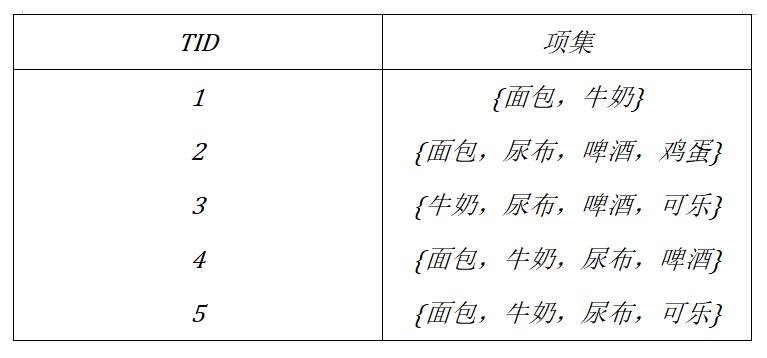
购物篮事务的例子

在关联分析中，包含0个或多个项的集合称为项集。如果一个项集包含k个项。则称它为k-项集。例如，面包，尿布，啤酒，鸡蛋，是一个4-项集。空集是指不包含任何项的项集

例：

考虑规则牛奶，尿布–>啤酒，由于项集牛奶，尿布，啤酒的支持度计数是2，而事务的总数是5，所以规则的支持度为2/5=0.4。

规则的置信度是项集牛奶，尿布，啤酒的支持度计数与项集牛奶，尿布支持度计数的商，由于存在3个事务同时包含牛奶和尿布，所以该规则的置信度为2/3=0.67