[NOI2013]向量内积

Posted 2022-12-09 ZLTJohn

题目描述

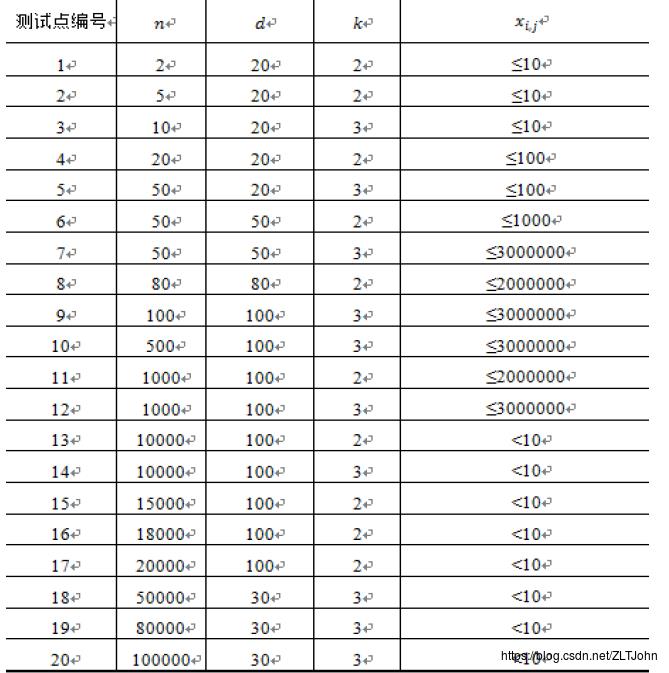
解题思路

发现k只有2和3，我们先考虑2怎么做。
转化一下，考虑原本的n个向量，我们把它写成一个n*d的矩阵$A$，然后再转置矩阵变成$A^T$，再$A*A^T$，得出矩阵$B$，那么$B_i,j$代表第i个向量和j的点积的值。那么现在问题变成B矩阵除了对角线是不是全是1。当然…现在直接做依然是$O(n^2d)$的

一种判断两个矩阵是否相等的方法是，设随机向量$v$，若$v*A=v*B$，那么可能有$A=B$，正确率大概是1/2，当然，不相等那就肯定不等了。

怎么使用这个东西呢？假设我们知道$A*A^T$，那么如果不存在一对可行解，那么$A*A^T$除了对角线全是1。我们设随机向量v（1*n的向量），O(nd)地算出$v*A*A^T$，设为$av$；再设$C$为对角线和$A*A^T$相同，其余位置全为1的矩阵，算出$bv=v*C$，这个由于C是除对角线的全一矩阵，所以O(n)就可以算出来，具体地，我们可以先当成全1矩阵算，再消去对角线影响。
此时，如果两个向量一样，那么可能A=B，如果不一样，就出解了，不一样的那一位，就是可行点对中的其中一个，然后我们枚举其他向量和他组合找到答案即可。
一样的话还要随机多几次，大概10次以上就够了。

矩阵乘法基础知识

我太菜了…实现都不会
注意到$a\\times b的矩阵和b\\times c$的矩阵乘起来是$a\\times c$的矩阵，向量相当于一个$1\\times n$或者$n\\times 1$的矩阵。
然后矩阵乘法的时候，我们知道最终矩阵的大小，然后枚举这个大小的两维，再枚举一个循环来做乘法即可。
然后寻址优化一下。

k=3怎么做？

考虑到此时有可能有2，就不能搞全1矩阵了。此时，我们考虑把$A*A^T和C$最终的每一位都平方一下，那么最终矩阵的2就没有了，此时，我们要对$A和A^T$做一些改变，才能让上面的方法搞出来的意义是平方后的结果。
考虑到两个向量点积的平方的式子：$(\\sum_i=1..da_ib_i)^2=\\sum_i=1..d\\sum_j=1..da_ia_jb_ib_j$，那么我们可以把原向量看成长度为d*d的向量，具体地$newa_(i-1)*d+j=a_i*a_j$，然后这样我们再套用上面的算法即可。

代码

#include<cstdio> 
#include<algorithm>
#include<cstring>
#include<cmath>
#include<map>
//¿ª O2£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡£¡ 
using namespace std;
#define fo(i,j,k) for(i=j;i<=k;i++)
#define fd(i,j,k) for(i=j;i>=k;i--)
#define cmax(a,b) (a=(a>b)?a:b)
#define cmin(a,b) (a=(a<b)?a:b)
typedef long long ll;
typedef long long LL;
typedef double db;
const int N=1e5+5,D=105;
int a[N][D],c[N],v[N],v1[N],v2[N],sum,seed,TT,i,j,k,l,n,d,K;
void get(int x)

    fo(i,1,n) if (i!=x)
    
        sum=0;
        fo(j,1,d) sum=(sum+a[i][j]*a[x][j])%K;
        if (!sum)
        
            if (x>i) swap(x,i);
            printf("%d %d\\n",x,i);
            exit(0);
        
    

int main()

    freopen("3.in","r",stdin);
//  freopen("3.out","w",stdout);
    scanf("%d %d %d",&n,&d,&K);
    fo(i,1,n) 
        fo(j,1,d)
        
            scanf("%d",a[i]+j);
            seed=seed^a[i][j];
            a[i][j]%=K;
        
    if (K==2) fo(i,1,n) 
    
        fo(j,1,d) c[i]=(c[i]+a[i][j]*a[i][j]);
        c[i]%=K;
    
    else fo(i,1,n) 
    
        fo(j,1,d) c[i]=(c[i]+a[i][j]*a[i][j]);
        c[i]=c[i]*c[i]%K;
     
    srand(seed);
    fo(TT,1,6)
    
        sum=0;
        fo(i,1,n) v[i]=rand()%K,sum+=v[i];
        sum%=K;
        // vc[1~n]=sum
        if (K==2)
        
            fo(j,1,d) v1[j]=0;
            fo(i,1,1)
                fo(k,1,n)
                    fo(j,1,d)
                        v1[j]=v1[j]+v[k]*a[k][j];
            fo(j,1,d) v1[j]%=K;
            fo(j,1,n) v2[j]=0;
            fo(i,1,1)
                fo(j,1,n)
                    fo(k,1,d)
                        //v2[j]=(v2[j]+v1[k]*a[k][j])%K;
                        v2[j]=v2[j]+v1[k]*a[j][k];
        else
        
            fo(j,1,d*d) v1[j]=0;
            fo(i,1,1)
                fo(k,1,n)
                    fo(j,1,d)
                        fo(l,1,d)
                            v1[(j-1)*d+l]=v1[(j-1)*d+l]+v[k]*a[k][j]*a[k][l];
            fo(j,1,d*d) v1[j]%=K;
            fo(j,1,n) v2[j]=0;
            fo(i,1,1)
                fo(j,1,n)
                    fo(k,1,d)
                        fo(l,1,d)
                        //v2[j]=(v2[j]+v1[(k-1)*d+l]*a[k][j]*a[k][l])%K;
                        v2[j]=v2[j]+v1[(k-1)*d+l]*a[j][k]*a[j][l];
        
        fo(i,1,n) v2[i]=(v2[i]+(1-c[i])*v[i]+K)%K;
        fo(i,1,n) if (v2[i]!=sum) get(i);
    
    printf("-1 -1\\n");