机器学习-神经网络（Neural Network）算法

Posted 2022-12-09 YEN_csdn

学习彭亮《深度学习基础介绍：机器学习》课程

背景

以人脑中的神经网络为启发，最著名的算法是1980年的backpropagation

多层向前神经网络（Multilayer Feed-Forward Neural Network）

1. Backpropagation被使用在多层向前神经网络上
2. 多层向前神经网络由以下几部分组成：输入层（input layer）、隐藏层（hidden layer）、输出层（output layers）
3. 每层又单元组成
4. 输入层是由训练集的实例特征向量传入
5. 经过连接结点的权重传入下一层，一层的输出是下一层的输入
6. 隐藏层的个数可以是任意的，输入层有一层，输出层有一层
7. 每个单元（unit）也可以被作为神经结点，根据生物学来源定义
8. 一层中加权的求和，然后根据非线性方程转化输出
9. 作为多层向前神经网络，理论上，如果有足够多的隐藏层和足够大的训练集，可以模拟任何方程

设计神经网络结构

1. 使用神经网络训练数据之前，必须确定神经网络层数，以及每层单元的个数
2. 特征向量在被传入输入层时通常被先标准化(normalize)到0-1之间
3. 离散型变量可以编码为每一个输入单元对应一个特征值可能赋的值
   eg:特征值A可能取a0,a1,a2,可以使用3个输入单元来代表A
   如果A=a0,那么代表a0的单元值就取1，其他取0
   如果A=a1,那么代表a1的单元值就取1，其他取0

4. 神经网络即可以用来做分类（classsification）问题，也可以解决回归（regression）问题
   对于分类问题，如果是两类，可以用一个输出单元表示，如果多于两类，每一类用一个输出单元表示；
   没有明确的规则来设计最好多少个隐藏层，需要根据实验和误差，以及准确度来实验并改进

   交叉验证方法(Cross-Validation)

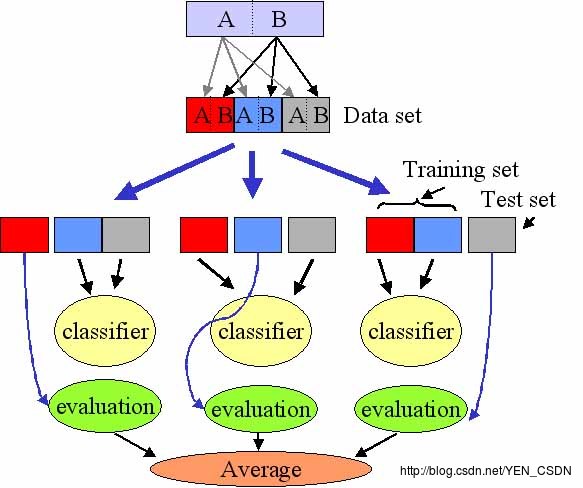
K-fold Cross Validation

Backpropagation算法

1. 通过迭代性的来处理训练集中的实例
2. 对比经过神经网络后输入层预测值(predicted value)与真实值(target value)之间
3. 反方向（从输出层=>隐藏层=>输入层）来以最小化误差(error)来更新每个连接的权重(weight)

算法详细介绍

输入：D：数据集，l 学习率(learning rate)， 一个多层前向神经网络
输出：一个训练好的神经网络(a trained neural network)

初始化权重(weights)和偏向(bias): 随机初始化在-1到1之间，或者-0.5到0.5之间，每个单元有一个偏向

###对于每一个训练实例X，执行以下步骤：

1. 由输入层向前传送
   
   
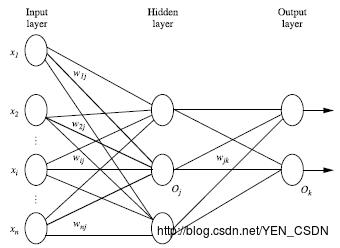
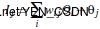
   wij：i、j连线上的权重
   Oi：前一次那个单元的值是多少
   Θj：偏向
   
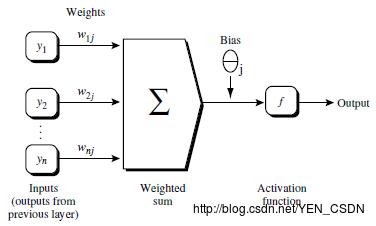
   y1*w1j+ y2*w2j+ y3*w3j+Θj
   

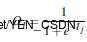
2. 根据误差(error)反向传送
   输入层：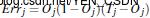

   隐藏层：
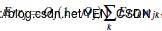
   权重更新：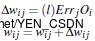
   偏向更新：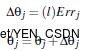

3. 终止条件
   权重的更新低于某个阈值；
   预测的错误率低于某个阈值；
   达到预设一定的循环次数

Backpropagation 算法举例

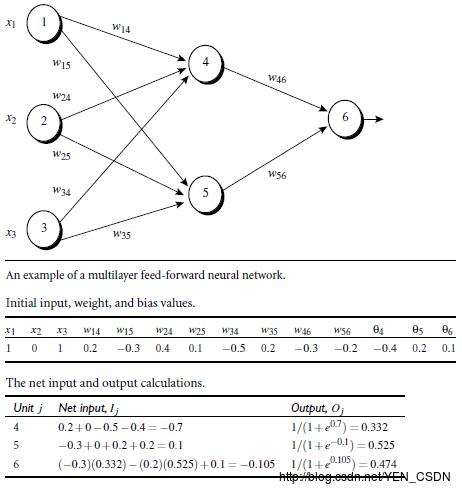
每两条线都有一个权重:Wij,eg：w15表示点1，5权重为-0.3
Θ4：4对应的偏向为-0.4

计算O4：

x1*w14+x2*w24+x3*w34+Θ4=1*0.2+0*0.4+1*(-0.5)+(-0.4)=-0.7

同理计算O5、O6

---

按照上面的计算说明：

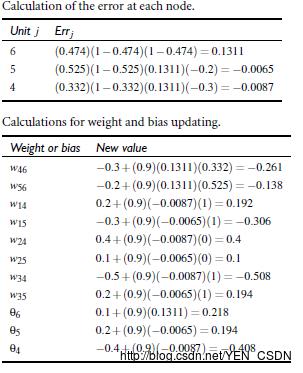
输出层：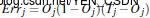
Tj是训练层里给的，假设他为1，则

Err(6)=(0.474)(1-0.474)(1-0.474)=0.1311

同理Err(5)、Err(4)

---

隐藏层：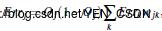

Err(5)=0.525*（1-0.525）*（0.1311）*（-0.2）=-0.0065
（0.1311）：6这一结点的误差
（-0.2）：5、6之间的权重
同理
Err(4)=0.332*（1-0.332）*（0.1311）*（-0.3）=-0.0087
（0.1311）：6这一结点的误差
（-0.3）：4、6之间的权重

权重和偏向的更新

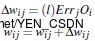
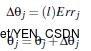
w46=-0.3+（0.9）*（0.1311）*（0.332）=-0.261
l:学习率，手动定义，此处假设为0.9 


Θ4=-0.4+（0.9）（-0.0087）=-0.408