逆向-除法优化上

Posted 2022-12-09 嘻嘻兮

上一篇说完加减乘的优化，这篇来说说除法，首先先打个铺垫，除法的优化涉及到各种数学公式，这里我们主要探讨一下结论，具体的证明可以参考《C++反汇编与逆向分析技术揭秘》，这里做一个总结。

首先，如果除数为变量时，是没有任何的优化空间的，所以老老实实的上对应的汇编代码即可，所以就不讨论了。下面主要来讨论下除数为常量的情况，并且这个常量还是正数，负数情况下一篇博客介绍。

首先，先来看一下需要讨论的情况

除数为常量-除数为正数情况
    1.除数为2的幂-被除数无符号
    2.除数为2的幂-被除数有符号
    3.除数为非2的幂 - 被除数无符号	
    	根据Magic Number的是否需要进位(下面简称M)
            3.1 M值无进位
            3.2 M值有进位
    4.除数为非2的幂 - 被除数有符号
    	根据Magic Number的正负情况(下面简称M)
            4.1 M值为正数
            4.2 M值为负数

这个情况是有那么点多，不过其实总体算下来，应该就两套公式，分别为除数为2的幂和除数为非2的幂两套，只是情况不同，有些公式的变种而已。还有对于Magic Number这个概念，后面会提的，这里留个先个印象就好

首先，先来打一些基础的铺垫

1.乘法有无符号混合为有符号乘法（IMUL）
2.除法有无符号混合为无符号除法（DIV）
3.计算机中的除法为向零取整
4.移位运算是向下取整(不大于的关系)

首先对于向上取整和向下取整，对于计算机的同学应该十分熟悉了，其实对于向零取整其实就是往中间的零值靠齐

3 / 2 = 1.5   //往零靠齐取1    3/2=1
-3 / 2 = -1.5 //往零靠齐取-1  -3/2=-1

还有对于第四点一定要理解，因为在下面会有用到，移位运算，这里说的更细一点吧，对于除法需要用到的就是右移运算，你可以这样想，当二进制往右移动，那么肯定有一些位需要丢失，那么肯定是不大于的关系。

假设我们需要计算-5/2,那么我们很容易想到，使用右移一位，那么如下结果计算出来为-3（因为向下取整的原因），如果此时可以向上取整（向零取整），那么就符合我们的数学运算结果了。

-5>>1
FFFFFFFB     >> 1
.......1011  >> 1
.......1101  -> FFFFFFFD = -3

首先，先来说下除数为2的幂的情况，这里我们可以使用右移，但是右移，对于负数的情况就会出现上面的问题，如下代码

	for(int i=-20;i <= 20;++i)
	
		printf("%d / 8 = %d\\r\\n",i,i/8);
		printf("%d >> 3 = %d\\r\\n\\r\\n",i,i>>3);
	 

打印运算结果，其实可以发现，在负数中的确会有问题，那么我们可以这样子来调整一下，加上n-1的值，n为除数

	for(int i=-20;i <= 20;++i)
	
		printf("%d / 8 = %d\\r\\n",i,i/8);
		if(i >= 0)
			printf("%d >> 3 = %d\\r\\n\\r\\n",i,i>>3);
		else
			printf("%d >> 3 = %d\\r\\n\\r\\n",i,(i+8-1)>>3);
	 

部分结果

-13 / 8 = -1
-13 >> 3 = -1

-12 / 8 = -1
-12 >> 3 = -1

-11 / 8 = -1
-11 >> 3 = -1

-10 / 8 = -1
-10 >> 3 = -1

此时可以发现，结果吻合了，那么为什么加上n-1呢，你可以这样子想，负数右移与实际数学运算不符合的原因是因为右移向下取整了，那么如何才能向上取整呢，其实我们先来加上一个n值，你会发现大部分情况是对的

printf("%d >> 3 = %d\\r\\n\\r\\n",i,(i+8)>>3);

不正确的情况如下：

-16 / 8 = -2
-16 >> 3 = -1

-8 / 8 = -1
-8 >> 3 = 0

当这个被除数可以整除时，这个结果就会大一，这个就应该很清楚了为啥了，那么如何避免呢，其实我们可以加上n-1的值，我们可以这样子来考虑一下

假设原先的商为q
如果可以被整除，加上 n-1,由于没有加满n，所以结果肯定还是q
如果不能被整除，加上 n-1,由于其值肯定会大于等于 (q+1) * n，所以结果为 q+1
    因为不能被整除,说明肯定有余数(>0),那么余数加上n-1后,其值肯定>=n，所以商会+1

好了，道理讲完了，其实这里已有一个论证的公式，公式如下

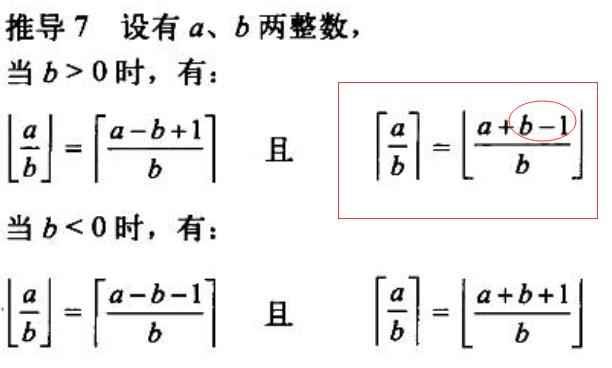
我们来看一下红框框中的那个公式，这个公式的意思的，a/b的向上取整 = 右边部分的向下取整值。

这个公式我们从右往左看，就可以发现正好满足我们的，右移向下取整调整到向上取整，如何调整呢？

也就是公式中椭圆圈中的部分，被除数加上（除数-1）值。

OK,下面我们就可以来看一下2有符号的情况了（1的情况无符号，说明都为正数，那么直接右移即可）

int main(int argc, char* argv[])

    printf("%d",argc/8);
    return 0;

首先，这里对于1和2的情况，debug和release的情况都一致，所以拿一个进行讨论其反汇编

00401298 8B 45 08             mov         eax,dword ptr [ebp+8]
0040129B 99                   cdq
0040129C 83 E2 07             and         edx,7
0040129F 03 C2                add         eax,edx
004012A1 C1 F8 03             sar         eax,3
004012A4 50                   push        eax

看完上面的汇编代码，7这个值我们应该会有印象的，用于调整(加n-1)，还有下面的右移三次也是知道的，只是奇怪的是，在我们上面的C源码中，是有if条件判断，也就是说这个公式只是用于负数情况的调整，那么这里的判断分支呢，其实这里的汇编代码做了一个无分支判断，下面具体来分析一下

00401298 8B 45 08             mov         eax,dword ptr [ebp+8]  ;取被除数

;扩展高位 if(eax >= 0)  edx=0  else edx = -1
0040129B 99                   cdq 

;and运算  if(eax >= 0)  edx=0  else edx = 0xFFFFFFFF & 7 = 7
0040129C 83 E2 07             and         edx,7  

;加上 edx if(eax >= 0)  add 0  else add 7
0040129F 03 C2                add         eax,edx

;调整完毕,进行右移取得结果
004012A1 C1 F8 03             sar         eax,3
004012A4 50                   push        eax

看完上面的代码注释，应该就明白了，对于正数而言，其调整需要加的值为0，相当于不调整，这样子就做了一个无分支判断的优化。

 

 

下面再来说一说3和4的情况吧，这里对于情况3和4而言（debug下不优化），我们来探讨一下release的情况，其基本原理其实用到的都是同一套的公式。

假设x为被除数，c为除数（该值为非2的幂），那么由如下推导

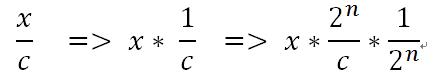
这里的推倒就毕竟容易了，首先推倒导到第一步，拿 1/c，此时会发现1和c都为常量，那么可以做常量折叠，但是一旦做了常量折叠，其结果非0即1，误差太大。所以再进行调整，调整为第三步的结构，此时n值给小了也不行，因为小了可能会存在误差。C越大n越大,编译器有一套误差规避的准则（n值又编译器确定），那么此时2^n / c就可在编译期间算出，该值为一个常量值，称为Magic Number。

那么我们设2^n/c为m,下面再来调整一下公式，使其更顺眼一点

好了，下面的变形其实最终都是围绕上面的这个式子展开的。

 

迷迷糊糊的话也没事，我们先来看3.1的情况，这是最基础的情况，基本上后面的变种都是以这种情况展开的，所以这种情况一定要理解哦。

int main(unsigned int argc, char* argv[])

    printf("%d",argc/3);
    return 0;

汇编代码如下

.text:00401000                 mov     eax, 0AAAAAAABh  ;m值
.text:00401005                 mul     [esp+argc]       ;x*m
.text:00401009                 shr     edx, 1           ;右移
.text:0040100B                 push    edx

看完上面的代码，然后再对比一下上面的公式，你会发现这段代码是不是很像套公式，首先我们先来加上如果上述代码就是公式，那么我们该如何还原呢？

1.确定右移n的数值
2.确定m的数组
2.根据公式还原

  所以当我们确定下来n和m后，只需要套用后面的公式还原c即可

好了，看上面的汇编代码，m值是很好确定的，就是0AAAAAAABh，那么n呢，是1么，显然这里肯定不是的，因为前面有说过n值不会太小，因为太小误差会太大。

x*m = edx.eax
相当于edx存储x*m的高32位
由于后面直接用了高32位的edx,相当于乘积>>32,此时再右移一位,相当于总共移动33位
.text:00401009                 shr     edx, 1           ;右移

注意,后面直接用了高32位的edx
.text:0040100B                 push    edx

所以这里的n值应该是33，上面的需要好好理解一下，因为最终使用的是edx，其实默认起步移动为32位。下面可以还原了

// 2^33 / 0AAAAAAABh  = 2.99 -> 3
// argc/3

注意这里的还原结果需向上取整即可。

 

 

下面再看一下3.2的情况，也就是M值有进位的情况

int main(unsigned int argc, char* argv[])

    printf("%d",argc/63);
    return 0;

汇编代码

.text:00401000                 mov     ecx, [esp+argc]
.text:00401004                 mov     eax, 4104105h  ;m
.text:00401009                 mul     ecx            ;x*m
.text:0040100B                 sub     ecx, edx
.text:0040100D                 shr     ecx, 1
.text:0040100F                 add     ecx, edx
.text:00401011                 shr     ecx, 5
.text:00401014                 push    ecx

看完上面的代码，估计只能分析前两句，虽然样子其实很像上面的公式，但是下面的代码不知道是干什么的，这里其实是上面的公式的一个变种，我们来根据其代码来还原一下数学表达式。

此时ecx为x(被除数),m值为4104105h，后面的公式中都用ecx和m值进行代替

首先，前三行代码很好理解

ecx * m -> edx.eax
    相乘,结果高32位存放在edx,低32位存放在eax

sub ecx,edx，说明减去的是乘积的高位    

shr ecx,1 相当于除以2                               

add ecx,edx，加上乘积高位                       

shr ecx,5 相当于除以2^5                             

好了，还原出的数学表达式就是上面的这个样子，是不是一脸的蒙蔽，这完全不像前面的基础公式，下面我们来化简一下

可以发现，对上面的式子做化简后，我们原来熟悉的模板公式就出现了，此时的M = (2^32 + m)

那么这里为什么需要加上2^32呢，因为其编译器确定的N值推理出的Magic Number大于0xFFFFFFFF，32位存放不下的缘故,相当于产生的进位，但是编译器只会控制进位一。

好了，因为此时MagicNumber存放不下，所以需要进行大数运算，为了优化除法而进行大数运算是很划不来的，所以编译器作者就对该式子进行了简而化繁(避免大数)，这里繁琐的公式也就是一开始根据汇编反推的数学公式，开始的公式里面是没有大数运算的。

好了，说到这里，m值我们就可以确定了，需要加上2^32，那么如何确定n值呢，其实看懂了上面的推导，其实可以发现这个38其实也就是数右移了多少位，再加上32即可

;....
.text:0040100D                 shr     ecx, 1
;....
.text:00401011                 shr     ecx, 5  ;该右移可有可无

下面开始还原

// 2^38 / (2^32+4104105h) = 2^38 / 4363141381 = 62.99 -> 63
// argc / 63

 

下面开始分析第4种的情况，首先来看4.1，这里位Magic Number 为正数的情况，这种情况如果前面都理解的情况下是很好理解的，相当于是前面3.1的情况，然后需要加个一个移位的分支判断，因为前面说了，右移是向下取整的，所以我们得将结果进行向上调整。

int main(int argc, char* argv[])

    printf("%d",argc/5);
    return 0;

反汇编代码

.text:00401000                 mov     ecx, [esp+argc]
.text:00401004                 mov     eax, 66666667h
.text:00401009                 imul    ecx    ;有符号
.text:0040100B                 sar     edx, 1
.text:0040100D                 mov     eax, edx  ;--
.text:0040100F                 shr     eax, 1Fh  ;--
.text:00401012                 add     edx, eax  ;--
.text:00401014                 push    edx

对比前面的3.1，就可以发现，其代码只多出了三行，也就是0D-12的那三行，这三行主要用于负数情况，需要调整向上取整，看这三行代码也是无分支的，所以也可以肯定这里用到无分支优化。那么我们还是使用上面的推导七么，这里的话很明显不是，为什么呢，因为推倒七是在移位以前做的调整，而此时调整很明显是在移位后，所以我们使用推导三的结论

这个其实也很好理解，也就是说我们右移完（下整） + 1后结果就是上整了。这里其实不理解的话可以自己带一些数值进去测试即可。

;取结果的高32位
.text:0040100D                 mov     eax, edx 
;右移动31位,相当于取符号位  if(eax >= 0) eax = 0 else eax = 1
.text:0040100F                 shr     eax, 1Fh 
; if (eax >= 0) add 0 else add 1
.text:00401012                 add     edx, eax 

好了，由于多出来的这部分是用于调整的，所以其还原的公式是与3.1一致的，下面开始还原

// 2^33 / 66666667h = 4.99 -> 5
// -> argc / 5

 

 

OK，下面分析最后一种情况，也就是当Magic Number 为负数的情况，我们先来看完汇编代码后再来细说

int main(int argc, char* argv[])

    printf("%d",argc/7);
    return 0;

反汇编代码

.text:00401000                 mov     ecx, [esp+argc]
.text:00401004                 mov     eax, 92492493h
.text:00401009                 imul    ecx
.text:0040100B                 add     edx, ecx  ;对比4.1就多出了这一行
.text:0040100D                 sar     edx, 2
.text:00401010                 mov     eax, edx
.text:00401012                 shr     eax, 1Fh
.text:00401015                 add     edx, eax
.text:00401017                 push    edx

首先，我们来看一下Magic Number，其值为92492493h，可以发现其值的确大于了0x7FFFFFFF，也就是为负数。那么说到这里其实大家可能就是有疑问了，在上面的公式意义上，Magic Number就是一个无符号数，那么现在成了负数，是不是有问题呢？

是的，问题也就是出在这里，所以我们需要解决如何将有符号数相乘转为无符号数相乘的问题？

对比4.1，其实就多出了一行代码，那么这行代码的具体什么作用呢

因为这里的有符号的情况，观察其0x401009，用到也是有符号的imul，那么在有符号数下，如果大于0x7FFFFFFF，其表示为一个负数，而对于我们之前的除法数学模型来说，x*m，这里Magic Number是一个无符号数，自然意义就不一样了。所以其实多出来的这行add edx,ecx 其实用于调整的，使其还原乘以无符号数的本意。

设有符号数为A,无符号数为M(M在有符号数下为负数)，数据宽度为WORD
neg(M) = (~M + 1)  //取反加一
neg(M) + M = ~M + 1 + M
neg(M) + M = 0xFFFF + 1
neg(M) + M = 0x10000
neg(M) = 0x10000 - M
任何数据在计算机中都是用二进制表示的，且都是用补码表示的,所以此时M的真值为 -neg(M)

A*M(有) = A*-neg(M)
        = A*-(0x10000 - M)
        = A*(M - 0x10000)
        = A*M - A*0x10000
A*M(无) = A*M
    	= A*M - A*0x10000 + A*0x10000
    	= A*M(有) + A*0x10000

如果将M作为无符号看看待,说明需要加上A*0x10000,这样子最终结果就相同了
imul reg = edx.eax
此时的edx为结果的高位,也就是10000起步,*A可调整为 edx+A
Add edx,A

所以根据上面可以得出 A*M（有） + A * 0x10000 = A * M（无）。好了因为上面验证里面的数据宽度为WORD，然后在我们的例子里是DWORD，所以我们需要加上的是 A * 2^32。

;edx = edx + ecx,也就是高32位加上ecx
;高32位加上ecx,其实也就相当于乘积加上了 ecx*2^32
.text:0040100B                 add     edx, ecx

这里的ecx也就是上面的A。总的说来，因为有符号相乘结果肯定会小，那么我们将少的这部分加上就和无符号相乘一样了。

下面我们可以使用任意一个数值来进行验证下

0x14523687 * 0x98563221 = 0xC17A7F926996567  //计算器得出

打开OD进行写入汇编验证

可以发现，其edx.eax的拼接结果与上面的计算器中运算的结果一致。

好了，明白了4.2中多出来的这行代码后，其实也就可以还原了，因为4.2对于4.1来说，也是一个调整，相当于是有符号乘调整为无符号乘，所以其基本的数学模型不变，按照4.1的方法还原即可

// 2^34 / 92492493h = 6.99 -> 7
// argc / 7