Maximum Likelihood，ML

Posted 2022-12-09 qq_784583650

Maximum Likelihood，ML（最大似然估计）

1. 问题描述（属于监督学习，已知分类）：

• 已知：训练样本已知分类的先验概率P(wi)，以及各个分类的概率密度分布；
• 所求：ML做的事情是在已知分布的情况下进行参数估计；
  

2. ML要求说明：

• 基于贝叶斯决策P(wi|x)=(P(x|wi)*P(wi))/P(x)；
• 似然函数定义：L(θ)=P(D|θ)；
• ML所做的事情是估计参数θ，使得训练集合D在已知参数θ的情况下，似然函数最大化；
• ML的想法是这个参数θ是未知的确定的，出现在D可能性最大点；
• 使用前提假设：服从什么分布，以及这些分布是独立的；（使似然函数计算方便，连乘形式）
  

3. ML在已知类别分布为高斯分布的情形下的参数估计：

• 样本集合D服从高斯分布 D~N(μ，δ^2)
  
• 对似然函数进行偏微分，估计参数θ（μ，δ^2）
• μ = 样本均值（向量，多维高斯+）；
• δ^2 = 样本协方差（矩阵，多维高斯）；

4. ML举例

使用MATLAB生成两类数据及其分布：

<span style="font-size:14px;">Sample1 = [10-rand(1,121)*40;rand(1,121)*20]';
Sample2 = [rand(1,121)*20+20;rand(1,121)*10-20]';
figure,plot(Sample2(:,1),Sample2(:,2),'*r');
hold on;
plot(Sample1(:,1),Sample1(:,2),'*');
</span>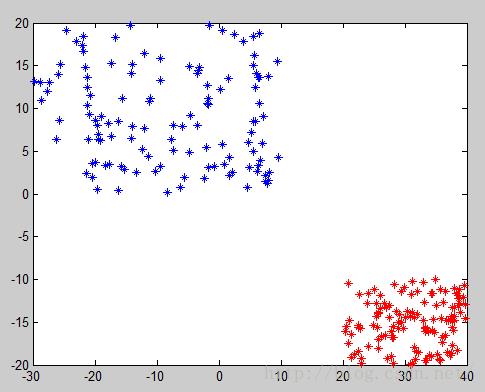

A类数据范围：[-30,10,0,20]

B类数据范围：[20,40,-20,-10]

5. 最大似然估计概率密度函数直观显示

<span style="font-size:14px;">u1=mean(Sample1);
u2=mean(Sample2);
sigm1=cov(Sample1); 
sigm2=cov(Sample2);
%计算两个样本的密度函数并显示
x= -30:0.5:40;
y= -20:0.5:20;
[X,Y] = meshgrid(x,y);
F1 = mvnpdf([X(:),Y(:)],u1,sigm1);
F2 = mvnpdf([X(:),Y(:)],u2,sigm2);
P1=reshape(F1,size(X));
P2=reshape(F2,size(X));
figure(2)
surf(X,Y,P1)
hold on
surf(X,Y,P2)
shading interp
colorbar
title('条件概率密度函数曲线');</span>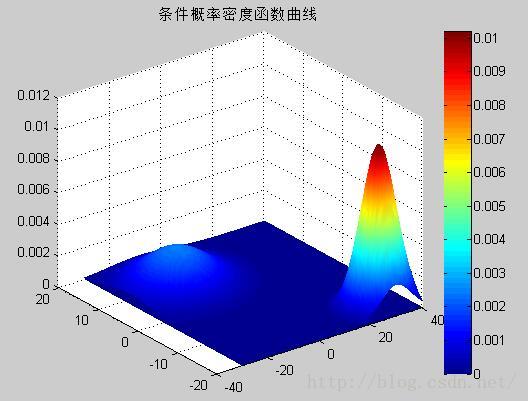

6. 绘制分类面

<span style="font-size:14px;">%用于绘制分类面
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
pw1=0.5;pw2=0.5;
figure;
for x_x = 1:81
    for y_y = 1:121
    P1_1=pw1*mvnpdf([X(x_x,y_y),Y(x_x,y_y)],u1,sigm1);
    P2_2=pw2*mvnpdf([X(x_x,y_y),Y(x_x,y_y)],u2,sigm2);   
        if(P1_1>P2_2)
             %disp('it belong to the first class');
             plot3(X(x_x,y_y),Y(x_x,y_y),P1_1,'r');
        else
             %disp('it belong to the second class');
             plot3(X(x_x,y_y),Y(x_x,y_y),P2_2,'b');
        end
     hold all
    end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%</span>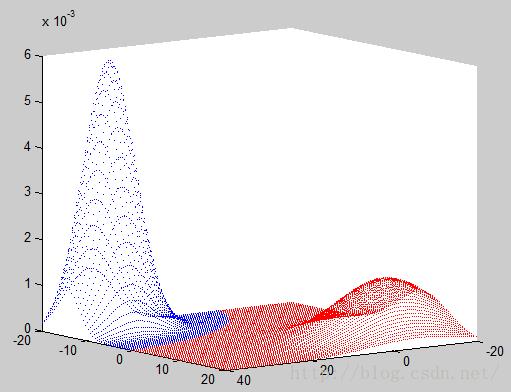

注意：这里认为先验概率都为50%

7. 完整代码

<span style="font-size:14px;">clear;
close all

%求两类训练样本的均值和方差
Sample1 = [10-rand(1,121)*40;rand(1,121)*20]';
Sample2 = [rand(1,121)*20+20;rand(1,121)*10-20]';

u1=mean(Sample1);
u2=mean(Sample2);
sigm1=cov(Sample1); 
sigm2=cov(Sample2);

%计算两个样本的密度函数并显示
x= -30:0.5:40;
y= -20:0.5:20;
[X,Y] = meshgrid(x,y);
F1 = mvnpdf([X(:),Y(:)],u1,sigm1);
F2 = mvnpdf([X(:),Y(:)],u2,sigm2);
P1=reshape(F1,size(X));
P2=reshape(F2,size(X));
figure(2)
surf(X,Y,P1)
hold on
surf(X,Y,P2)
shading interp
colorbar
title('条件概率密度函数曲线');

%用于绘制分类面
pw1=0.5;pw2=0.5;
figure;
for x_x = 1:81
    for y_y = 1:121
    P1_1=pw1*mvnpdf([X(x_x,y_y),Y(x_x,y_y)],u1,sigm1);
    P2_2=pw2*mvnpdf([X(x_x,y_y),Y(x_x,y_y)],u2,sigm2);   
        if(P1_1>P2_2)
             %disp('it belong to the first class');
             plot3(X(x_x,y_y),Y(x_x,y_y),P1_1,'r');
        else
             %disp('it belong to the second class');
             plot3(X(x_x,y_y),Y(x_x,y_y),P2_2,'b');
        end
     hold all
    end
end
</span>