计算机基础——为什么要有反码和补码，反码和补码的意义是什么

Posted 2022-12-08 iaiti

目录

1、前言，自己发明javb语言

2、模

3、先思考，为什么不能直接用源码计算

4、主角的由来

5、反应肯定是？？？

---

最近在学习一下专栏里面的数学问题，提到二进制的东西的时候，想到了大多数人在学习的时候，死记硬背上反码是怎样，补码是怎样。

现在回头问下自己，反码有何存在意义？补码有何存在意义？为什么要有反码？为什么要有补码？

1、前言，自己发明javb语言

先拿java的int 数据类型是32位，有符号的以二进制补码表示的整数；符号位为第一位，
最小值 ，第一位为1，其余为0，-2,147,483,648（-2^31) 
最大值 ，第一位为0 ，其余为1，2,147,483,647（2^31-1），是的，int型手机号码都放不下。

因为位数太长，所以以下说明的时候不太方便，假如我现在发明了了，jbvb语言，接下来整篇分析里面，

我们把int数据类型设置为4位。有符号的以二进制补码表示的整数；符号位为第一位，
最小值 ，第一位为1，其余为0，1000，（-2^3）     = -8
最大值 ，第一位为0 ，其余为1，0111,  （ 2^3 - 1）= 7

2、模

取模的除数就是数据类型的上限减去下限的值，再加上 1，也就是 (2^(n-1)-1)-(-2^(n-1))+1=2x2^(n-1)-1+1=2^n-1+1。
这个除数为什么不直接写成 2^n 呢，这是因为 2^n 已经是 n+1 位了，已经超出了 n 位所能表示的范围。
其实就是上限到下限的距离。

那这里的模是2^4 = 16 

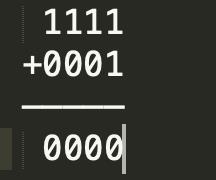
7 + 1 = 0111 + 0001 = 1000 = -8 ，上溢出，超越上限，也就是最大值+1后 会变成最小值。

还剩15的差值，-8 + 8 能回到0位置， 0+7 能回到7的位置。也就是说 7 + 模后，重新回到原来的位置。

就是余数和取模的概念，这东西周而复始，其实跟时钟类似。

类似时钟机制，假如现在是6点，顺时针加12个小时，这样就回到了6点。

3、先思考，为什么不能直接用源码计算

计算机里没有减法，减一个数，相当于加一个数后得到想要的值，然后就在这条路上去探索了。
1 + （-1） 直接用原码计算是有问题的，还有符号位，所以直接一加是个负数，那这就有问题了。
所以科学家开始想解决办法了

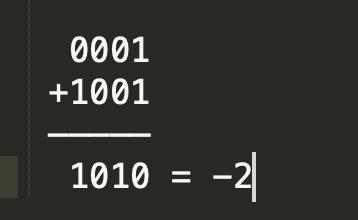
4、主角的由来

由前面可知，数值加上模后会回到原来的位置。

由此将i-j + 模的值等同于 i - j ,   i-j=(i-j)+(2^n-1+1)=i+(2^n-1-j+1)

2^n-1-j ,结果如下图，

这个东西刚好是-1，除符号位外的取反。称为反码

2^n-1-j+1，补码，反码加1 

所以-1最终的补码与1相加 ，得到正确的值

5、反应肯定是？？？

这里的计算算的刚好，这里我看其他人也有相同的迷惑。

问题一：为什么i-j得加上取模的除数？
其实这个换个思路理解就行了，i-j是一个值，这个值加上模，其实就还是会回到原来的位置。

问题二：
最迷糊的地方来了，2^n-1就是32位1，这个地方就又没有符号位这个说吗吗？

作者的解答是：我们只考虑(n-1)位的1，不考虑第一位

一开始其实我也是没太明白这里的解释。
其实就是回去最原始的地方，我们设定为4位，符号位为第四位，最大值也就2^3-1，现在是2^4，如果是真的符号位 也只是第5位作为符号位。

现在想必大家都理解了。如果强制加上符号位，那么和j的值是对应不上长度的。所以把第一位去除直接计算。

这个公式刚好就这么巧解释了整个补码的由来。