盘点面试中常见的超大规模数据常见的算法问题

Posted 2022-12-06 纵横千里，捭阖四方

在大部分算法题目中，默认给定的数据量都很小的，例如只有几个或者十几个元素，但是如果将数据量提高到百万甚至十几亿，那处理逻辑就会发生很大差异，这也是算法考查中，经常出现的一类问题。此时普通的数组、链表、Hash、树等等结构有无效了 ，因为内存空间放不下了。而常规的递归、排序，回溯、贪心和动态规划等思想也无效了，因为执行都会超时，必须另外想办法。这类问题该如何下手呢？这里介绍三种非常典型的思路：

1.使用位存储，使用位存储最大的好处是占用的空间是简单存整数的1/8。例如一个40亿的整数数组，如果用整数存储需要16GB左右的空间，而如果使用位存储，就可以用2GB的空间，这样很多问题就能够解决了。具体方法和原理请参考1.1、1.2和1.5小节。

2.如果文件实在太大 ，无法在内存中放下，则需要考虑将大文件分成若干小块，先处理每个块，最后再逐步得到想要的结果，这种方式也叫做外部排序。这样需要遍历全部序列至少两次，是典型的用时间换空间的方法，详细请看题目1.2中的进阶问题、1.3、1.4和1.5小节。

3.堆，如果在超大数据中找第K大、第K小，K个最大、K个最小，则特别适合使用堆来做。而且将超大数据换成流数据也可以，而且几乎是唯一的方式，口诀就是“查小用大堆，查大用小堆”，详细请看第1.8小节。

1.经典案例

1.1. 用4KB内存寻找重复元素

题目要求：给定一个数组，包含从1到N的整数，N最大为32000，数组可能还有重复值，且N的取值不定，若只有4KB的内存可用，该如何打印数组中所有重复元素。

分析：本身是一道海量数据问题的热身题，如果去掉“只有4KB”的要求，我们可以先创建一个大小为N的数组，然后将这些数据放进来，但是这里数组最大为32KB，而题目有4KB的内存限制，我们就必须先确定该如何存放这个数组。

如果只有4KB的空间，那么只能寻址8*4*2^10个比特，这个值比32000要大的，因此我们可以创建32000比特的位向量(比特数组)，其中一个比特位置就代表一个整数。

利用这个位向量，就可以遍历访问整个数组。如果发现数组元素是v，那么就将位置为v的设置为1，碰到重复元素，就输出一下。

这个做法请认真揣摩清楚，下面的很多题都是这个思想

public class FindDuplicatesIn32000 
    public void checkDuplicates(int[] array) 
        BitSet bs = new BitSet(320000);
        for (int i = 0; i < array.length; i++) 
            int num = array[i];
            int num0 = num - 1;
            if (bs.get(num0)) 
                System.out.println(num);
             else 
                bs.set(num0);
            
        
    
    class BitSet 
        int[] bitset;
​
        public BitSet(int size) 
            this.bitset = new int[size >> 5];
        
​
        boolean get(int pos) 
            int wordNumber = (pos >> 5);//除以32
            int bitNumber = (pos & 0x1F);//除以32
            return (bitset[wordNumber] & (1 << bitNumber)) != 0;
        
​
        void set(int pos) 
            int wordNumber = (pos >> 5);//除以32
            int bitNumber = (pos & 0x1F);//除以32
            bitset[wordNumber] |= 1 << bitNumber;
        
    

1.2.从40个亿中产生一个不存在的整数

题目要求：给定一个输入文件，包含40亿个非负整数，请设计一个算法，产生一个不存在该文件中的整数，假设你有1GB的内存来完成这项任务。

• 进阶：如果只有10MB的内存可用，该怎么办？

本题不用写代码，如果能将方法说清楚就很好了 ，我们接下来一步步分析该如何做。

1.2.1 位图存储大数据的原理

假设用哈希表来保存出现过的数，如果 40 亿个数都不同，则哈希表的记录数为 40 亿条，存一个 32 位整数需要 4B，所以最差情况下需要 40 亿*4B=160 亿字节，大约需要16GB 的空间，这是不符合要求的。

如果数据量很大，采用位方式（俗称位图）存储数据是常用的思路，那位图如何存储元素的呢？ 我们可以使用 bit map 的方式来表示数出现的情况。具体地说， 是申请一个长度为 4 294 967 295 的 bit 类型的数组 bitArr（就是boolean类型），bitArr 上的每个位置只可以表示 0 或1 状态。8 个bit 为 1B，所以长度为 4 294 967 295 的 bit 类型的数组占用 500MB 空间，这就满足题目给定的要求了。

那怎么使用这个 bitArr 数组呢？就是遍历这 40 亿个无符号数，遇到所有的数时，就把 bitArr 相应位置的值设置为 1。例如，遇到 1000，就把bitArr[7000]设置为 1。

遍历完成后，再依次遍历 bitArr，看看哪个位置上的值没被设置为 1，这个数就不在 40 亿个数中。例如，发现 bitArr[8001]==0，那么 8001 就是没出现过的数，遍历完 bitArr 之后，所有没出现的数就都找出来了。

位存储的核心是：我们存储的并不是这40亿个数据本身，而是其对应的位置。这一点明白的话，整个问题就迎刃而解了。

1.2.2 使用10MB来存储

如果现在只有 10MB 的内存，此时位图也不能搞定了，我们要另寻他法。这里我们使用分块思想，时间换空间，通过两次遍历来搞定。

如果只有10MB，我们只要求找到其中一个没出现过的数即可。

首先，将0~4 294 967 295(2^32) 这个范围是可以平均分成 64 个区间的，每个区间是 67 108 864 个数，例如：

• 第0 区间（0~67 108 863）

• 第 1 区间（67 108 864~134 217 728）

• 第 i 区间（67 108 864´I~67 108 864´(i+1)-1），

• ……，

• 第 63 区间（4 227 858 432~4 294 967 295）。

因为一共只有 40 亿个数，所以，如果统计落在每一个区间上的数有多少，肯定有至少一个区间上的计数少于67 108 864。利用这一点可以找出其中一个没出现过的数。具体过程是通过两次遍历来搞定：

第一次遍历，先申请长度为 64 的整型数组 countArr[0..63]，countArr[i]用来统计区间 i 上的数有多少。遍历 40 亿个数，根据当前数是多少来决定哪一个区间上的计数增加。例如，如果当前数是 3 422 552 090 ， 3 422 552 090/67 108 864=51 ， 所以第 51 区间上的计数增加countArr[51]++。遍历完 40 亿个数之后，遍历 countArr，必然会有某一个位置上的值（countArr[i]） 小于 67 108 864，表示第 i 区间上至少有一个数没出现过。我们肯定会找到至少一个这样的区间。

此时使用的内存就是countArr 的大小（64*4B），是非常小的。

假设找到第 37 区间上的计数小于 67 108 864，那么我们对这40亿个数据进行第二次遍历：

1. 申请长度为 67 108 864 的 bit map，这占用大约 8MB 的空间，记为 bitArr[0..67108863]。

2. 遍历这 40 亿个数，此时的遍历只关注落在第 37 区间上的数，记为 num（num满足num/67 108 864==37），其他区间的数全部忽略。

3. 如果步骤 2 的 num 在第 37 区间上，将 bitArr[num - 67108864*37]的值设置为 1，也就是只做第 37 区间上的数的 bitArr 映射。

4. 遍历完 40 亿个数之后，在 bitArr 上必然存在没被设置成 1 的位置，假设第 i 个位置上的值没设置成 1，那么 67 108 864´37+i 这个数就是一个没出现过的数。

总结一下进阶的解法：

1. 根据 10MB 的内存限制，确定统计区间的大小，就是第二次遍历时的 bitArr 大小。

2. 利用区间计数的方式，找到那个计数不足的区间，这个区间上肯定有没出现的数。

3. 对这个区间上的数做 bit map 映射，再遍历bit map，找到一个没出现的数即可。

1.2.3 如何确定分块的区间

在上面的例子中，我们看到采用两次遍历，第一次将数据分成64块刚好解决问题。那我们为什么不是128块、32块、16块或者其他类型呢？

这里主要是要保证第二次遍历时每个块都能放进这10MB的空间中。2^23<10MB<2^24,而2^23=8388608大约为8MB，也就说我们一次的分块大小只能为8MB左右。在上面我们也看到了，第二次遍历时如果分为64块，刚好满足要求。

所以在这里我们最少要分成64块，当然如果分成128块、256块等也是可以的。

1.3. 用 2GB 内存在 20 亿个整数中找到出现次数最多的数

题目要求：有一个包含 20 亿个全是 32 位整数的大文件，在其中找到出现次数最多的数。

要求，内存限制为 2GB。

想要在很多整数中找到出现次数最多的数，通常的做法是使用哈希表对出现的每一个数做词频统计，哈希表的 key 是某一个整数，value 是这个数出现的次数。就本题来说，一共有 20 亿个数，哪怕只是一个数出现了 20 亿次，用 32 位的整数也可以表示其出现的次数而不会产生溢出，所以哈希表的 key 需要占用 4B，value 也是 4B。那么哈希表的一条记录（key,value）需要占用 8B，当哈希表记录数为 2 亿个时，需要至少 1.6GB 的内存。

如果 20 亿个数中不同的数超过 2 亿种，最极端的情况是 20 亿个数都不同，那么在哈希表中可能需要产生 20 亿条记录，这样内存会不够用，所以一次性用哈希表统计 20 亿个数的办法是有很大风险的。

解决办法是把包含 20 亿个数的大文件用哈希函数分成 16 个小文件，根据哈希函数的性质，同一种数不可能被散列到不同的小文件上，同时每个小文件中不同的数一定不会大于 2 亿种， 假设哈希函数足够优秀。然后对每一个小文件用哈希表来统计其中每种数出现的次数，这样我们就得到了 16 个小文件中各自出现次数最多的数，还有各自的次数统计。接下来只要选出这16 个小文件各自的第一名中谁出现的次数最多即可。

把一个大的集合通过哈希函数分配到多台机器中，或者分配到多个文件里，这种技巧是处理大数据面试题时最常用的技巧之一。但是到底分配到多少台机器、分配到多少个文件，在解题时一定要确定下来。可能是在与面试官沟通的过程中由面试官指定，也可能是根据具体的限制来确定，比如本题确定分成 16 个文件，就是根据内存限制 2GB 的条件来确定的。

1.4.从100 亿个 URL中查找的问题

题目：有一个包含 100 亿个 URL 的大文件，假设每个 URL 占用 64B，请找出其中所有重复的 URL。补充问题：某搜索公司一天的用户搜索词汇是海量的（百亿数据量），请设计一种求出每天热门 Top 100 词汇的可行办法。

解答：原问题的解法使用解决大数据问题的一种常规方法：把大文件通过哈希函数分配到机器， 或者通过哈希函数把大文件拆成小文件，一直进行这种划分，直到划分的结果满足资源限制的要求。首先，你要向面试官询问在资源上的限制有哪些，包括内存、计算时间等要求。在明确了限制要求之后，可以将每条 URL 通过哈希函数分配到若干台机器或者拆分成若干个小文件， 这里的“若干”由具体的资源限制来计算出精确的数量。

例如，将 100 亿字节的大文件通过哈希函数分配到 100 台机器上，然后每一台机器分别统计分给自己的 URL 中是否有重复的 URL，同时哈希函数的性质决定了同一条 URL 不可能分给不同的机器；或者在单机上将大文件通过哈希函数拆成 1000 个小文件，对每一个小文件再利用哈希表遍历，找出重复的 URL；还可以在分给机器或拆完文件之后进行排序，排序过后再看是否有重复的 URL 出现。总之，牢记一点，很多大数据问题都离不开分流，要么是用哈希函数把大文件的内容分配给不同的机器，要么是用哈希函数把大文件拆成小文件，然后处理每一个小数量的集合。

补充问题最开始还是用哈希分流的思路来处理，把包含百亿数据量的词汇文件分流到不同的机器上，具体多少台机器由面试官规定或者由更多的限制来决定。对每一台机器来说，如果分到的数据量依然很大，比如，内存不够或存在其他问题，可以再用哈希函数把每台机器的分流文件拆成更小的文件处理。处理每一个小文件的时候，通过哈希表统计每种词及其词频，哈希表记录建立完成后，再遍历哈希表，遍历哈希表的过程中使用大小为 100 的小根堆来选出每一个小文件的 Top 100（整体未排序的 Top 100）。每一个小文件都有自己词频的小根堆（整体未排序的 Top 100），将小根堆里的词按照词频排序，就得到了每个小文件的排序后 Top 100。然后把各个小文件排序后的 Top 100 进行外排序或者继续利用小根堆，就可以选出每台机器上的 Top100。不同机器之间的 Top 100 再进行外排序或者继续利用小根堆，最终求出整个百亿数据量中的 Top 100。对于 Top K 的问题，除用哈希函数分流和用哈希表做词频统计之外，还经常用堆结构和外排序的手段进行处理。

1.5. 40 亿个非负整数中找到出现两次的数和所有数的中位数

题目要求：32 位无符号整数的范围是 0～4 294 967 295，现在有 40 亿个无符号整数，可以使用最多 1GB的内存，找出所有出现了两次的数。

进阶：可以使用最多 10MB 的内存，怎么找到这 40 亿个整数的中位数？

本题可以看做第一题的进阶问题，这里将出现次数限制在了两次。

首先，可以用 bit map 的方式来表示数出现的情况。具体地说，是申请一个长度为4 294 967 295x2 的bit 类型的数组bitArr，用 2 个位置表示一个数出现的词频，1B 占用 8 个bit， 所以长度为 4 294 967 295x2 的 bit 类型的数组占用 1GB 空间。怎么使用这个 bitArr 数组呢？遍历这 40 亿个无符号数，如果初次遇到 num，就把bitArr[num*2 + 1]和 bitArr[num*2]设置为 01， 如果第二次遇到 num，就把bitArr[num*2+1]和bitArr[num*2]设置为 10，如果第三次遇到 num， 就把bitArr[num*2+1]和bitArr[num*2]设置为 11。以后再遇到 num，发现此时 bitArr[num*2+1]和 bitArr[num*2]已经被设置为 11，就不再做任何设置。遍历完成后，再依次遍历 bitArr，如果发现bitArr[i*2+1]和bitArr[i*2]设置为 10，那么 i 就是出现了两次的数。

对于进阶问题，用分区间的方式处理，长度为 2MB 的无符号整型数组占用的空间为 8MB， 所以将区间的数量定为 4 294 967 295/2M，向上取整为 2148 个区间。第 0 区间为0~2*M*-1，第 1 区间为 2*M*~4*M*-1，第 i 区间为2M*j!~2M*(i+1)-1……

申请一个长度为 2148 的无符号整型数组 arr[0..2147]，arr[i]表示第 i 区间有多少个数。arr必然小于 10MB。然后遍历 40 亿个数，如果遍历到当前数为 num，先看 num 落在哪个区间上（num/2M），然后将对应的进行 arr[num/2M]++操作。这样遍历下来，就得到了每一个区间的数的出现状况，通过累加每个区间的出现次数，就可以找到 40 亿个数的中位数（也就是第 20 亿个数）到底落在哪个区间上。比如，0~*K*-1区间上数的个数为 19.998 亿，但是发现当加上第 K 个区间上数的个数之后就超过了 20 亿，那么可以知道第 20 亿个数是第 K 区间上的数，并且可以知道第 20 亿个数是第 K 区间上的第 0.002 亿个数。

接下来申请一个长度为 2MB 的无符号整型数组countArr[0..2M-1]，占用空间 8MB。然后遍历 40 亿个数，此时只关心处在第 K 区间的数记为numi ，其他的数省略， 然后将countArr[numi-K*2M]++，也就是只对第 K 区间的数做频率统计。这次遍历完 40 亿个数之后，就得到了第 K 区间的词频统计结果countArr，最后只在第 K 区间上找到第 0.002 亿个数即可。

1.6. 对20GB文件进行排序

题目要求：假设你有一个20GB的文件，每行一个字符串，请说明如何对这个文件进行排序？

分析：这里给出大小是20GB，其实面试官就在暗示你不要将所有的文件都装入到内存里，因此我们只能将文件划分成一些块，每块大小是xMB，x就是可用内存的大小，例如1GB一块，那我们就可以将文件分为20块。我们先对每块进行排序，然后再逐步合并。这时候我们可以使用两两归并，也可以使用堆排序策略将其逐步合并成一个。相关方法我们在《查找》一章的堆排部分有介绍。

这种排序方式也称为外部排序。

1.7. 超大文本中搜索两个单词的最短距离

题目要求：有个超大文本文件，内部是很多单词组成的，现在给定两个单词，请你找出这两个单词在这个文件中的最小距离，也就是像个几个单词。你有办法在O(1)时间里完成搜索操作吗？方法的空间复杂度如何。

分析：这个题咋看很简单，遍历一下，找到这两个单词w1和w2的位置然后比较一下就可以了，然而这里的w1可能在很多位置出现，而w2也会在很多位置出现，如下图：

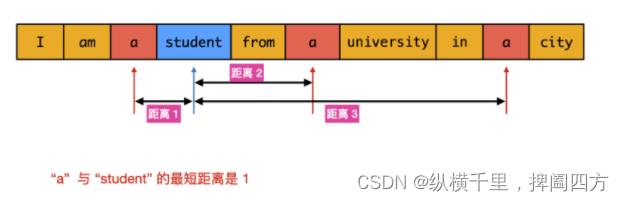
 这时候如何比较寻找哪两个是最小距离呢？

最直观的做法是遍历数组 words，对于数组中的每个word1，遍历数组words 找到每个word2并计算距离。该做法在最坏情况下的时间复杂度是 O(n^2)，需要优化。

本题我们少不了遍历一次数组，找到所有word1 和word2出现的位置，但是为了方便比较，我们可以将其放到一个数组里，例如：

listA:1,2,9,15,25
listB:4,10,19
合并成
list:1a,2a,4b,9a,10b,15a,19b,25a

合并成一个之后更方便查找，数字表示出现的位置，后面一个元素表示元素是什么。然后一边遍历一边比较就可以了。

但是对于超大文本，如果文本太大那这个list可能溢出。如果继续观察，我们会发现其实不用单独构造list，从左到右遍历数组 \\textitwordswords，当遍历到 word1时，如果已经遍历的单词中存在word2 ，为了计算最短距离，应该取最后一个已经遍历到的 word2所在的下标，计算和当前下标的距离。同理，当遍历到word2时，应该取最后一个已经遍历到的word1所在的下标，计算和当前下标的距离。

基于上述分析，可以遍历数组一次得到最短距离，将时间复杂度降低到O(n)。用index1和index2分别表示数组words 已经遍历的单词中的最后一个word1的下标和最后一个word2的下标，初始时index1 =index2=−1。遍历数组words，当遇到word2时，执行如下操作：

• 如果遇到word1 ，则将index1更新为当前下标；如果遇到word2，则将index2更新为当前下标。

• 如果index1和index2都非负，则计算两个下标的距离 ∣index1−index2 ∣，并用该距离更新最短距离。

遍历结束之后即可得到word1和word2的最短距离。

python：

class Solution:
    def findClosest(self, words: List[str], word1: str, word2: str) -> int:
        ans = len(words)
        index1, index2 = -1, -1
        for i, word in enumerate(words):
            if word == word1:
                index1 = i
            elif word == word2:
                index2 = i
            if index1 >= 0 and index2 >= 0:
                ans = min(ans, abs(index1 - index2))
        return ans


java：

class Solution 
    public int findClosest(String[] words, String word1, String word2) 
        int length = words.length;
        int ans = length;
        int index1 = -1, index2 = -1;
        for (int i = 0; i < length; i++) 
            String word = words[i];
            if (word.equals(word1)) 
                index1 = i;
             else if (word.equals(word2)) 
                index2 = i;
            
            if (index1 >= 0 && index2 >= 0) 
                ans = Math.min(ans, Math.abs(index1 - index2));
            
        
        return ans;
    

时间复杂度：O(n)，其中 nn 是数组words 的长度。需要遍历数组一次计算 word1和word2的最短距离，每次更新下标和更新最短距离的时间都是 O(1)。这里将字符串的长度视为常数。

空间复杂度：O(1)。

进阶问题 如果寻找过程在这个文件中会重复多次，而每次寻找的单词不同，则可以维护一个哈希表记录每个单词的下标列表。遍历一次文件，按照下标递增顺序得到每个单词在文件中出现的所有下标。在寻找单词时，只要得到两个单词的下标列表，使用双指针遍历两个下标链表，即可得到两个单词的最短距离。

1.8. 从10亿数字中寻找最小的100万个数字

题目要求：设计一个算法，给定一个10亿个数字，找出最小的100万的数字。假定计算机内存足以容纳全部10亿个数字。

分析：

本题有三种常用的方法，一种是先排序所有元素，然后取出前100万个树 ，该方法的时间复杂度为O(nlogn)。很明显对于10亿级别的数据，这么做时间和空间代价太高。

第二种方式是采用选择排序的方式，首先遍历10亿个数字找最小，然后再遍历一次找第二小 ，然后再一次找第三小，直到找到第100万个。很明显这种方式的时间代价是O(nm)也就是要执行10亿*100万次，这个效率一般的服务器都达不到。

第三种方式，采用大顶堆来解决，堆的原理在《查找》一章专门介绍过，方法思想是一致的，都是“查小用大堆，查大用小堆”。

首先，为前100万个数字创建一个大顶堆，最大元素位于堆顶。

然后，遍历整个序列，只有比堆顶元素小的才允许插入堆中，并删除原堆的最大元素。

之后继续遍历剩下的数字，最后剩下的就是最小的100万个。

采用这种方式，只需要遍历一次10亿个数字，还可以接受。更新堆的代价是O(nlogn),也勉强能够接受。堆占用的空间是100万*4，大约为4MB左右的空间就够了，因此也能接收。

如果数据量没有这么大，也是可以直接使用这三种方式的。

如果将10亿数字换成流数据，也可以使用堆来找，而且对于流数据，几乎只能用堆来做。