字典树原理与实现

Posted 2022-12-06 白龙码~

文章目录

• 字典树
• • 一、字典树节点
  • 二、字典树的插入
  • 三、字典树的查询
  • 四、算法练习
  • • [LeetCode 2416. 字符串的前缀分数和](https://leetcode.cn/problems/sum-of-prefix-scores-of-strings/)

字典树

字典树(trie)，又称前缀树，或单词查找树，是一棵专用于查找单词或单词前缀是否存在的树。

一、字典树节点

字典树的节点一般包含一个字典树节点指针数组，用来存储它的孩子。

class Trie

    vector<Trie*> ch;

当所有单词都由小写字母构成时，数组的大小为26，即26个小写字母。

---

二、字典树的插入

以插入单词an为例：

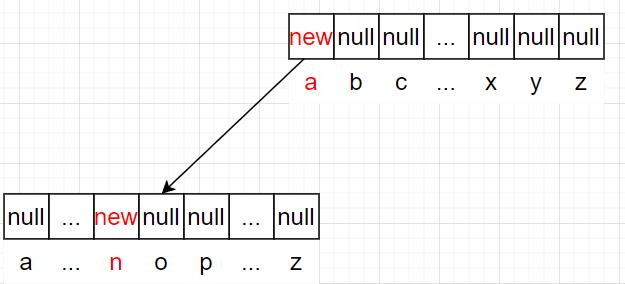
第一个字母为a，所以在根节点处为a创建一个孩子节点，将孩子节点的地址填入ch数组下标为'a'-'a'处。此时我们递归至新创建的孩子节点，处理下一个字母。

第二个字母为n，所以为n创建一个孩子节点，并将孩子节点的地址填入ch数组下标为'n'-'a'处。

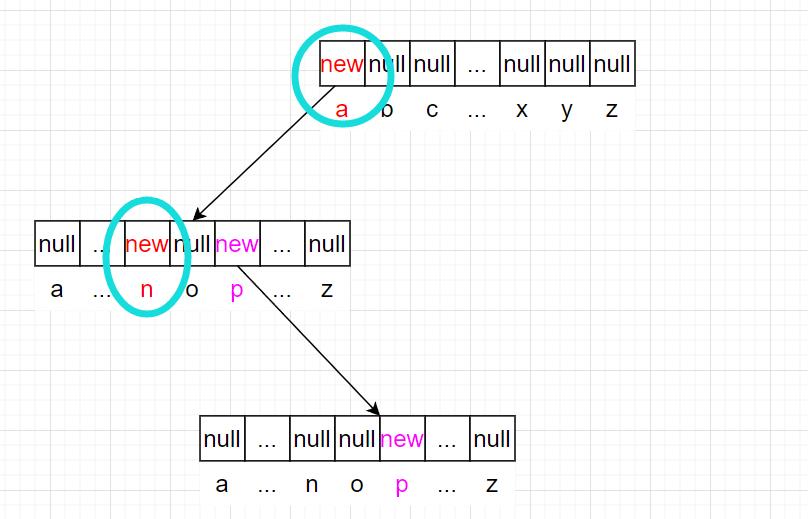
如果再插入app呢：

根节点处a的孩子节点已经创建，因此递归至第二层。

第二层p的孩子节点为空，因此new一个，递归至第三层。

第三层p孩子节点为空，因此new一个，递归结束。

总结：

插入操作是一种递归式的，第一个字母对应根节点，第二个字母对应第一个字母对应位置的孩子节点。

但是，一般为了效率，使用非递归的方式进行插入。

void insert(const string& s)

    int n = s.size();
    Trie* trie = this; // 当前所在的字典树节点
    for (int i = 0; i < n; ++i)
    
        if (trie->dic[s[i] - 'a'] == nullptr)
            trie->dic[s[i] - 'a'] = new Trie;
        trie = trie->dic[s[i] - 'a'];
    

---

三、字典树的查询

与插入类似，插入在对应位置为空时，创建一个新结点，而查询在对应位置为空时，表明不存在对应的单词或前缀。

比如，在上述字典树的基础上查询an时，从根节点递归下来，没有空节点，说明an是存在的。

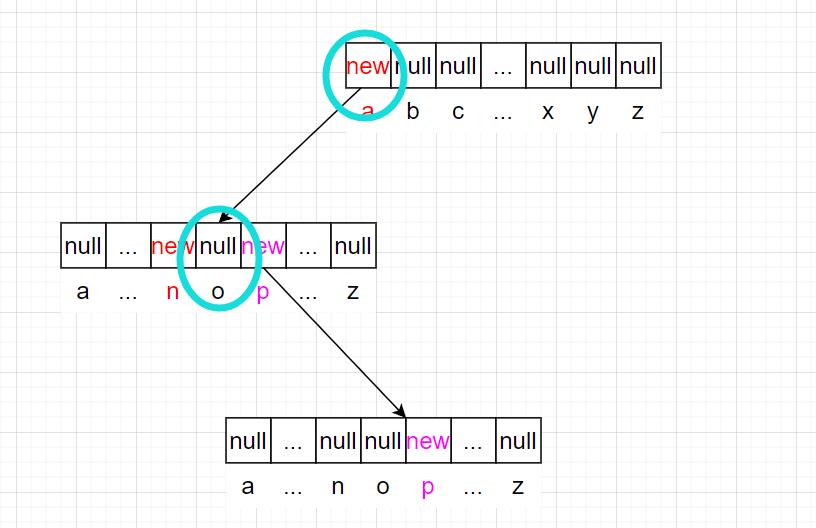
而查询ao时，在第二层发现o为空，因此判定：ao不存在。

bool query(const string& s)

    int n = s.size();
    Trie* trie = this; // 当前所在的字典树节点
    for (int i = 0; i < n; ++i)
    
        if (trie->cnt[s[i] - 'a'] == nullptr)
            return false;
        trie = trie->dic[s[i] - 'a'];
    
    return true;

---

四、算法练习

LeetCode 2416. 字符串的前缀分数和

class Trie

    vector<Trie*> dic;
    vector<int> cnt; // 记录以c为最后一个字符的前缀有多少个
public:
    Trie()
    
        dic.resize(26, nullptr);
        cnt.resize(26, 0);
    
    void add(const string& s)
    
        int n = s.size();
        Trie* trie = this;
        for (int i = 0; i < n; ++i)
        
            if (trie->dic[s[i] - 'a'] == nullptr)
                trie->dic[s[i] - 'a'] = new Trie;
            trie->cnt[s[i] - 'a']++;
            trie = trie->dic[s[i] - 'a'];
        
    
    int query(const string& s)
    
        int n = s.size();
        Trie* trie = this;
        int res = 0;
        for (int i = 0; i < n; ++i)
        
            res += trie->cnt[s[i] - 'a'];
            trie = trie->dic[s[i] - 'a'];
        
        return res;
    
;
class Solution 

    Trie trie;
public:
    vector<int> sumPrefixScores(vector<string>& words) 
    
        for (auto& word : words)
        
            trie.add(word);
        
        vector<int> res;
        for (auto& word : words)
        
            res.emplace_back(trie.query(word));
        
        return res;
    
;