拐点检测常用算法介绍

Posted 2022-12-06 Wallace JW

前言

最近在学习拐点检测的相关问题， 发现 C.Truong 的论文 对拐点检测的整个流程和目前主流的一些算法介绍的比较清楚，所以在这里进行了一些记录以及总结，并且对 Truong 发布的 ruptures 库做了一些简单的介绍。如果想要进行更深入的研究，请参考原论文和 ruptures。

文章目录

• 前言
• 概览
• • 问题定义
  • 符号定义
  • 研究方法
• 损失函数
• • Piecewise i.i.d. signals
  • • 例一：Mean-shifts for normal data
    • 例二：Mean-shifts and scale-shifts for normal data
    • 例三：Count data
  • Linear model
  • • 例四：Autoregressive model
  • Kernel change point detection
  • Mahalanobis-type metric
  • 损失函数总结
• 应用于固定 K 的查找算法
• • 最优检测 Optimal Detection
  • • 简介
    • 伪代码
  • 滑动窗口 Window sliding
  • • 简介
    • 伪代码
  • 二分分割 Binary segmentation
  • • 简介
    • 伪代码
  • 自底向上分割 Bottom-up segmentation
  • • 简介
    • 伪代码
• 应用于可变 K 值的查找算法
• • $l_0$ 惩罚项 （$l_0$ penalty）
  • • 简介
    • Pelt 算法
    • 伪代码
  • $l_1$ 惩罚项 （ $l_1$ penalty）
  • 其他惩罚项
• 贝叶斯方法
• ruptures 库简介
• 总结

概览

问题定义

拐点检测名为 change point detection，对于一条不平缓的时间序列曲线，认为存在一些时间点 $(t_1,t_2,...,t_k)$，使得曲线在这些点对应的位置发生突变，这些时间点对应的曲线点称为拐点，在连续的两个拐点之间，曲线是平稳的。

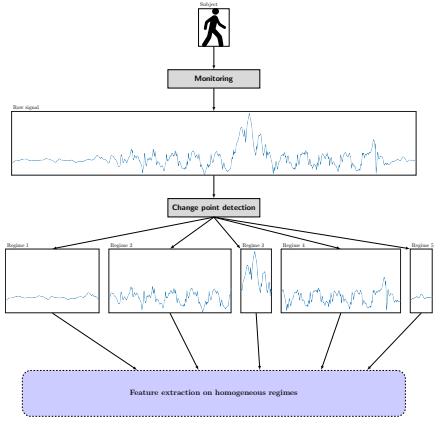
拐点检测算法的质量通过算法输出拐点与实际观测到的拐点的差值绝对值除以样本数来评估。
$$\forall k,\left|{\hat{t}}_k-t_k^{\star }\right|/T,$$
理想情况下，当样本数T无穷大时，误差应该减少到0，这种性质称为满足渐近一致性 (asymptotic consistency.)
$$\underset{k=1,\dots ,K^{\ast }}{\max }\left|{\hat{t}}_k-t_k^{\star }\right|/T\stackrel{p}{⟶}0$$

符号定义

$y_{a..b}$ 表示时间点 a 和 b 之间的时间序列，因此完整信号为 $y_{0..T}$。

对于给定的拐点索引 $t$，它的关联分数 associate fraction 称为拐点分数 change point fractions ，公式为 ：
$$\tau :=t/T\in (0,1].$$

拐点分数的集合 $\mathbf{\tau }={\tau }_1,{\tau }_2,\dots$ 写作 $|\mathbf{\tau }$|

研究方法

一般思路是构造一个对照函数 contrast function，目标是将对照函数的值最小化。
$$V(\mathbf{t},y):=\sum _{k=0}^{K}c\left(y_{t_k\dots t_{k+1}}\right)，$$
其中 $c(\cdot )$ 表示用来测量拟合度 goodness-of-fit 的损失函数 cost function, 损失函数的值在均匀的子序列上较低，在不均匀的子序列上较高。

基于离散优化问题 discrete optimization problem，拐点的总数量记为 $K$ ：

如果 $K$ 是固定值，估算的拐点值为：
$${\min }_{|\mathbf{t}|=K}V(\mathbf{t}),$$
如果 $K$ 不是固定值，估算的拐点值为：
$$\underset{t}{\min }V(\mathbf{t})+\mathrm{pen}(\mathbf{t}).$$
其中 $pen(t)$为对 $t$ 的惩罚项项

在这种方法论下，拐点检测的算法包含以下三个元素：

1. 选择合适的损失函数来测算子序列的均匀程度 homogeneity，这与要检测的变化类型有关
2. 解决离散优化问题
3. 合理约束拐点的数量，确定使用固定的 $K$ 还是用 $pen()$ 来惩罚 penalizing 不固定的数量

损失函数

损失函数与被检测拐点的变化类型有关，下文介绍的损失函数使用在子序列 $y_{a..b}$ 上，其中 $1<=a<b<=T$

Piecewise i.i.d. signals

首先介绍一种使用 $i.i.d.$ 变量对信号 $y$ 进行建模的一般参数模型。

$i.i.d.$ Independent and identically distributed，独立同分布，指一组随机变量中每个变量的概率分布都相同，且这些随机变量互相独立。

假设 $y_1,...,y_T$ 是独立随机变量，概率分布 probability distribution $f\left(y_t|\theta \right)$ 依赖于向量值参数 $\theta$ vector-value parameter，$\theta$ 表示预测到发生突然变化的兴趣点。假设存在一系列真实的拐点 ${\mathrm{t}}^{\star }=t_1^{\star },\dots$，并且满足：
$$y_t\sim \sum _{i=0}^{K}f\left(\cdot |{\theta }_k\right),(t_k^{\star }$$

计算机视觉逼近拐点，微软算法正跨越“一步之遥”

根据线拐点的表格坐标信息批量生成奥维地图轨迹

图像边缘提取简介

拐点怎么求 计算方法是啥

华为张顺茂：迎接拐点，拥抱计算新架构

曲线非线性转折点怎么求