[机器学习] UFLDL笔记 - PCA and Whitening

Posted 2022-12-06 WangBo_NLPR

前言　　

　　[机器学习] UFLDL笔记系列是以我学习UFLDL Tutorial（Andrew Ng老师主讲）时的笔记资料加以整理推出的。内容以无监督特征学习和深度学习为主，同时也参考了大量网上的相关资料。
　　
　　撰写本文的原因是最近项目中用到了“度量学习（Metric Learning）”，其中在特征预处理部分用到了“PCA-Whitening”，而PCA-Whitening是以PCA为基础的。作为对这项工作的总结的一部分，也作为对UFLDL中PCA学习笔记的整理，于是撰写本文。
　　
　　本文的理论部分主要整理自UFLDL的“PCA”章节和一些经典教材，同时也参考了网上的一些经典博客，包含了PCA和Whitening的一些基本概念、推导和代码实现，供读者参考。同时本文也结合了实际项目中遇到的问题对PCA-Whitening的应用进行了讨论。
　　
　　文章小节安排如下：
　　1）PCA的基本原理
　　2）数据降维（Reducing the Data Dimension）
　　3）PCA的性质及缺点
　　4）PCA-Whitening
　　5）ZCA-Whitening
　　

一、PCA的基本原理　　

1.1 基本概念

　　PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。
　　在我的项目经验中，利用PCA主要做两个事情：
　　
　　1）高维特征的降维，以提高运算速度，虽然这个年代计算能力发展迅猛，但在一些工作中降维还是很有必要的预处理操作；
　　2）PCA-Whitening对特征预处理，以去除特征之间的相关性，这是很多算法的预处理步骤，比如我最近在做的JointBayesian算法；
　　
　　

1.2 什么是特征向量

　　首先要知道数据的变化是有方向的，而且变化方向有主次之分（有多少个维度就有多少个变化方向），代表数据变化的方向向量就是特征向量。
　　看图示：
　　

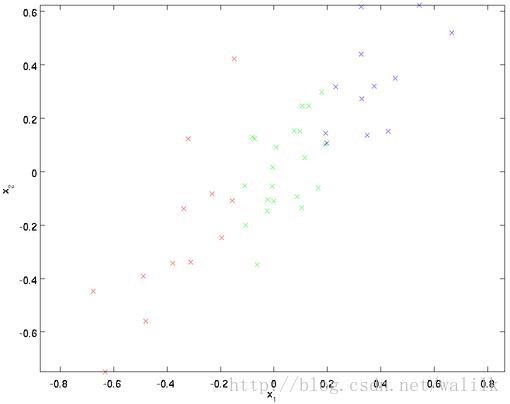
　　在这个二维平面中，可以明显看出，u ₁ 是数据变化的主方向，而 u ₂ 是次方向。如下。
　　
　　
　　

1.3 求解特征向量

　　首先计算出矩阵 ∑ ，如下所示：
　　

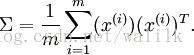
　　 假设 x 的均值为零，那么 ∑ 就是 x 的协方差矩阵（covariance matrix）。
　　如上特征是2维的，那么协方差矩阵 ∑ 就是一个2x2的矩阵，其中第一个向量就是上图中的u ₁（主特征向量），第二个向量就是 u ₂（次特征向量）。
　　
　　利用matlab函数或者c++中的一些矩阵运算库（Eigen）可以很容易求得特征向量，当然自己写也不难，只是优化的肯定不如这些库。
　　
　　

Matlab：

　　Sigma = X’ * X / (size(X, 1) - 1);
　　[U, S, V] = svd(Sigma);
　　其中，U就是特征向量矩阵，求解出的特征向量矩阵如下所示：
　　
　　
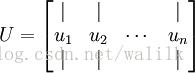
　　此处， u ₁是主特征向量（the principal eigenvector）（对应最大的特征值）， u ₂ 是次特征向量，以此类推。
　　S是特征值向量，记 λ ₁, λ ₂, … , λ _n 为相应的特征值。
　　

1.4 旋转数据（Rotating the Data）

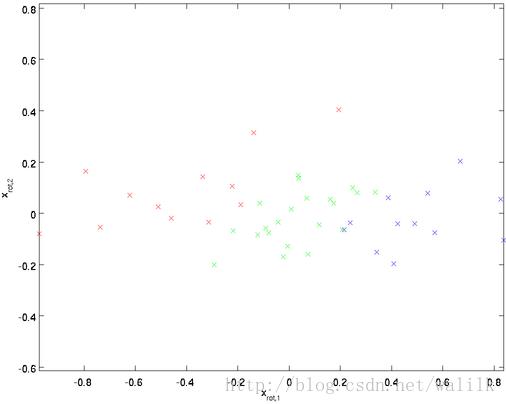
　　接着上面的例子，
　　

　　如图中所示，数据的变化方向并没有与坐标轴对应上，说明数据之间是存在相关性的，也就是存在一定冗余，我们求解特征向量的目的，就是为了通过一定操作来去除数据的这种相关性。
　　
　　在本例中，u_1和u_2构成了一个新 基（basis），可以用来表示数据，也就是说，我将要利用这组新基来重新表示数据，目的是使得数据的变化方向与坐标轴对应，这样就去除数据之间的相关性了。
　　
　　怎么重新表示呢？ 术语是rotate（旋转），或者说，reflect（映射）。
　　
　　公式：
　　
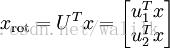
　　观察旋转后的数据分布：
　　
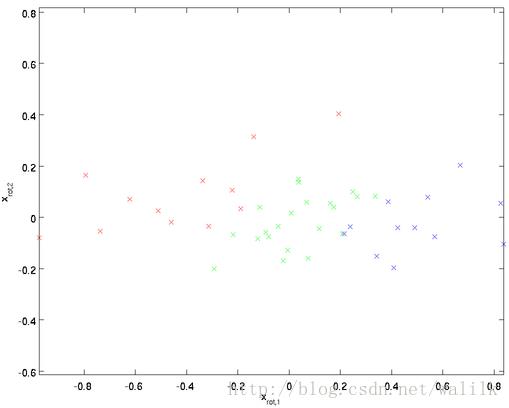
　　这就是把训练数据集旋转到新基 (u ₁, u ₂) 后的结果。
　　
　　阵 U 有正交性（orthogonal），即满足
　　
　　因此若想将旋转后的向量 x _rot 还原为原始数据 x，将其左乘矩阵 U 即可：
　　
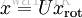
　　验算一下：
　　
　　
　　

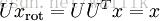
补充：基（basis）

　　 在线性代数中，基（也称为基底）是描述、刻画向量空间的基本工具。 向量空间的基是它的一个特殊的子集，基的元素称为基向量。向量空间中任意一个元素，都可以唯一地表示成基向量的线性组合。如果基中元素个数有限，就称向量空间为有限维向量空间，将元素的个数称作向量空间的维数。
　　定义：
　　一个向量空间，如果存在一个线性无关的向量组x1,…xn,…，使得空间中所有的向量，都能被这个向量组线性表示，那么这个向量组就是这个空间的基。
　　一个基（basis）中的向量是线性无关的，那么这组向量的子集同样是是线性无关的。所以说，从一个基（basis）中任意选取N个向量（N<基的维数），都可以构成一个新的基底（basis）。
　　
　　那么PCA也就可以这样理解：
　　 通过构建低维空间的基，将原始样本特征映射到低维空间中。
　　
　　
　　从几何上解释，一维基底可以是任意的非零向量，二维基底为不共线的2个向量，三维基底为不共面的3个向量，依次类推。
　　从代数上解释，基底即为一组线性无关的向量。一维基底为非零向量，二维基底为含2个向量的线性无关组，三维基底为含3个向量的线性无关组，依次类推。
　　基向量并不唯一，但是通常选取单位向量作为基向量，将基底都化为单位向量的做法称为向量的单位化。
　　
　　

二、数据降维（Reducing the Data Dimension）　

2.1 降维的概念和意义

　　简单来说，将原始的100维的特征数据作为输入，通过算法输出为50维的新特征数据，同时最大限度的保留了原始特征数据的信息。这就是降维操作。
　　降维当然意味着信息的丢失，不过在绝大多数情况下，实际数据是存在着冗余的（即特征项之间有相关性），所以我们可以想办法进行降维，同时还可以最大限度的保留信息（损失尽量降低）。
　　
　　举例来说，
　　举个例子，假如某学籍数据有两列M和F，其中M列的取值是如何此学生为男性取值1，为女性取值0；而F列是学生为女性取值1，男性取值0。此时如果我们统计全部学籍数据，会发现对于任何一条记录来说，当M为1时F必定为0，反之当M为0时F必定为1。在这种情况下，我们将M或F去掉实际上没有任何信息的损失，因为只要保留一列就可以完全还原另一列。（参考：http://blog.codinglabs.org/articles/pca-tutorial.html）
　　
　　
　　关于降维意义，
　　很多人认为在目前机器性能大幅提升的时代，机器学习算法中不需要对特征进行降维操作，但很多机器学习算法的复杂度和数据的维数是密切相关的，甚至与维数呈指数级关系，有经验的同学知道实际任务中处理成千上万甚至几十万维特征的情况并不罕见。此时，过多的特征项会致使很多计算效率低下，甚至不可操作。
　　
　　比如我最近用JointBayesian方法训练度量矩阵，原始2000多维的特征在训练阶段消耗了60多GB的内存（我可怜的服务器也就64GB内存），而且速度非常慢，跑了快5天才出结果（当然服务器CPU也不是特别好）。这样的资源消耗和速度是我无法接受的，原因如下：
　　1：我的目的是实验该特征在度量学习后的效果如何，需要尝试不同参数的组合，可一次实验就要跑5天，验证起来耗时太久；
　　2：我就这么一台服务器还被占满了内存，其他什么实验都跑不了了；
　　3：等是最痛苦的事情。
　　
　　在实验阶段我是希望能够快速验证一些想法，从而及时调整思路，但如果效率这么低，那么idea早就被别人想到拿去发paper了，所以此时一些降维操作非常必要。
　　当然，降维毕竟会损失信息，所以在验证了一些实验想法后，我还是会用原始特征来做最终的实验，通常效果是比较好的。
　　
　　
　　下面总结一下降维的作用和意义：
　　1）避免curse of dimensionality
　　当特征数量p过多，甚至多过数据量N的时候，很可能会产生curse of dimensionality，此时降维是必须的。我们知道越高的维度会使得数据在每个特征维度上的分布越稀疏，这对机器学习算法基本都是灾难性的。过高的特征维度不仅会增加计算的复杂度，也会给后续的分类任务造成负面影响。
　　对于线性模型来说，自相关会让很多模型的效果变差，因此使用的时候先降维再计算会好的多。
　　
　　2）降低模型复杂度
　　特征相互间有相关性在分布上是椭圆的，这会给机器学习模型带来复杂性，会更容易造成模型过拟合。PCA用一组正交基重构特征表达，可以把特征分布拉圆，这就相当于找到了数据的结构性，利用这些先验去简化问题，对模型来说是帮了大忙的。
　　可以试试把一个椭圆分布的样本集直接塞给SVM；再白化后（拉成圆）试试。
　　
　　

2.2 降维的计算

　　继续之前的例子，假如想把数据 x ∈ Rⁿ 降到 k 维表示（x ∈ R^k，令 k 小于n），只需选取 x_rot 的前 k 个成分即可，分别对应前 k 个数据变化的主方向。
　　PCA算法做的其实就是丢弃 x_rot 中后面（取值较小）的成分，就是将这些成分的值近似为零。具体的说，设 x~ 是 x_rot 的近似表示，那么将 x_rot 中除了前 k 个成分外，其余全赋值为零即可，如下：
　　

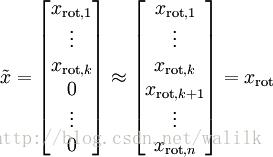
　　在UFLDL的例子中，取 n=2, k=1，可得 x~ 的点图如下：
　　
　　然而，由于上面 x~ 的后 n-k 项均为零，没必要把这些零项保留下来。所以，我们仅用前 k 个（非零, non-zero）成分来定义 k 维向量 x~ 。
　　这也解释了我们为什么会以：
　　
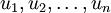
　　为基来表示数据。因为要决定保留哪些成分变得很简单，只需取前 k 个成分即可。这时也可以说，我们“保留了前 k 个 PCA（主）成分”（retaining the top k PCA (or principal) components）。
　　
　　

2.3 数据近似还原（Recovering an Approximation of the Data）

　　根据PCA原理，数据降维其实就是旋转后取k个主成分，那么数据恢复也就容易计算，只需要：
　　

　　进一步，我们把 x~ 看作将 x _rot 的最后 n-k 个元素被置0所得的近似表示，因此如果给定 x~ ∈ R ^k，可以通过在其末尾添加 n-k 个 0 来得到对 x _rot ∈ R ⁿ 的近似，最后，左乘 U 便可近似还原出原数据 x 。具体来说，计算如下：
　　
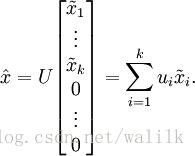
　　上面的等式基于先前对 U 的定义。在实现时，我们实际上并不先给 x~ 填0然后再左乘 U ，因为这意味着大量的乘 0 运算。我们可用 x~ ∈ R ^k 来与 U 的前 k 列相乘，即上式中最右项，来达到同样的目的。将该算法应用于本例中的数据集，可得如下关于重构数据 x~ 的点图：
　　
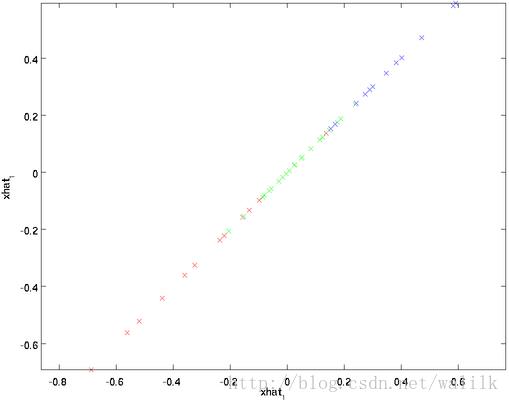
　　由图可见，我们得到的是对原始数据集的一维近似重构。
　　
　　

2.4 主成分选择（Number of components to retain）

　　主成分数量选择也就是k的选择，如果令k=n，那么就只做旋转（rotate），映射到另一个基（basis决定 k 值时，我们通常会考虑不同 k 值可保留的方差百分比。具体来说，如果 k=n ，那么我们得到的是对数据的完美近似，也就是保留了100%的方差，即原始数据的所有变化都被保留下来；相反，如果 k=0 ，那等于是使用零向量来逼近输入数据，也就是只有0%的方差被保留下来。
　　设 λ₁, λ₂, λ₃, … , λ_n表示协方差矩阵 ∑ 的特征值，那么如果保留前 k 个成分，则保留的方差百分比可计算为：
　　

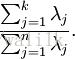
　　那么问题来了，如何选择k？
　　以处理图像数据为例，一个惯常的经验法则是选择 k 以保留99%的方差，换句话说，我们选取满足以下条件的最小 k 值：
　　
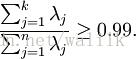
　　对其它应用，如不介意引入稍大的误差，有时也保留90-98%的方差范围。
　　更详细的讲解可以参考UFLDL的相关章节。
　　
　　

2.5 PCA的预处理

　　为使PCA算法正常工作，通常需要满足以下要求：
　　(1) 特征的均值大致为 0；
　　(2) 不同特征的方差值彼此相似。
　　
　　在图像处理领域（假定是自然图像）通常不需要进行方差归一化，因为理论上图像任一部分的统计性质都应该和其它部分相同，这种特性被称作平稳性（stationarity）。因此图像数据天生满足条件(2)。
　　
　　唯一还需进行的规整化操作就是均值规整化/均值归一化（mean normalization），其目的是保证所有特征的均值都在 0 附近。为什么可以这么做？因为在大多数情况下，我们并不关注所输入图像的整体明亮程度（bright）。比如在对象识别任务（object recognition tasks）中，图像的整体明亮程度（brightness）并不会影响图像中存在的是什么物体。更为正式地说，我们对图像块的平均亮度值（mean intensity value）不感兴趣，所以可以减去这个值来进行均值规整化。
　　
　　

三、PCA的性质及缺点　　

3.1 PCA的特点

　　1）PCA算法对输入数据具有缩放不变性
　　PCA算法对输入数据具有缩放不变性，无论输入数据的值被如何放大（或缩小），返回的特征向量都不改变。更正式的说：如果将每个特征向量 x 都乘以某个正数（即所有特征量被放大或缩小相同的倍数），PCA的输出特征向量都将不会发生变化。
　　
　　2）PCA不能阻止过拟合
　　表面上看PCA是降维了，因为在同样多的训练样本数据下，其特征数变少了，应该是更不容易产生过拟合现象。但是在实际操作过程中，这个方法阻止过拟合现象效果很小，主要还是通过规则项（正则化项）来进行阻止过拟合的。
　　
　　3）pca是一种无监督算法，没有类别信息
　　pca是选择投影后使得数据方差最大的方向来投影，假设就是方差越大，信息量越多。
　　

3.2 PCA的缺点

　　1）PCA 变换后会丧失数据的解释性
　　新的主成分并不是由实际系统产生的，因此在进行 PCA 变换后会丧失数据的解释性。如果说，数据的解释能力对你的分析来说很重要，那么 PCA 对可能就不适用了。
　　
　　2）信息少不意味着没用
　　当确定信息量少的那些维度对问题确实没帮助，降维肯定是好的，这使问题简化了。但是信息少往往不意味着没用，有时候信息少的那部分信息甚至是关键信息。比如组建篮球队考察身高这一项，天赋异禀的身高只有极少数，而这极少数恰好是最需要的。
　　
　　3）主成分变换对正交向量的尺度敏感
　　因此数据在变换前需要进行归一化处理。
　　
　　

四、PCA-Whitening　　

4.1 什么是Whitening

　　Whitening在一些文献中也叫sphering，目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：
　　(i) 特征之间相关性较低；
　　(ii) 所有特征具有相同的方差。
　　
　　
　　

4.2 PCA-Whitening的计算

　　通过前文可以知道，对原数据进行旋转（rotation ），或者说成映射（reflection），得到新坐标空间（基底）下的数据表示，就可以消除输入特征中各个特征项之间的相关性，同时保留了100%的方差。
　　回顾一下之前的例子：
　　

　　接下来只需要使每个特征项具有单位方差（unit variance）即可。我们可以直接使用
　　
　　作为缩放因子来缩放每个特征项。
　　具体计算公式如下：
　　
　　
　　绘制出 x _pcawhite 如下：
　　
　　总结来说，对一组数据进行Whitening操作，需要两个步骤：
　　第一步，通过PCA消除特征之间的相关性
　　
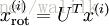
　　第二步，方差归一化
　　
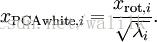
　　最后得到PCA-Whitening的数据，满足：PCA-Whitening后，不同的数据（特征向量）之间不相关并且具有单位方差。
　　
　　

五、ZCA-Whitening　　

5.1 ZCA-Whitening的计算

　　白化的目的是去相关和方差归一化，那么在上述PCA-Whtening中，只要达到这两个目的即可，计算方法并不唯一。换句话说，如果我们换一种方差归一化方法也是可以实现白化的，这就是下面要介绍的ZCA-Whitening。
　　
　　如果 R 是任意正交矩阵（any orthogonal matrix），即满足 RR^T = R^TR = I (说它正交不太严格， R 可以是旋转或反射矩阵)，那么 R 乘以 x_PCAwhite 仍然具有单位协方差。
　　在ZCA-Whitening中，令R=U（其中 U 是PCA白化中使用的特征向量矩阵） 。则我们定义ZCA白化的结果为：
　　

　　此时，数据的协方差矩阵依然是单位矩阵。
　　
　　

5.2 ZCA-Whitening与PCA-Whitening

　　ZCA 白化的全称是 Zero-phase Component Analysis Whitening。
　　从ZCA-Whitening的计算公式就可以看出：ZCA-Whitening相当于将经过PCA-Whitening后的数据重新变换回原来的空间。
　　
　　那么两者有什么联系和区别呢？
　　首先，PCA 白化将原数据变换（投影）到主成分轴上，这一步消除了特征之间的相关性；
　　其次，PCA 白化对每一个主成分轴上的数据进行缩放，使其方差为 1；
　　因为以上的线性变换是在主成分空间中完成的，为了使白化后的数据尽可能接近原数据，可以把处理过的数据再变换回原空间，也就是 ZCA 白化。
　　
　　

5.3 ZCA-Whitening的生物学基础

　　ZCA 白化是一种数据预处理方法，它将数据从 x 映射到 x_zcawhitening 。 事实证明这也是一种生物眼睛（视网膜）处理图像的粗糙模型。具体而言，当你的眼睛感知图像时，由于一幅图像中相邻的部分在亮度上十分相关，大多数临近的“像素”在眼中被感知为相近的值。因此，如果人眼需要分别传输每个像素值（通过视觉神经）到大脑中，会非常不划算。取而代之的是，视网膜进行一个与ZCA中相似的去相关操作（a decorrelation operation）（这是由视网膜上的ON-型和OFF-型光感受器细胞将光信号转变为神经信号完成的）。由此得到对输入图像的更低冗余的表示，并将它传输到大脑。
　　
　　

参考　

UFLDL-PCA

度量学习（Metric Learning）

PCA的数学原理（作者 张洋 | 发布于 2013-06-22）

数据分析过程中最有效的七种降维方法

PCA ，PCAWhitening ，ZCAWhitening

白化（Whitening）：PCA vs. ZCA