数学建模基于matlab模拟疫情SEIRS模型含Matlab源码 2214期

Posted 2022-12-06 海神之光

一、⛄SEIR模型简介

1 SEIR模型简介

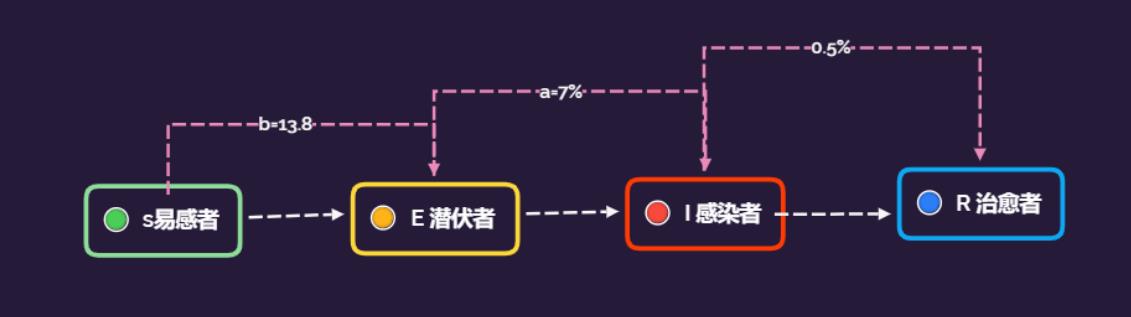
如果所研究的传染病有一定的潜伏期，与病人接触过的健康人并不马上患病，而是成为病原体的携带者，归入 E 类。此时有：

仍有守恒关系 S(t) + E(t) + I(t) + R(t) = 常数，病死者可归入 R 类。潜伏期康复率 γ1 和患者康复率 γ2 一般不同。潜伏期发展为患者的速率为 α。与 SIR 模型相比，SEIR 模型进一步考虑了与患者接触过的人中仅一部分具有传染性的因素，使疾病的传播周期更长。疾病最终的未影响人数 S∞ 和影响人数 R∞ 可通过数值模拟得到。

2 SEIR模型中的S\\E\\I\\R分别表示什么

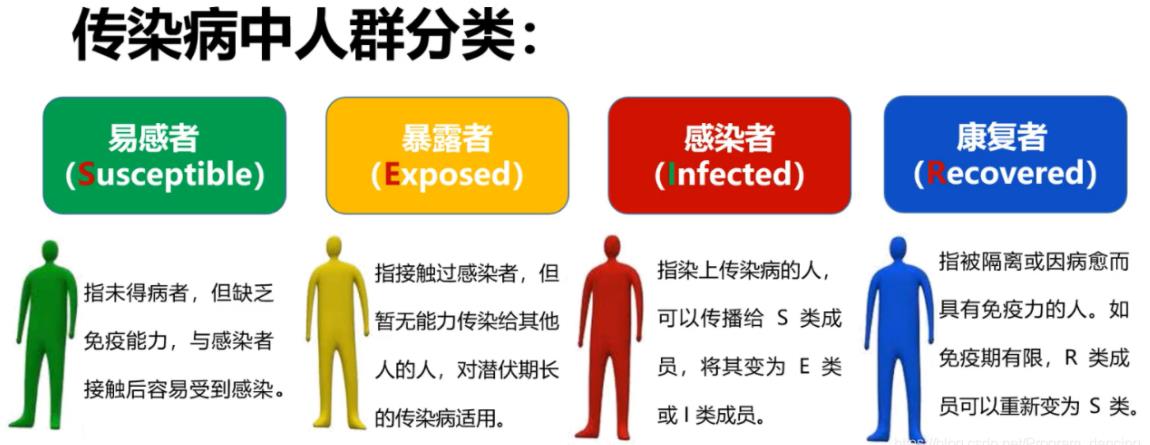
SEIR模型是传染病模型的一种，一般将传染病流行范围内的人群分为以下几类：
（1）S 类，易感者 (Susceptible)，指未得病者，但缺乏免疫能力，与感染者接触后容易受到感染；
（2）E 类，暴露者 (Exposed)，指接触过感染者，但暂无能力传染给其他人的人，对潜伏期长的传染病适用；
（3）I 类，感病者 (Infectious)，指染上传染病的人，可以传播给 S 类成员，将其变为 E 类或 I 类成员；
（4）R 类，康复者 (Recovered)，指被隔离或因病愈而具有免疫力的人。如免疫期有限，R 类成员可以重新变为 S 类。

3 为什么在“新冠”疫情模拟过程中选择SEIR模型作为基础模型
（1）原因一：SEIR模型相较于其他的几个传染病模型，多了几项内容。结合本次疫情分析，我们可以知道，“新冠”疫情是由为期14天的潜伏期的，而且当感染者经过治愈或是自身免疫成为治愈者后，体内产生抗体，不会再成为易感人群被感染者感染。所以在模型中E项是必须存在的。SEIR模型符合新冠疫情的传染特征。

（2）原因二：同时根现有的一些资料显示，可知，很多专业的研究团队都在使用该模型研究疫情的发展情况。例如：钟南山院士团队在Journal of Thoracic Disease《胸部疾病杂志》发表了题为“Modified SEIR and AI prediction of the epidemics trend ofCOVID-19 in China under public
health interventions”（基于SEIR优化模型和AI对在公共卫生干预下的中国COVID-19发展趋势预测）的文章。

4 使用该模型过程中的数据从何而来
通过上网搜索，我们小组找到了有关本次新冠疫情的数据（治愈率、死亡率）。以下内容引用自新京报网《关于新冠病毒的传播性，这五篇顶级论文都说了什么？》
（1）新冠病毒具有较低的致病性和中等传播性
此次的新冠病毒，是过去20年中新出现的第三种能够跨物种感染人的冠状病毒。此前两种分别是2003年的SARS冠状病毒和2014年的中东呼吸综合征冠状病毒（MERS)。
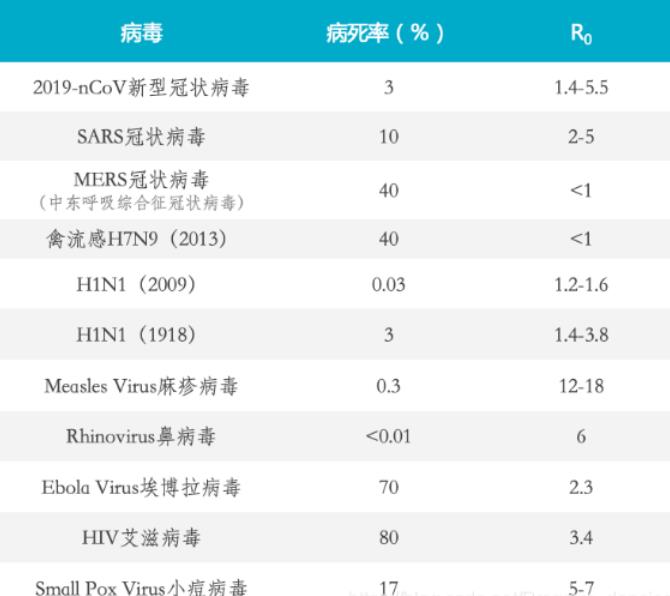
根据一篇发表在《Microbes and Infection》（《微生物与感染》）期刊上的论文《Pathogenicity and Transmissibility of 2019-nCoV—A Quick Overview and
Comparison with Other Emerging Viruses》（《2019-nCoV的致病性和传播性——快速概述和与其他新兴病毒的比较》）进行的分析对比，我们可以知道，新冠病毒无论是从病毒率或是R0均没有SARS病毒强。
但与2009年的甲型流感、2014年的中东呼吸综合症比，则有更强的感染性（即R0值更大）。这反映在感染的人数上，即是新冠肺炎的确诊病例更多。但整体来说，当前的新冠病毒似乎只是具有相对较低的致病性和中等传播性。

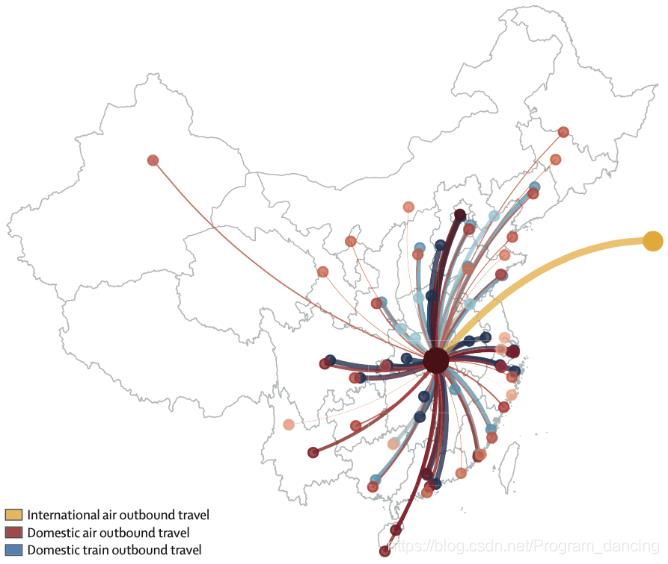
（2）其他城市疫情相对武汉具有1-2周的滞后性
根据另一篇于1月31日发表在《柳叶刀》上的论文《Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study》（《对源自中国武汉的2019-nCoV暴发的潜在国内和国际传播的预测和预测：一项模型研究》）认为，中国多个主要城市的疫情已经呈指数增长，但大概滞后于武汉暴发的大约1-2周。

5 该“新冠”疫情模拟小游戏中使用该SEIR模型的流程

⛄二、部分源代码

clear all; clc;
close all;
load(‘Infectious_data’, ‘T’, ‘X’); % load data generated by ODE45
load(‘prediction’); % Data from NN
X = X’;

% Generate training data
train_size = 20; % size of trainning data
x_idx = randperm(1000);
T_train = T(x_idx(1:train_size));
X_train = X(:,x_idx(1:train_size));
Y_train = X(:,x_idx(1:train_size)+1);

%% DMD Main
% Dynamic mode decomposition: Classic
Ad = Y_train * pinv(X_train);
[U,S,~] = svd(X_train,‘econ’);
eig_tru = sum(diag(S)>=0.01max(diag(S))); % Truncate eigenvalues to reduce noise
U = U(:,1:eig_tru);
Ad_til = U’AdU;
[W,D] = eig(Ad_til);
Omega = diag(log(diag(D)));
Phi = UW;
c = W \\ U’ * X(:,1);

X_DMD = zeros(size(X,1),length(T));
for t = 0:length(T)-1
X_DMD(:,t+1) = Phiexpm(Omegat)*c;
end

%% Koopman Main
% Define feature according to Brusselator
Psi = @(x) [x(1); x(2); x(3); x(4); x(5); x(6); x(7); x(1)*x(3); x(1)x(4); x(1)x(5)];
Psi_X = [];
Psi_Y = [];
for i = 1:train_size
Psi_X = [Psi_X,Psi(X_train(:,i))];
Psi_Y = [Psi_Y,Psi(Y_train(:,i))];
end
K = Psi_Y * pinv(Psi_X);
% Define observables g(x) = x
C = [eye(7), zeros(7,3)];
% Koopman decomposition
[W, Lambda] = eig(K);
V = CW;
Phi = @(x) pinv(W)Psi(x);
X_KOOP = zeros(size(X,1),length(T));
X_KOOP(:,1) = X(:,1);
% Prediction using Koopman
for i = 2:length(T)
X_KOOP(:,i) = VLambdaPhi(X_KOOP(:,i-1));
end

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社，2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社，2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社，2018.
[6]数学思想——1.SEIR模型

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除