数据结构--队列的实现（采用环形数组方式）

Posted 2022-12-05 大扑棱蛾子

在阅读本文之前请先阅读《数据结构–队列的实现（采用数组方式）》 ，本文是这篇文章的延续，如果您没有阅读前文，那么您在阅读本文时可能会一头雾水。

如果您已经打开了本文，也请耐心看完。本文将了两种实现环形数组的方法，也许您会觉得环形数组不就是一个环吗，很简单，不用看，想一想就明白了。但是我还是要建议您看一看，因为有很多细节需要注意。

原理概述

前文提到，使用数组实现队列的一个弊端。那么本文中将介绍如何去处理上文中提到的问题。在解决这个问题之前您需要先清楚模运算（$mod$），在Java中是%。如下：
$$\begin{gathered} 2\mathrm{m}\mathrm{o}\mathrm{d}3=2 \\ 4\mathrm{m}\mathrm{o}\mathrm{d}3=1 \end{gathered}$$

知道取模运算后我们就开始继续处理。

队头队尾的处理（方法一）

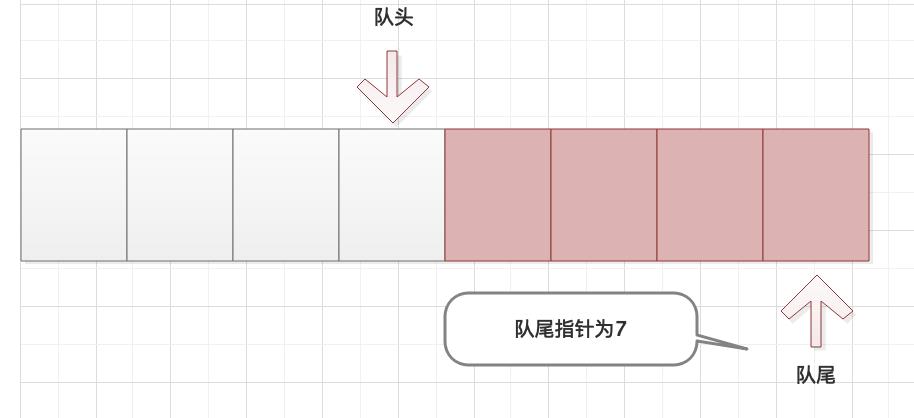
如上图，指针已达到队尾。如果还要继续添加元素，我们就需要判断数组中是否已满（后文中会讲如何来判断数组是否已满，或者说数组是否有空余位置）。发现数组未满，我们不是让队尾的指针重置为0，而是直接+1。

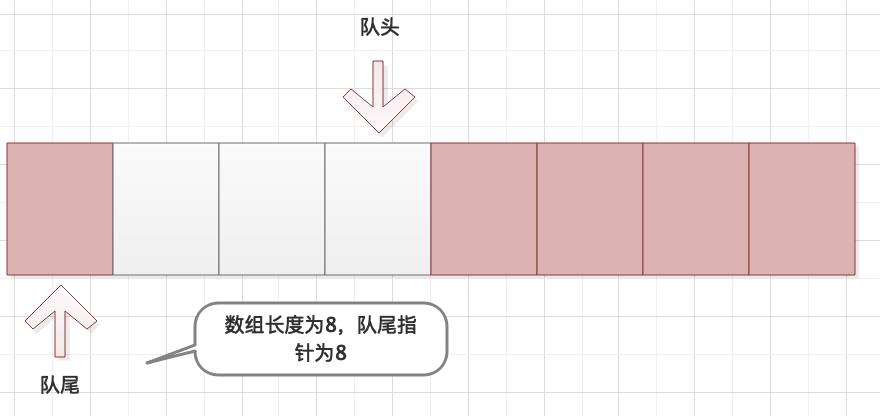
如图，队尾指针为8。我们通过模运算可以计算出指针在数组中的实际位置。8 % 8 = 0所以指针指向数组中的第一个元素。队头以此类推。这种方式就相当于将我们的数组无限延长了，队尾减去队头总是等于元素数量，如果队头等于队尾则元素数量为空。

队头数组索引位置 = 队头指针数 % 数组长度
队尾数组索引位置 = 队尾指针数 % 数组长度
0 <= 队尾指针数 - 队头指针数 <= 数组长度
队列为空判断：队尾指针数 = 队头指针数
队列满判断：队尾指针数 - 队头指针数 = 数组长度

但是这种方式也有个很明显的弊端，无论是int类型或者是long类型都有上限，一旦超出上限程序就会出现严重的BUG。

可以用下面的方法解决这个问题。
当队尾指针数大于 $n+1$ 倍的数组长度后，队尾指针和队头指针同时减去 $n$ 倍的数组长度。这样可以保证不会超限，同时还可以使用上面的算法来计算。

这里为什么是减去$n$倍，而不是$n+1$倍，请读者自己想一想。这个应该不难想到。

队头队尾的处理（方法二）

这里再介绍另外一种处理方式，这种方式才算是真正意义上的环形数组。如下图所示：

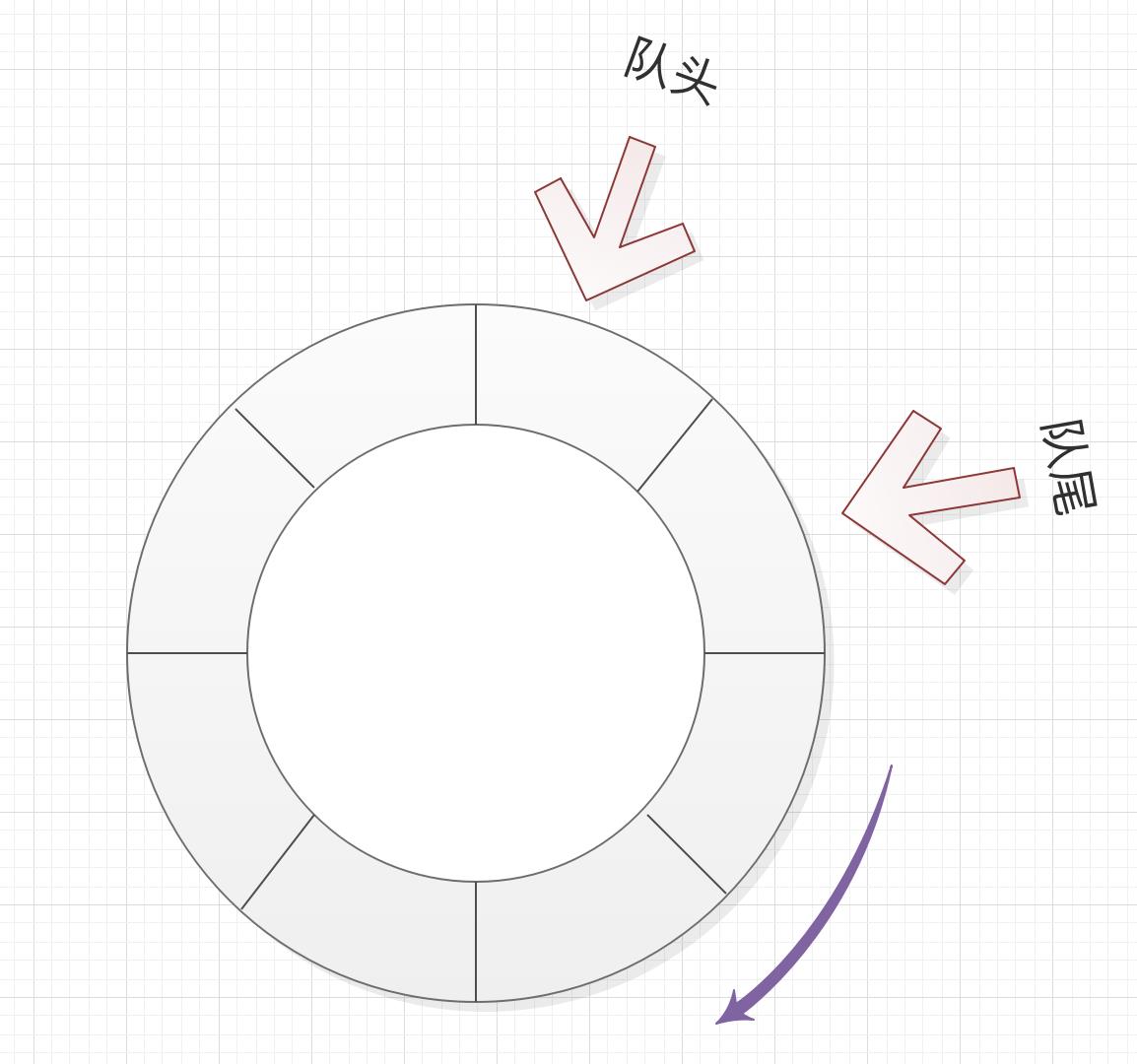
这种方法我们需要空出来一个位置，这个位置留个队头指针。

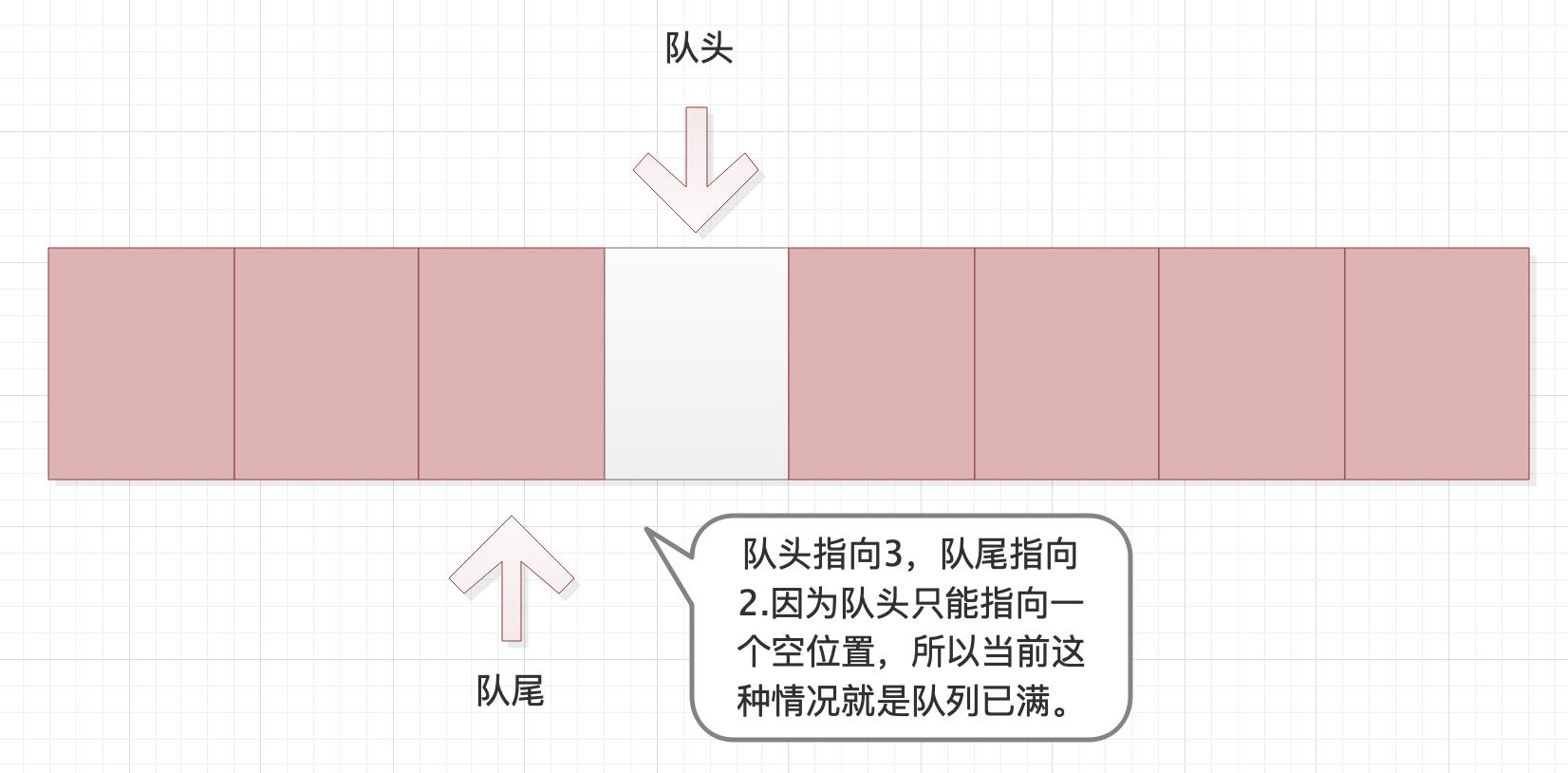
针对这种情况需要了解以下算法：

• 队列满：(队尾+1) % 数组长度 = 队头（其实是有一个空余位置，只是为了计算方便这个位置不使用）
• 队列空： 队头指针 = 队尾指针
• 队列中有效数据的个数：（队尾 + 数组长度 - 队头）% 数组长度（这个可能不太好理解）

关于队列中有效数据的个数的理解

如果您理解上面讲的东西，这部分可以不看

这里先不考虑队尾，试想一下队头后移一位则前面就空出来一个位置。当队头指向2的时候实际上是空出了3个位置。假如这时候的队尾指向了7（也就是数组尾部）那么就是$[7+1-(2+1)]=5$，也就是 队头指针-队尾指针。

如果队尾已经转了一圈了，那么这时候队尾的指针是小于队尾指针的，这就用到了上面的那种方法的一点思想。我们可以想象成在这个数组的后面又增加了一个数组，数组的索引要从0开始。如下图所示

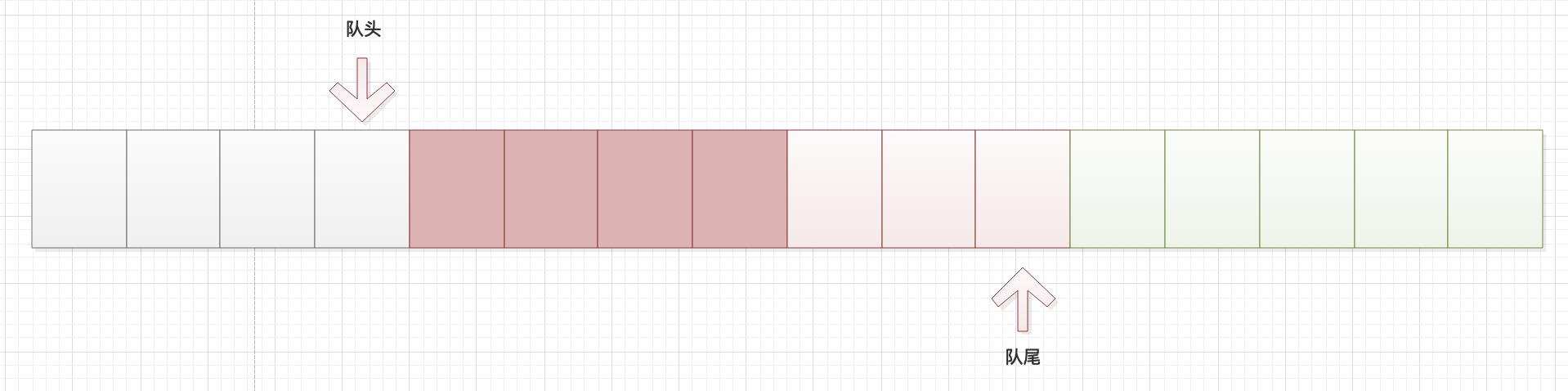
那么这个时候我们再计算有效数据个数的话就是：队尾指针+数组长度-队头。

综合以上两种情况，我们就可以得出（队尾 + 数组长度 - 队头）% 数组长度 就是有效数据的个数。

环形数组队列的实现

下面就上面讲的两种方式我们来逐一实现。

第一种

/**
 * 无限延长队头队尾的方式来实现数组队列
 *
 * @author jaune
 * @since 1.0.0
 */
public class InfinityArrayQueue<T> implements Queue<T> 

    final int maxSize;
    final T[] queueArray;
    private int front = -1;
    private int rear = -1;
    /**
     * 延长3倍后复位一次，最大长度不能超过@link Integer#MAX_VALUE / 2
     */
    private int baseN = 2;

    public InfinityArrayQueue(int maxSize) 
        this.maxSize = maxSize;
        this.queueArray = (T[]) new Object[maxSize];
    


    @Override
    public T peek() 
        if (this.isEmpty()) 
            throw new NoSuchElementException("队列为空");
        
        return this.queueArray[this.getRealFront() + 1];
    

    @Override
    public void push(T t) 
        if (this.isFull()) 
            throw new RuntimeException("队列已满，无法添加新的元素。");
        
        this.rear++;
        this.queueArray[this.getRealRear()] = t;
        // 每次push都需要检查指针
        if (this.rear > this.baseN * maxSize) 
            this.rear = this.rear - this.maxSize * (this.baseN - 1);
            this.front = this.front - this.maxSize * (this.baseN - 1);
        
    

    @Override
    public T pop() 
        if (this.isEmpty()) 
            throw new NoSuchElementException("队列为空");
        
        this.front++;
        T element = this.queueArray[this.getRealFront()];
        this.queueArray[this.getRealFront()] = null;
        return element;
    

    @Override
    public int size() 
        return this.rear - this.front;
    

    /**
     * 清空队列，并重置队头和队尾指针。
     */
    @Override
    public void clear() 
        for (int i = (this.front + 1); i <= this.rear; i++) 
            this.queueArray[i % this.maxSize] = null;
        
        this.front = -1;
        this.rear = -1;
    

    @Override
    public boolean isEmpty() 
        return this.rear == this.front;
    

    @Override
    public boolean isFull() 
        return this.size() == this.maxSize;
    

    /**
     * 获取真实的队头索引
     */
    private int getRealFront() 
        return this.front % this.maxSize;
    

    /**
     * 获取真实的队尾索引
     */
    private int getRealRear() 
        return this.rear % this.maxSize;
    

第二种

/**
 * 无限延长队头队尾的方式来实现数组队列
 *
 * @author jaune
 * @since 1.0.0
 */
public class CycleArrayQueue<T> implements Queue<T> 

    final int maxSize;
    final T[] queueArray;
    private int front = 0;
    private int rear = 0;
    /**
     * 延长3倍后复位一次，最大长度不能超过@link Integer#MAX_VALUE / 2
     */
    private int baseN = 2;

    public CycleArrayQueue(int maxSize) 
        // 为了保证队列中能放指定个数的元素，所以这里+1
        this.maxSize = maxSize + 1;
        this.queueArray = (T[]) new Object[this.maxSize];
    

    @Override
    public T peek() 
        if (this.isEmpty()) 
            throw new NoSuchElementException("队列为空");
        
        return this.queueArray[this.front + 1];
    

    @Override
    public void push(T t) 
        if (this.isFull()) 
            throw new RuntimeException("队列已满，无法添加新的元素。");
        
        this.rear = (this.rear + 1) % this.maxSize;
        this.queueArray[this.rear] = t;
    

    @Override
    public T pop() 
        if (this.isEmpty()) 
            throw new NoSuchElementException("队列为空");
        
        this.front = (this.front + 1) % this.maxSize;
        T element = this.queueArray[this.front];
        this.queueArray[this.front] = null;
        return element;
    

    @Override
    public int size() 
        return (this.rear + this.maxSize - this.front) % this.maxSize;
    

    /**
     * 清空队列，并重置队头和队尾指针。
     */
    @Override
    public void clear() 
        for (int i = 0; i < this.maxSize; i++) 
            this.queueArray[i] = null;
        
        this.front = -1;
        this.rear = -1;
    

    @Override
    public boolean isEmpty() 
        return this.rear == this.front;
    

    @Override
    public boolean isFull() 
        return (this.rear + 1) % this.maxSize == this.front;
    

这两种方式的测试代码就不在这里赘述了，跟前文中的差不多。主要是掌握环形数组的核心思想。