AtCoder Regular Contest 084

Posted 2022-12-05 佐鼬Jun

Snuke Festiv

题意：

给定长度为$N$的三个数组 A,B,C，现在让你分别从A,B,C中各选一个数，要保证A中选的数严格小于从B中选的数，从B中选的数要严格小于从C中选的数，即$A_i<B_j<C_k$，问有多少种选法？

思路：

先枚举每个$B_j$，算出每个$B_j$能搭配多少个$C_k$,这个用二分找即可,然后把这些数记录下来，求一边后缀和$su{m}_j$,然后再枚举每个$A_i$算出有多少个$B_j$符合要求，然后算出$B_j+B_{j+1}+....B_N$的和，这个和就是前面提前预处理出来的后缀和，然后累加即可

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
#define ll long long
int a[N], b[N], c[N];
int n;
ll res;
ll sum[N];
int main() 
    cin >> n;
    for (int i = 1; i <= n; i++) 
        cin >> a[i];
    
    for (int i = 1; i <= n; i++) 
        cin >> b[i];
    
    for (int i = 1; i <= n; i++) 
        cin >> c[i];
    
    sort(a + 1, a + 1 + n);
    sort(b + 1, b + 1 + n);
    sort(c + 1, c + n + 1);
    for (int i = 1; i <= n; i++) 
        int now = b[i];
        int t = upper_bound(c + 1, c + n + 1, now) - c;
        sum[i] = n - t + 1ll;
    
    for (int i = n; i >= 1; i--) 
        sum[i] += sum[i + 1];
    
    for (int i = 1; i <= n; i++) 
        int now = a[i];
        int t = upper_bound(b + 1, b + n + 1, now) - b;
        res += sum[t];
    
    cout << res << endl;

Small Multiple

题意:

给定一个函数$f(n)$为$n$的各位数字之和，现在给定一个$n$，让你算出$n$的所有倍数中，所有$kn$，$f(kn)$的最小值

思路：

单纯的枚举所有的$n$的倍数，在把各位数求和，最后取最小值，一定会超时，数量范围太大。换个思路，去看一个数的各个位数之和是如何算出来的。
先仅看个位的话，$1$的位数和位$1$，$2$就是$1+1$，…$9$就是$1+8$，
再看十位的话，要想快速形成$10$,一定是$10\times 1$而不是$1+9$…
…

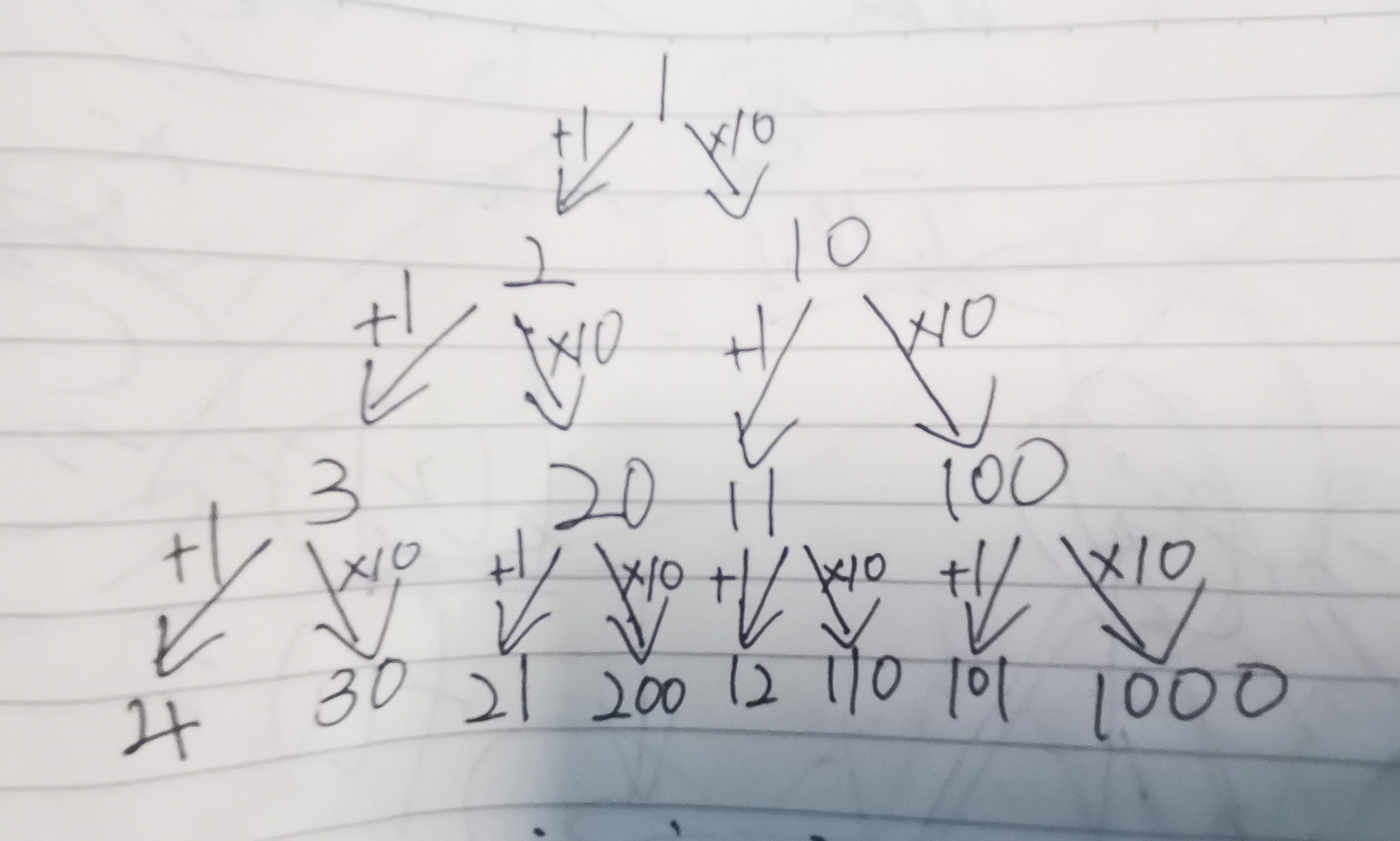
会发现在这个二叉树结构中，$+1$代表着各位数和$+1$(在不进位的情况下)，$\times 10$代表着各位数和不变，所以在这个树形结构中，我们只要找到各位数最小的且这个数是$n$的倍数的数，就是答案。在这个树形结构中，重复出现的数的就拿最小的各位数和处理即可。此时只要构造出这个树形结构即可，$+1$代表边权为$1$，$\times 10$代表边权为$0$，只要在搜索过程中第一次出现$n$的倍数，那么这个数就是答案，对于这个搜索结构，边权只有$0和1$,所以就可以用双端队列广搜即可，也可以建边最短路，是一样的效果。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
#define int long long
typedef pair<int,int> PII;
bool vis[N];
int k;
int BFS() 
    deque<PII> q;
    q.push_back(1ll,1ll);
    
    while(q.size()) 
        auto t=q.front();
        q.pop_front();
        int now=t.first;
        int step=t.second;
        if(vis[now]) continue;
        vis[now]=1;
        if(now==0) 
            return step;
        
        if(!vis[(now+1)]) 
            q.push_back((now+1),step+1);
            //vis[(now+1)]=1;
         
        if(!vis[(10*now)%k]) 
            q.push_front((10*now)%k,step);
            //vis[(10*now)%k]=1;
        
    
    return 0;

signed main() 
    cin>>k;
    int res=BFS();
    cout<<res<<endl;

Finite Encyclopedia of Integer Sequences.

题意：

现在会有很多个序列长度在$1到N$之间，且序列内的数字大小在$1到K$之间的数，总共会出现$X$个序列(未知的),现在在按照字典序排完序后，让你输出位于$\lceil X/2\rceil$的序列

思路：

对于$K$为偶数的情况，可以发现以每个数字为开头的序列的总数都是一样的，所以以取就是相当于$K$个数中取第$\lceil K/2\rceil$号数一样，因为是整个序列的中间，所以一定是以$K/2$为开头的序列当中，后面的$N-1$个数都是$K$的情况。
对于$K$为奇数的情况，因为以每个数字为开头的序列的总数都是一样的，所以答案序列的开头一定是$\lceil K/2\rceil$，由于有长度小于$N$的序列在前面干扰，所以不好做判断，先假设当前这个数引导的只有以长度为$N$的序列，那么此时，其中间序列一定是$\frac{K+1}{2}\frac{K+1}{2}\frac{K+1}{2}.......$共$N$个。由于大于$\frac{K+1}{2}$的数和小于$\frac{K+1}{2}$的数的数量是一样的，所以就代表着这些数都有对标的比它大的数或者比它小的数，例如，
$2$
$21$ $211$ $212$ $213$
$22$ $221$ $222$ $223$
$23$ $231$ $232$ $233$
$21$ 对标 $23$ $211$ 对标以上是关于AtCoder Regular Contest 084的主要内容，如果未能解决你的问题，请参考以下文章

AtCoder Regular Contest 101

[Atcoder Regular Contest 060] Tutorial

AtCoder Regular Contest 101

AtCoder Regular Contest E - Or Plus Max

AtCoder Regular Contest 146 C Even XOR题解

AtCoder Regular Contest 146 C Even XOR题解