海量数据处理-重新思考排序

Posted 2022-12-04 xiaoranone

海量数据处理－－重新思考排序（1）

海量数据处理常用技术概述

如今互联网产生的数据量已经达到PB级别，如何在数据量不断增大的情况下，依然保证快速的检索或者更新数据，是我们面临的问题。
所谓海量数据处理，是指基于海量数据的存储、处理和操作等。因为数据量太大无法在短时间迅速解决，或者不能一次性读入内存中。

在解决海量数据的问题的时候，我们需要什么样的策略和技术，是每一个人都会关心的问题。今天我们就梳理一下在解决大数据问题
的时候需要使用的技术，但是注意这里只是从技术角度进行分析，只是一种思想并不代表业界的技术策略。
常用到的算法策略

1. 分治：多层划分、MapReduce
2. 排序：快速排序、桶排序、堆排序
3. 数据结构：堆、位图、布隆过滤器、倒排索引、二叉树、Trie树、B树，红黑树
4. Hash映射：hashMap、simhash、局部敏感哈希

海量数据处理–重新思考排序(1)

定义排序

排序:
　　将一组无序的集合，根据某个给定的条件，将其变成有序的方法就是排序。从这个我给出的不严谨的定义中排序是方法，目的是让原来无序的集合满足条件有序。
　　这里我们基于海量数据的考虑重新思考排序，不会详述每一种排序方法的原理，主要面向的是如何在海量数据情况下使用排序方法。

常用的排序方法:
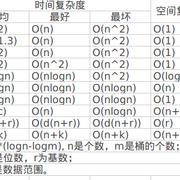
　　插入排序，选择排序，冒泡排序，希尔排序，快速排序，归并排序，堆排序，桶排序，计数排序，基数排序。
下面给出几种排序算法的简单介绍图。
　　　　　

既然有这么多的排序方法，我们可以直接读取数据到内存中直接调用语言中封装好的排序方法即可。但是数据量很大，不能将数据同时读入内存。
这就出现了所有的外排序，我们可以用归并排序的思想来解决这个问题，也可以基于数据范围用"计数排序"的思想来解决。
排序真的很重要吗？我一直相信一句话:没有排序解决不了的问题。这里给出几个需求，例如:

• 取最大的ｋ个数，直接降序排序取前ｋ个即可；
• 推荐、搜索业务，我们也可以直接排序(精度不高)
• 二分查找之前也要求数据有序

但是在这里我们不讲排序，只说排序中用到的思想，以及在海量数据处理的过程中，如何用到的排序。依然接着
上次的文章，我们求top k的时候，最后用到了一个数据结构，叫做堆，堆可以找个top k，就能找到n个数中的
top n，这样就是有序，叫做堆排序。

堆排序

在top k中我们用到了一个数据结构堆(有最大堆和最小堆)，这里就先介绍一下这个数据结构的性质，基于最大
堆进行介绍。堆是一个完全二叉树，对于任意的节点，我们可以使用数据来表示最大堆，设置下标从0开始, 满足以下性质:

• root > left && root > right. (左右节点存在)
• 根节点:root_index; 左孩子节点:left_index; 右孩子节点:right_index
• left_index = root_index * 2 + 1
• right_index = root_index * 2 + 2
• root_index = (*_index - 1) / 2

在堆的数据结构进行增删改查的过程中，我们始终维护堆的数据结构，定义MaxheapFy(int *A, int i)表示维护第i个
节点满足最大堆的性质，注意这里没有考虑到泛型编程，正常应该提供一个比较方法的函数，让使用者自己设置比较方式。
从下面的伪代码中，我们可以知道对于一个大小为n的堆，维护一次堆的性质，最坏时间为O(logn)，但是必须保证
在改变之前，他是满足堆的性质的。

void MaxheapFy(int *A,int i) 
    // i 要在A的范围之内，
    assert(i >= 0);
    assert(i < n) // 堆的大小
    l = LEFT(i), r = RIGHT(i); // 得到左右子节点，如果存在
    now = i;

    // 找到左右孩子的最大值
    if(l<=heapsize&&A[l]>A[now])
        now=l;//交换A[l]和A[i]，并递归维护下一个当前结点now
    
    if(r<=heapsize&&A[r]>A[now])
        now=r;//交换A[l]和A[i]，并递归维护下一个当前结点now
    

    if(now != i)  // 交换，递归维护
        swap(A[i], A[now]);
        MaxheapFy(A, now);
    

基于上面的这个维护的性质，我们可以直接对于长度为n的数组建立最大堆，我们知道当只有一个元素的时候，一定满足最大堆的性质，
基于这个性质，我们对于长度为n的数组A，从 n / 2向前维护每一个节点的性质，就可以得到最大堆.从下面给出的最大堆
的构建代码，我们可以分析建堆的时间复杂度是O(nlogn).因为每次维护是O(logn),维护n次，(这里计算时间复杂度的时候，忽略常数系数)。

void BuildMaxHeap(int *A,int n)//A[1..n]
    heapsize=n;//全局变量，表示最大堆的大小
    for(int i=n/2;i>=1;i--)//从n/2..1维护堆中每个节点的最大堆性质：结点的值大于起孩子的值
        MaxheapFY(A,i);
    

建成最大堆之后，从最大堆的性质我们知道，A[0]一定是最大值，如果要堆A升序排序，就可以swap(A[0], A[n-1]);
继续维护A[0],直到堆中只是一个元素，这就完成了堆排序。从这个思路出发，对于top k问题，我们为什么要维护一个
最小堆呢，因为我们要过滤所有的数据，保证每次弹出一个最小值，之后剩下的k个一定是top k的最大值，但是这k个不一定
有序，如果需要我们可以堆这k进行任何排序，因为我们通过过滤，数据已经很少了，时间复杂度就是从n个中过滤出来k个。
首先任选k个构建最小堆, 时间复杂度O(klogk), 用最小堆过滤n-k个数字，每次维护堆的性质，时间O((n-k)logk).
总的时间复杂度O(klogk + (n-k)logk)。(注意当k多大时，我们不在使用堆的数据结构，这里留给读者计算)。

void HeapSort(int *A,int n)
    BuildMaxHeap(A,n);//建立最大堆
    for(int i=n;i>=2;i--)
        //cout<<A[1]<<" ";
        swap(A[1],A[i]);//交互A[1]和A[i],使得A[i]中为当前最大的元素
        heapsize--;//堆大小减去1，便于下次操作去掉已经排好序的元素
        MaxheapFY(A,1);//此时A[1]不一定满足最大堆的性质，重新维护下标1的最大堆的性质
    

我们可以知道堆的使用可以很好的找到top k，堆使用场景都有什么呢？这里我们给出工业界常用到的使用场景。
推荐系统大家都很了解，例如手机百度、今日头条等会推荐用户喜欢的新闻，在推荐系统中就有用到堆。为了很好的了解到堆的
应用，我简单介绍一个简化推荐系统，至少有recall和rank两个部分，在recall(召回的阶段))，对于使用手机百度的用户，
当你进行一次刷新的时候，后天会根据的你各种profile等静态和动态的特征，请求后端，后端会从多个方面召回一可能感兴趣
的文章，例如基于地域，性别，当天热门，学历，浏览记录等，这样就会返回多个带有权重的队列，下一步会从这多个队列中，选择
100个得分最高的传到下一层，这个过程中就要用到堆。这里用到的是大根堆。

问题抽象
例如我们有100个有序(降序)的数组，现在从这个100个数组中找到最大的k个元素。这就是上述问题的抽象。使用100路归并(后面的归并排序)。
用一个大小为k的最大堆，每次弹出一个最大值，记录是那个队列中的值，直到出现k个数，就结束。这里里面的两个思想，

• 归并，不能处理的大问题，分成多个小问题并行处理，之后归并结果，比如外排序
• 堆，帮助我们找到top k，k要相对n较小。

参考:
数据结构: 构建和使用堆
《算法导论》第六章：堆排序
《编程之美：面试与算法心得》