多核支持向量机原理及实现

Posted 2022-12-03 SSyangguang

了解非线性支持向量机模型后，应该对支持向量机的原理与核技巧都有掌握，本文在传统非线性支持向量机基础上向大家介绍多核支持向量机，这里就不对支持向量机原理与核函数花费太多笔墨了，主要介绍将单核支持向量机转换为多核支持向量机的思想。原理介绍完之后会提供Python实现的思路。

1. 核函数

对于非线性问题，使用直线无法将正负实例分开，但是可以使用非线性模型将其分离。如果使用超曲面可以将正负实例则称这个问题是非线性问题，往往需要一个非线性变换将非线性问题转换为线性问题。可以通过映射函数，将原空间上的点映射到新空间上的点，然后在新空间中使用线性学习方法得到分类模型。通常情况下通过映射函数计算一个核函数不容易，而直接计算核函数是较为容易的方法，《统计学习方法》第一版中例7.3就可以帮助我们理解核函数与映射函数的关系。

核函数为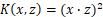，两个样本点分别为，

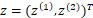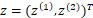
那么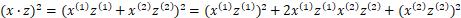

取映射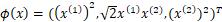

容易验证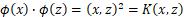

上式中，原来的每个样本点二维表示，包含两个特征，而经过映射函数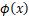的变换后，由原来的两个特征变为三个特征，样本从二维升为三维。对偶函数的目标函数中内积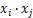可以用核函数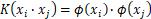。这个就是核函数的基本作用。可以得到支持向量展开式（support vector expansion），如下式所示。

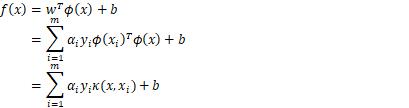
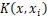指核函数，上式显示模型的最优解可以通过训练样本的核函数展开，这里也是多核支持向量机程序实现的基础。

2. 多核支持向量机

多核支持向量机在传统支持向量机的基础上，将多个核函数使用线性组合方式进行融合，然后基于该核函数训练一个支持向量机分类器，解决了如下的凸二次优化问题。

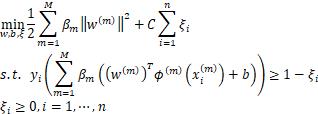
其中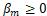, , 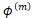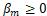分别为第m个模态超平面方程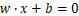中的法向量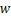、映射方程和改模态下的核函数融合系数，它的对偶形式如下。

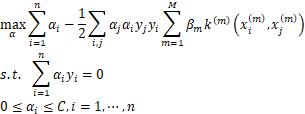
其中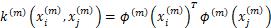是第m个模态中两个训练样本之间的核函数形式。而在训练集中核函数的形式可以写为如下形式。

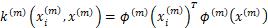
其中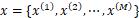表示测试集的样本，上式表示测试集中新样本和训练集中每一个样本的核函数计算形式。这样就可以得到决策方程为

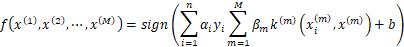
实际使用中，先计算各个模态的训练集核矩阵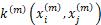，通过线性组合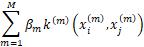将不同模态的核函数进行融合。再计算各个模态的测试集核矩阵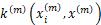，使用和训练集相同的核矩阵融合系数对核矩阵进行融合，同时要满足融合系数的和为1，即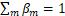。支持向量展开式的结论中，分类器的最优解可以通过核函数展开，因此直接使用训练集得到的核矩阵作为支持向量机输入，即可学习一个多核支持向量机分类模型，对测试集样本进行分类时，直接将测试集核矩阵作为输入，就可以得到它们的分类结果了。关于核函数融合的过程见下图。

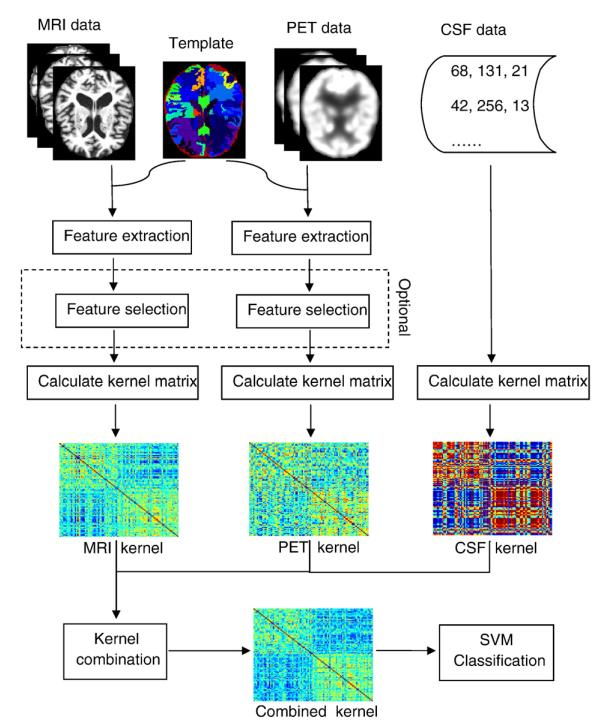
上图是论文Multimodal classification of Alzheimer's disease and mild cognitive impairment中的多模态核函数融合过程，由MRI、PET和CSF三种模态得到了三个核函数，然后使用线性组合方式将这三个核函数进行融合就得到了融合核矩阵，使用这个矩阵作为输入特征进行训练就可以得到一个多核支持向量机分类模型。

3. 多核支持向量机的Python实现过程

3.1 使用scikit-learn库实现多核支持向量机

对于多核支持向量机当然起码得有两种核函数吧。这里列举较为常用的linear、poly和rbf核函数。这里假定已经得到由各个核函数计算得到的核矩阵kernel_mat，那么进行多核支持持向量机的过程如下。

for i in range(grid_num):

weight1 = i * 0.1

weight2 = 1 - weight1


acc_fold = []

for fold in range(kfold):

# 计算第一种模态的训练集核矩阵与测试集核矩阵

fmri_train = calckernel(kernel_type='rbf', kernel_para=1, X_train=mat1)

fmri_test = calckernel(kernel_type='rbf', kernel_para=1, X_train=mat1, X_test=mat2)


# 计算第二种模态的训练集核矩阵与测试集核矩阵

dti_train = calckernel(kernel_type='poly', kernel_para=3, X_train=mat1)

dti_test = calckernel(kernel_type='poly', kernel_para=3, X_train=mat1, X_test=mat2)


# 进行双模态核矩阵融合

train_kernel = weight1 * fmri_train + weight2 * dti_train

test_kernel = weight1 * fmri_test + weight2 * dti_test


# svm训练

from sklearn.svm import SVC

svm = SVC(kernel='precomputed', C=C, probability=True)

svm.fit(train_kernel, y_train)

pred = svm.predict(test_kernel)

3.2 程序解释

上面的程序使用网格搜索法，对每一种融合系数组合都进行svm的训练与分类，最后得到每种组合下的分类结果，进而可以使用skleaen.metrics中的函数计算各种分类指标。

因为融合系数相加为1，所以每种融合系数的范围是0到1的，这里设定搜索参数的个数grid_num，然后使用循环对每种融合系数组合都进行多核SVM训练。

mat1和mat2可以分别表示训练集和测试集的特征矩阵，维度分别为n×d和m×d。有了特征矩阵后就可以计算核矩阵了，我这里是自己写了calckernel函数直接就可以得到核矩阵，各位可以通过调库或者直接自己写来实现核函数的部分。对于训练集核矩阵，只需要传入训练集特征矩阵即可，测试集核矩阵的计算则同时需要训练集和测试集的特征矩阵。计算完每种模态的核矩阵后通过weight1和weight2对两种模态的核矩阵进行线性融合，得到的训练集核矩阵维度为n×n，测试集核矩阵为m×n。

使用scikit-learn库训练时，参数设置这里除了SVM一般的超参数外还需要设置核函数的类型，参考https://scikit-learn.org/stable/modules/svm.html#kernel-functions。自定义kernel时有两种方式，一种是自定义核函数方程，单独写一个核函数后，同样使用fit()就能对数据进行学习了。另一种方式是定义Gram矩阵，也就是我们所使用的方法，需要将kernel设置为’precomputed’，然后SVM训练过程在fit()中将参数设置为上述的训练集核矩阵train_kernel和类别标签y_train，分类过程同样是用predict()函数，将参数设置为上述的测试集核矩阵test_kernel和类别标签y_test。Sklearn的官方文档的示例如下：

>>> import numpy as np

>>> from sklearn.datasets import make_classification

>>> from sklearn.model_selection import train_test_split

>>> from sklearn import svm

>>> X, y = make_classification(n_samples=10, random_state=0)

>>> X_train , X_test , y_train, y_test = train_test_split(X, y, random_state=0)

>>> clf = svm.SVC(kernel='precomputed')

>>> # linear kernel computation

>>> gram_train = np.dot(X_train, X_train.T)

>>> clf.fit(gram_train, y_train)

SVC(kernel='precomputed')

>>> # predict on training examples

>>> gram_test = np.dot(X_test, X_train.T)

>>> clf.predict(gram_test)

array([0, 1, 0])

参考

[1] https://stats.stackexchange.com/questions/239008/rbf-kernel-algorithm-python

[2] https://intellipaat.com/community/22796/how-to-use-a-custom-svm-kernel

[3] https://stackoverflow.com/questions/2474460/precomputed-kernels-with-libsvm-in-python

[4] https://scikit-learn.org/stable/modules/svm.html#kernel-functions

[5] Zhang, Daoqiang, et al. "Multimodal classification of Alzheimer's disease and mild cognitive impairment." Neuroimage 55.3 (2011): 856-867.

[6] 李航. 统计学习方法[M]. 清华大学出版社, 2012.

[7] 周志华. 机器学习[M]. 清华大学出版社, 2016.