推荐系统PNN模型（Product-based Neural Networks）

Posted 2022-12-03 天泽28

推荐系统（九）PNN模型（Product-based Neural Networks）

推荐系统系列博客：

1. 推荐系统（一）推荐系统整体概览
2. 推荐系统（二）GBDT+LR模型
3. 推荐系统（三）Factorization Machines（FM）
4. 推荐系统（四）Field-aware Factorization Machines（FFM）
5. 推荐系统（五）wide&deep
6. 推荐系统（六）Deep & Cross Network（DCN）
7. 推荐系统（七）xDeepFM模型
8. 推荐系统（八）FNN模型（FM+MLP=FNN）

PNN模型（Product-based Neural Networks）和上一篇博客介绍的FNN模型一样，都是出自交大张伟楠老师及其合作者，这篇paper发表在ICDM’2016上，是个CCF-B类会议，这个模型我个人基本上没听到过工业界哪个公司在自己的场景下实践过，但我们依然可以看看这篇paper的成果，也许能为自己的业务模型提供一些参考借鉴意义。通过这个模型的名字Product-based Neural Networks，我们也基本可以略知PNN是通过引入product（可以是内积也可以是外积）来达到特征交叉的目的。

这篇博客将从动机和模型细节两方面进行介绍。

一、动机

这篇paper主要改进的是上一篇博客介绍的FNN，FNN主要存在两个缺点：

1. DNN的embedding层质量受限于FM的训练质量。
2. 在FM中进行特征交叉时使用的是隐向量点积，把FM预训练得到的embedding向量送入到MLP中的全链接层，MLP的全链接层本质上做的是特征间的线性加权求和，即做的是『add』的操作，这与FM有点不太统一。另外，MLP中忽略了不同的field之间的区别，全部采用线性加权求和。

论文原文为：

1. the quality of embedding initialization is largely limited by the factorization machine.、
2. More importantly, the “add” operations of the perceptron layer might not be useful to explore the interactions of categorical data in multiple fields. Previous work [1], [6] has shown that local dependencies between features from different fields can be effectively explored by feature vector “product” operations instead of “add” operations.

其实个人认为FNN还有个很大的局限性：FNN是个两阶段训练的模型，并不是个data-driven的end-to-end模型，FNN身上还是有浓厚的传统机器学习的影子。

二、PNN模型细节

2.1 PNN模型整体结构

PNN的网络结构如下图所示（图片摘自原论文）

PNN模型的核心在于product layer，也就是上图中的product layer pair-wisely connected这一层。但不幸的是，原论文中给出的这张图隐藏了其中最重要的信息，看完上图的第一印象是product layer由$z$和$p$组成，然后直接送到上层的$L1$层。但实际上不是这样的，论文中所描述的是：$z$和$p$在product layer分别又进行了全连接层的转换，分别将$z$和$p$映射成了$D_1$维度输入向量 $l_z$和 $l_p$（$D_1$为隐藏层的神经元个数），然后再将 $l_z$和 $l_p$ 叠加，然后再送入到$L_1$层。
所以，我自己把product layer重新画一下，看起来更详细的PNN模型结构，如下图所示：

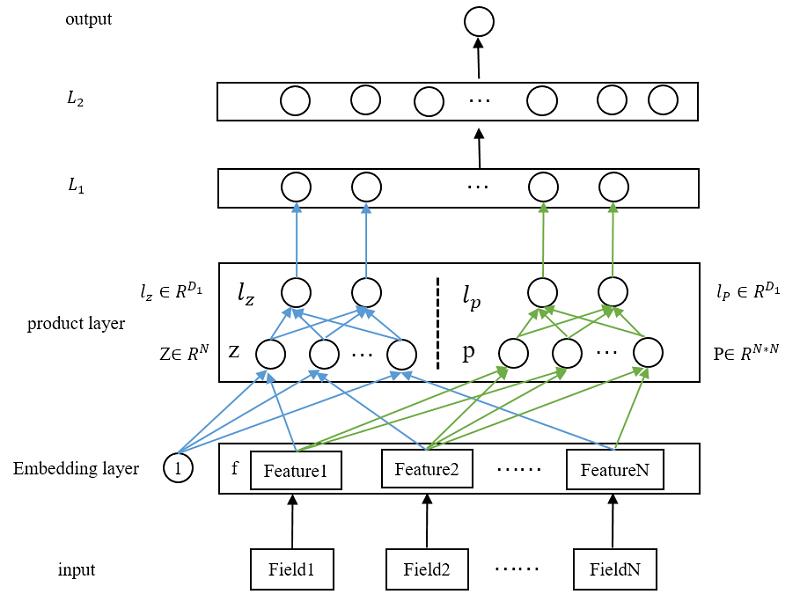
上面这个图基本上很清晰的把PNN的整体结构及核心细节都展示出来了。我们自底向上的看一看每一层

• 输入层
  原始特征，没什么好说的。论文里为$N$个特征。
• embedding层
  也没什么好说的，就一普通的embedding层，维度为$D_1$。
• product 层
  整篇论文的核心，这里分为两部分：$z$和$p$，这两个都是从embedding层得到的。
  【1. 关于$z$】
  其中$z$是线性信号向量，其实就是直接把$N$个特征的embedding向量直接copy过来，论文里用了个常量1，做相乘。论文中给出了形式化的定义：
  $$z=(z_1,z_2,z_3,...,z_N)\triangleq (f_1,f_2,f_3,...,f_N)\text{\hspace{1em}(1)}$$
  其中$\triangleq$为恒等，所以$z$的维度为$N\ast M$。
  【2. 关于$p$】
  $p$这里是真正的交叉操作，关于如何生成$p$，论文里给出了形式化的定义：$p_{i,j}=g(f_i,f_j)$，这里的$g$理论上可以是任何映射函数，论文给出了两种映射：内积和外积，分别对应着IPNN和OPNN。因此：
  $$p=p_{i,j},i=1,2,...,N;j=1,2,...,N\text{\hspace{1em}(2)}$$
  所以，$p$的维度为$N^2\ast M$。
  【3. 关于$l_z$】
  有了$z$之后，通过一个全连接网络，如上图中product layer中蓝色线部分，最终被映射成$D_1$维（隐藏层单元的个数）的向量，形式化的表示为：
  $$l_z=(l_z^1,l_z^2,...,l_z^k,...,l_z^{D_1})l_z^k=W_z^k\odot z\text{\hspace{1em}(3)}$$
  其中，$\odot$为内积符号，定义为：$A\odot B\triangleq {\sum }_{i,j}{A}_{ij}{A}_{ij}$，因为$z$的维度为$N\ast M$，所以$W_z^k$的维度也为$N\ast M$。
  【4. 关于$l_p$】
  和$l_z$一样，通过一个全连接网络，如上图中product layer中绿色线部分，最终被映射成 D 1 D_1 PNN网络（Product-based Neural Network）

  PNN网络（Product-based Neural Network）

  19推荐系统8PNN模型——加强特征交叉能力

  值得借鉴：360推荐系统架构演进

  （读论文）推荐系统之ctr预估-Wide＆Deep模型解析

  推荐系统系列：Deep Crossing理论与实践