OFDM基本原理

Posted 2022-12-03 bobuddy

目录
1.OFDM的产生和发展
2.串并转换
3.子载波调制
4.DFT的实现
5.保护间隔、循环前缀和子载波数的选择
6.加窗技术
7.RF调制
8.OFDM基本参数的选择
OFDM是一种特殊的多载波传输方案，它可以被看做是一种调制技术，也可以被当作一种复用技术。多载波传输把数据流分解成若干子比特流，这样每个字数据流将具有低比特率，从而降低速率符号并行发送的传输系统。它也是对多载波调制（MCM）的一种改进。它的特点是各个子载波相互正交，所以扩频后的频谱可以相互叠加，从而减小了子载波间的相互干扰，还大大的提高了频谱利用率。并且OFDM系统能够很好地对抗频率选择性衰落和窄带干扰。

正交频分复用(OFDM)技术与已经普遍应用的频分复用(FDM，Frequency Division Multiplexing)技术十分柑似。与FDM基本原理相同，OFDM把高速的数据流通过串并变换，分配到速率相对较低的若T干个频率子信道中进行传输，不同的是，OFDM技术史好地利用了控制方法，使频谱利用率有所提高。OFDM与FDM的主要差别有以下几方面:

(1) 在常规的广播系统中，每一个无线基站在不同的频率上发送信号，有效地运用FDM来保证每个站点的分隔，广播系统中的每一个站点没有任何的同位或同步。但使用OFDM传播技术，譬如DAB，从多个无线基站来的信息信号被组合成个单独的复用数据流，这些数据是由多个子载波密集打包组成的，然后将在OFDM体系中传输，在OFDM信号内的所有子载波都在时间和频率上同步，使子载波之间的干扰被严格控制。这些复用的子载波在频域中交锆重叠，但因为调制的正交性采用循环前缀作为保护间隔，所以不会发生载波间干扰(ICI，Inter-Carrier lnterference)。

(2) 对传统的FDM系统而旨，传输的信号需要在两个信道之间存在较大的频率问隔即保护带宽来防止干扰，这降低了全部的频谱利用率。然而应用OFDM的子载波正交复用技术大大减少了保护带宽，提高了频谱利用率，如图1所示，在早期的OFDM系统中，斧子载波采用正交滤波器将信道分成多个子信道，但要用很多的滤波器,尤其是当路数增多的时候。1971年，Weinstein及Ebert等将DFT应用在多载波传输系统中，从而很方便地实现了多路信号的复合和分解。OFDM系统的一个重要优点就是可以利用快速傅里叶变换实现调制和解调，从而大大简化系统实现读的复杂度。

 

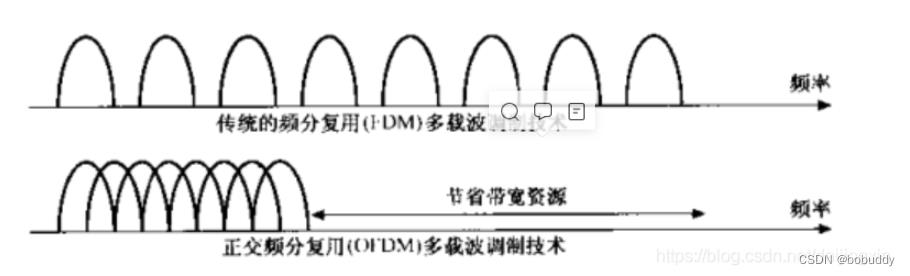
 图1.OFDM多载波调制技术示意图

1.OFDM的产生和发展
OFDM的思想早在20业纪60年代就已经提出,由于使用模拟滤波器实现起来的系统复杂度较高，所以一直没有发展起来。在20世纪70年代，S.B.Weinstein 提出用离散傅里叶变换(DFT)实现多裁波调制，为OFDM的实用化奠定了理论基础;在80年代，LJ.Cimini首先分析了OFDM在移动通信应用中存在的问题利解决方法,从此以后，OFDM在移动通信中的应用得到了迅猛的发展。

OFDM系统收发机的典型框图如下图所示。发送端将被传输的数字信号转换成子载波幅度和相位的映射,并进行离散傅里叶反变换(IDFT)将数据的频谱表达式变到时域上。IFFT变换与j IDFT变换的作用相同，只是有更高的计算效率，所以适用于所有的应用系统。其中，上半部分对应于发射机链路，下半部分对应于接收机链路。由于FFT操作类似于IFFT， 因此发射机和接收机可以使用同一硬件设备。当然，这种复杂性的节约则意味着该收发机不能同时进行发送和接收操作。

 

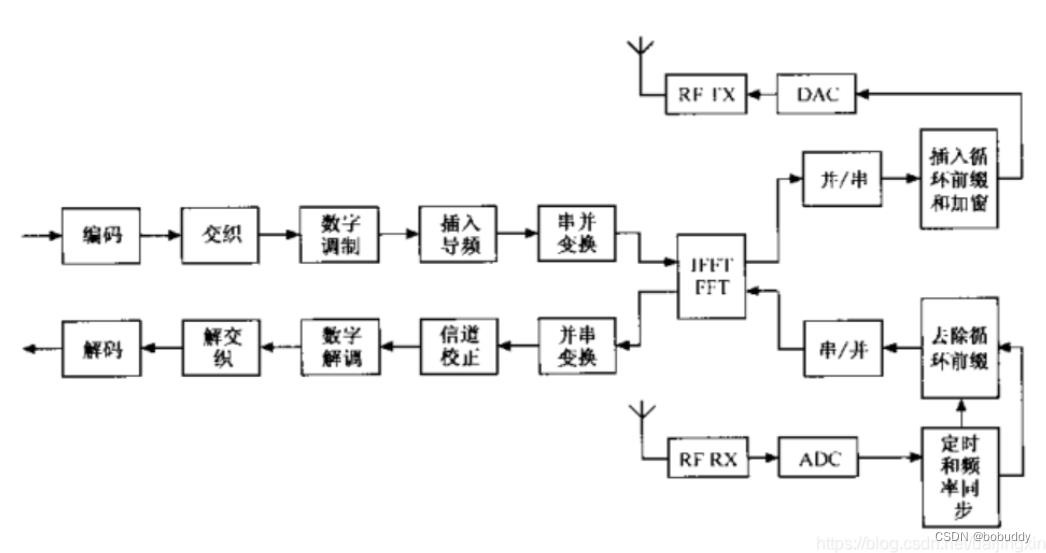
 图2.OFDM系统收发机框图
接收端进行发送端相反的操作，将射频信号（RF）信号与基带信号进行处理，并用FFT变换分解频域信号，子载波的幅度和相位被采集出来并转换回数字信号。

2.串并转换
数据传输的典型模式是串行数据流，数据被连续传输，每个数据都占据了整个可利用带宽。采用并行传输的方式则减少在串行系统中出现的问题。

在OFDM系统中，每个符号的传输速率在几十bit/s到几十kbits/s之间，所以必须进行串并转换，将串行比特流数据转化为可传输的OFDM信号。在发送端进行完调制后，在接收端进行相反的过程，从各个子载波处来的数据转换回原始的串行数据。

当一个OFDM符号在多径无线信道中传输时频率选择性衰落会使几组子载波受到很大的衰减引起比特错误。因此为了提高性能，大多数系统采用数据加扰作为串并转换工作的一部分。在接收端进行逆过程解出信号，不仅能还原出原数据比特原来的顺序，同时还可以分散由于信道衰落引起的连串比特错误并使其在时间上近似均匀分布，使系统的性能得到改进。

    表1.单载波和多载波传输方式的比较

 

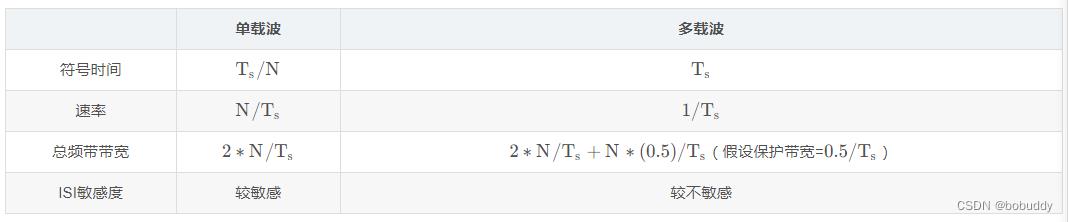
3.子载波调制

一个OFDM符号之内包含多个经过相移键控（PSK）或者正交幅度调制（QAM）的子载波。

一旦要把传输的比特分配到各个子载波上，某一种调制模式则将他们映射为子载波的幅度和相位，通常采用等效基带信号来描述OFDM的输出信号：

 

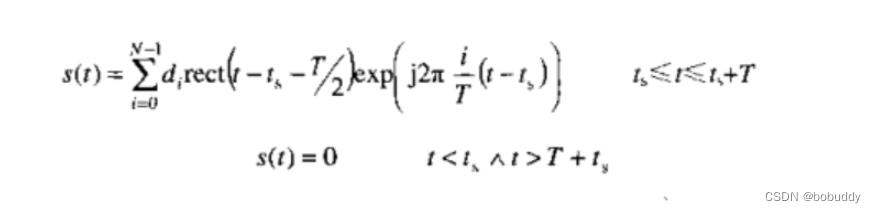
其中信号的实部和虚部分别对应OFDM的同相和正交分量，在实际系统可以分别与对应的c o s coscos分量和s i n sinsin分量相乘。

 

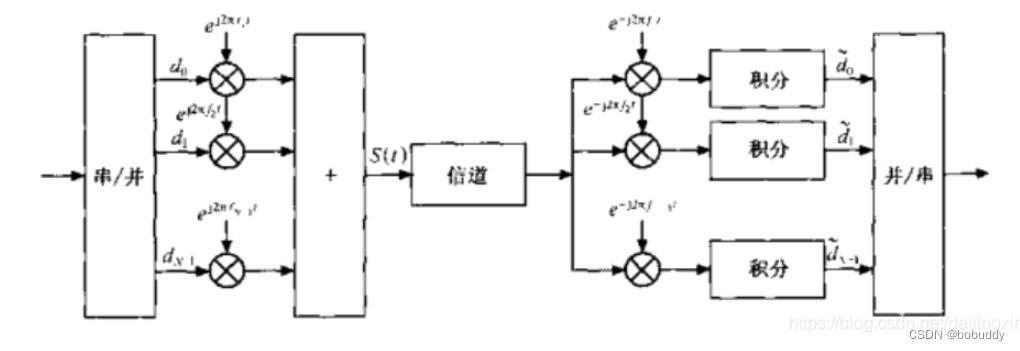
 图3.调制操作示意图

在实际的应用中根据数据符号的调制方式，每个子载波的幅度和相位各不相同，每个子载波在一个OFDM信号周期中都有多个周期，并且各个相邻的子载波相差一个周期，这也是子载波存在正交性的原因。

 

 图4.OFDM调制子载波示意图

这种正交性还可以从频域角度来解释。每个OFDM符号在其周期T内包括多个非零的子载波。因此其频谱可以看作是周期为T TT的矩形脉冲的频增与一组位于各个子载波频率上的δ函数的卷积。矩形脉冲的频谱幅值为s i n c ( f T ) sinc(fT)sinc(fT)函数， 这种所数的零点出现在频率为1 / T 1/T1/T整数倍的位置上。这种现象可以参见图5，图中给出了相互覆盖的各个子信道内经过矩波形成型得到的符号的s i n c sincsinc函数频谱。在每个子载波频率最大值处，所有其他子信道的频谱值恰好为零。因为在对OFDM符号进行解调的过程中，需要计算这些点上所对应的每个子载波频率的最大值，所以可以从多个相关重叠的子信道符号中提取每一个子信道符号，而不会收到其它子信道的干扰。

 

 图5.OFDM子载波频谱示意图

不难看出，OFDM符号频域可以满足奈奎斯特采样定理，多个子信道频谱之间不存在相互干扰。因此这种当一个子信道频谱为最大而其它为0的情况能够避免ICI。

 

4.DFT的实现
傅里叶变换将时域与频域联系在一起。通常使用快速傅里叶变换（FFT）。
对于子载波数比较多的系统，OFDM的复等效基带信号可以采用离散傅里叶逆变换的方式来实现：

 

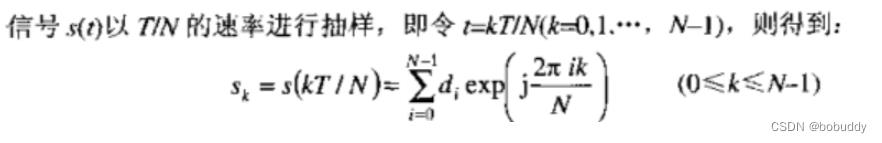
在接收端为了恢复出原始的数据信号，进行离散傅里叶变换：

 

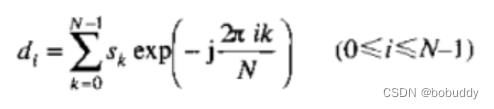
因此我们可以看出OFDM系统的调制和解调可以用IDFT和DFT来代替。通过N点的IDFT运算，把频域数据转换为时域数据，经过射频载波调制之后，发送到无线通道中。其中每个IDFT输出的数据符号都是由所有的子载波信号叠加生成的，即对多个经过调制的子载波叠加信号进行抽样得到。

在实际使用中，通常采用更加方便快捷的IFFT/FFT。

5.保护间隔、循环前缀和子载波数的选择
应用OFDM的一个重要原因在于它可以有效地对抗多径时延扩展。把输入数据流中并变换到N NN个并行的子信道中，使得每一个调制子载波的数据周期可以扩大为原始数据符号周期的N NN倍，因此时延扩展与符号周期的数值比也同样降低N NN倍。为了最大限度的消除符号间干扰，还可以在每个OFDM符号之间插入保护间隔(GI, Guard Interval)，而且该保护间隔长度一般要大于无线信道中的最大时延扩展，这样一个符号的多径分量就不会对下一 个符号造成干扰。在这段保护间隔内可以不插任何信号，即是一段空白的传输时段。然而在这种情况下，由于多径传播的影响，会产生载波间干扰(ICI)，即子载波之间的正交性遭到破坏，不同的子载波之间会产生干扰。这种效应如下图所示。每个OFDM符号中都包括所有的非零子载波信号，而且也可同时出现该OFDM符号的时延信号，图中给出了第1子载波利第2 子载波的时延信号。从图中可以看到，由于在FFT运算时间长度内，第1子载波和第2子载波之间的周期个数之差不再是整数，所以当接收机试图对第1子载波进行解调时，第2子载波会对第1子载波造成干扰。同样，当接收机对第2子载波进行解调时，也会存在来自第1子载波的干扰。

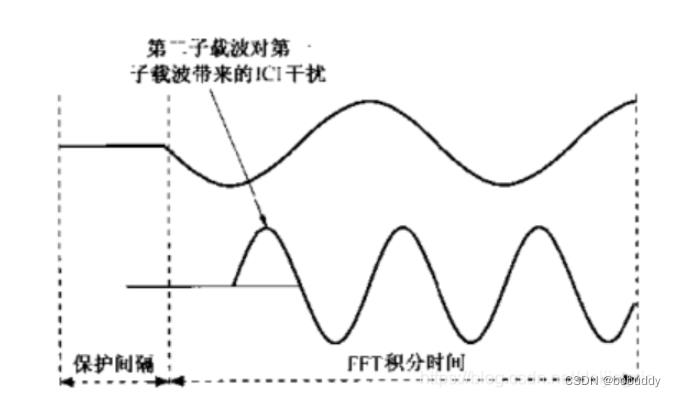
 图6.ICI干扰示意图

在系统带宽和数据传输速率都给定的情况下OFDM信号的符号速率将远远低于单载波的传输模式。例如在单载波BPSK调制模式下，符号速率就相于传输的比特速率，而在OFDM中，系统带宽被N NN个子载波占用，符号速率则为单载波传输模式的1 / N 1/N1/N。正是因为这种低符号速率使OFDM系统可以自然地抵抗多径传播导致的符号间干扰(ISI)，另外，通过在每个符号的起始位置增加保护间隔可以进一步抵制ISI，还可以减少在接收端的定时偏移错误。这种保护间隔是一种循环复制，增加了符号的波形长度，在符号的数据部分，每个子载波内有一个整数倍的循环，此种符号的复制产生了一个循环的信号，即将每个OFDM符号的后T g T_gT g
​    
 时间中的样点复制到OFDM符号的前面形成前缀，因此交接点没有任何的间断。因此将一个符号的尾端复制并补允到起始点增加了符号时间的长度，下图显示了保护间隔的插入。

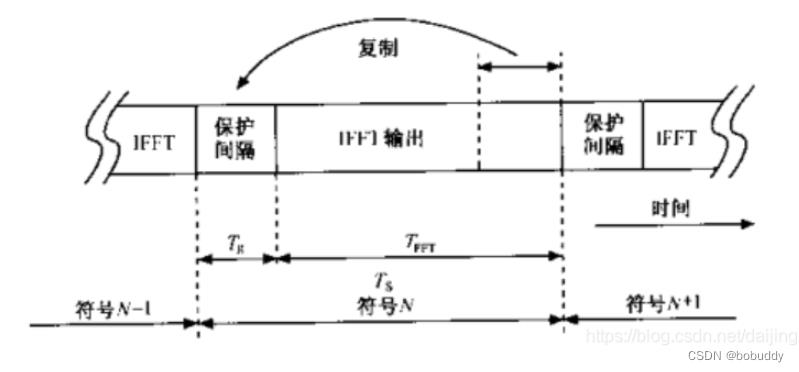
图7.插入保护间隔示意图

 

只有当保护间隔远远大于最大多径时延的时候才能克服ISI的影响。

增加OFDM符号的周期能减少ISI的影响，为了确定这种影响，定义了一种衡量标准：

其中，τ \\tauτ为延迟扩展，T TT为符号周期。在给定带宽的OFDM你号中，符号周期与子载波数日是成比例的。如果η ηη很大时，大量独立的OFDM符号受到ISI的影响，导致系统的高误比特率:相反，如果η ηη值很小，则只有一小部分的独立OFDM符号受到ISI的影响，因此系统的误比特率较低。

 

图8给出了3种不同子载波数条件下的16QAM星座图，其信源符号等概率地从16QAM星座点种进行选取，η ηη值分别为6.25%，3.125%和1.56%，η ηη值最小的对应于数量最大的子载波。图8表示，ISI相对于子载波数大的OFDM系统而言，对子载波数小地OFDM系统影响更大。

 

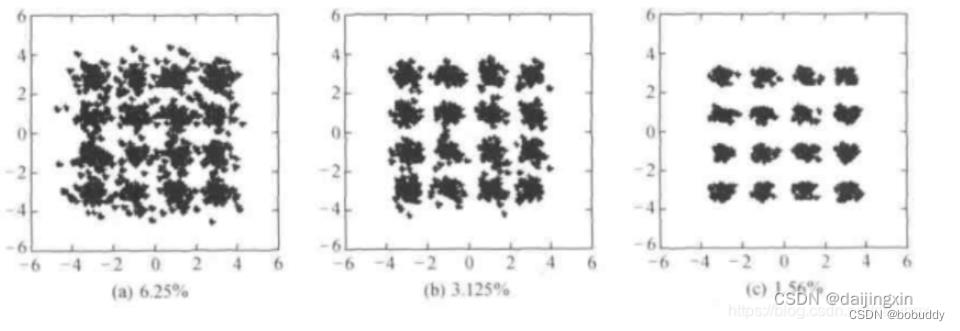
 图8.16QAM星座图

当加入保护间隔后会带来功率和信息速率的损失，功率损失可由下式表示：

 

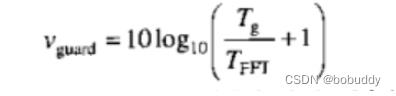
不难看出，即时保护间隔达到20%，功率损失也不过1db，但其速率损失高达20。由于插入保护间隔可以消除ISI和ICI，代价是值得的。

加入循环前缀还有一个作用就是，使每个OFDM符号的一部分呈现周期性，将信号与信道冲激响应的线性卷积转换成循环卷积，时域循环卷积相当于频域直接相乘，从而可以进行频域均衡。

 

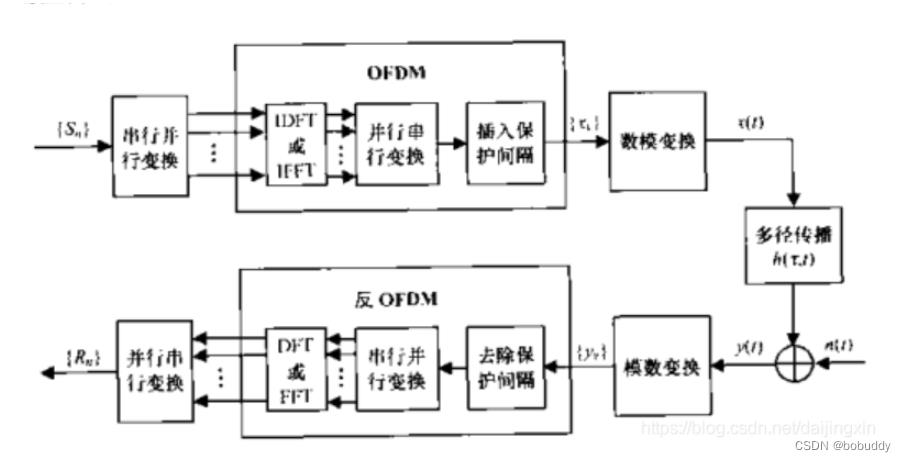
 图9.系统框图

通过适当的选择子载波的个数，能够使信道响应平坦，插入保护间隔还有利于保持子载波的正交性，因此OFDM有可能完全消除ISI和多径带来的ICI影响。

6.加窗技术

 图10.OFDM信号的功率谱密度示意图

 

根据OFDM符号的功率谱密度，其带外衰减比较慢，为了加快带外衰减的速度我们需要使用加窗技术。

通常采用升余弦类型的窗函数：

 

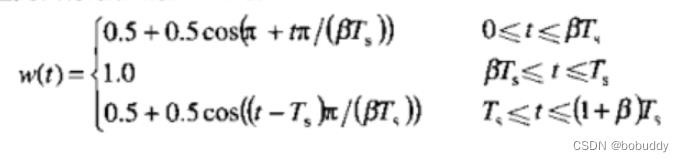
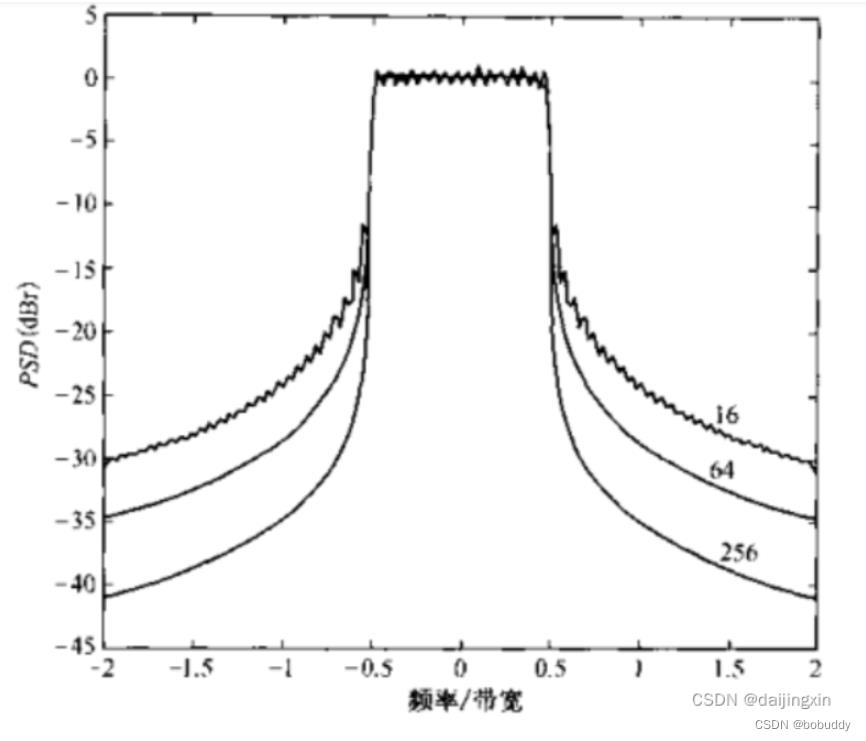
 图11.子载波个数分别为16、64和256的OFDM系统的PSD

 

 

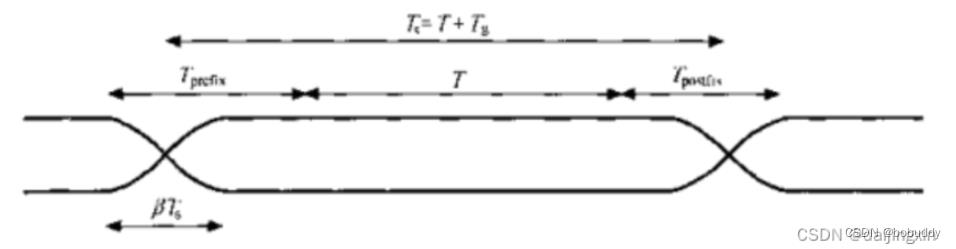
 图12.经过加窗处理后的OFDM符号示意图

下图给出在128个子载波的情况下，有不向滚降系数B的升余弦窗函数的OFDM符号的功率谱密度。可以看到，滚降系数为0.025的升余弦函数可以大大的降低带外辐射功率，而时域内由于滚降系数β ββ所造成的信号叠加只占符号周期的2.5%。从图中还可以得到，β ββ值越人,带外辐射功率下降的也就越快，但同时也会降低OFDM符号对时延扩展的容忍程度。例如，即使时延信号的时延长度没有超过保护间隔长度T g T_gT g
​    
 ，但由于滚降系数的存在，使得非恒定信号幅度部分有可能落入到FFT的时间长度T TT之内，又因为只有各个子载波的幅度以及相位在FFT周期T TT内保持恒定，才会保证子载波之间的正交性，所以滚降系数β ββ的存在可能带来ICI和ISI,使得保护间隔的有效长度由原米的T g TgTg减小到现在的β T s β TsβTs。

图13.滚降系数分别为0（矩形函数）、0.025、0.05、0.1和0.5的升余弦加窗函数对OFDM系统功率谱密度的影响

 

7.RF调制

OFDM调制器输出了一个基带信号，将此信号与所需传输频率进行混频操作需要通过混频器完成，可以采用模拟混频器或者数字混频器，由于数字调制技术提高了处理I、Q信道之间的匹配性和相位准确性，因此更加的精准。

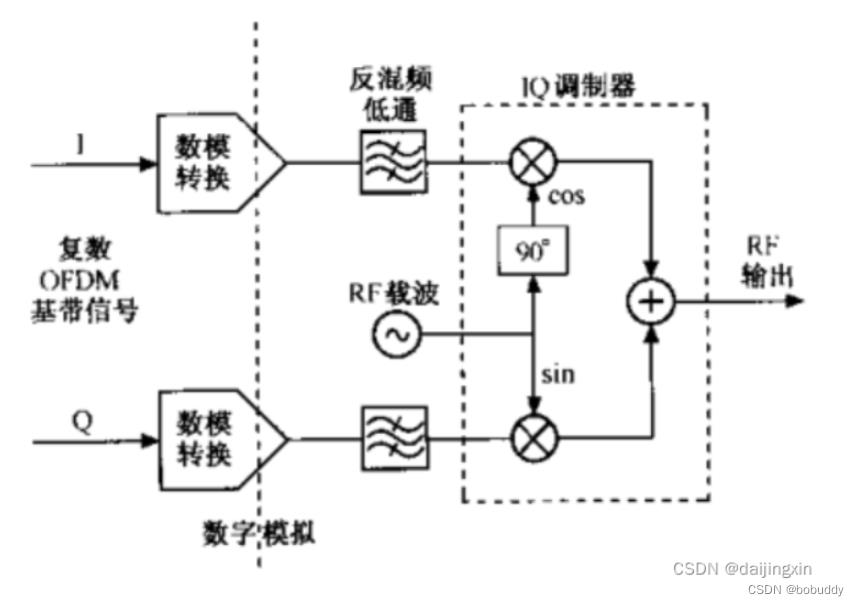
 图14.OFDM系统的模拟混频器

 

 图15.OFDM系统的数字混频器

8.OFDM基本参数的选择
各种OFDM参数的选择就是需要在多项要求冲突中进行折中考虑。通常来讲，首先要确定3个参数:带宽(Bandwidth)、比特率(Bit Rate)及保护间隔(Guard Interval),按照惯例,保护问隔的时间长度应该为应用移动环境信道的时延扩展均方根值的2~4倍。

一旦确定了保护问隔，则OFDM符号周期长度就可以确定。为了最大限度的臧少由于插入保护比特所带来的信噪比的损失，希望OFDM符号周期长度要远远大于保护间隔长度。但是符号周期长度又不可能任意大，否则OFDM系统中要包括更多的子载波数，从而导致子载波间隔相应减少，系统的实现复杂度增加，而且还加大了系统的峥值平均功率比，同时使系统对频率偏差更加敏感。因此在实际应用中，一般选择符号周期长度是保护间隔长度的5倍，这样由于插入保护比特所造成的信噪比损耗只有1dB左右。

在确定了符号周期和保护间隔之后,子载波的数量叮以直接利用3dB带宽除以子载波间隔(即去掉保护间隔之后的符号周期的倒数)得到。或者可以利用所要求的比特速率除以每个子信道的比特速率来确定子载波的数量。每个信道中所传输的比特速率可以由调制类型、编码速率和符号速率来确定。

原文链接：https://blog.csdn.net/daijingxin/article/details/108110436