双足轮机器人SK8O技术详解--控制系统翻译
Posted 灯哥开源
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了双足轮机器人SK8O技术详解--控制系统翻译相关的知识,希望对你有一定的参考价值。
3 控制系统
在本章中,我将介绍用于稳定和运动控制的控制器,状态观测器以及跳跃轨迹的计算。 基于线性化的3D轮式倒立摆模型,我设计了状态反馈控制律。为了过滤和融合所有可用的测量,我使用了无迹卡尔曼滤波器。最后,我通过求解非线性优化问题来描述跳跃状态轨迹的计算。
3.1 稳定与运动控制
最初,打算基于线性化的平面模型为机器人的左侧和右侧设计两个独立的LQ状态控制器。不幸的是,由于这种系统的非最小相位动力学,该方法在偏航运动中变得不稳定,因为未考虑两侧的耦合。通过引入一个外部比例偏航阻尼器,我设法在仿真中克服了这个问题。 当在实物机器人上应用时,该解决方案被证明是无效的,因为在仿真中起作用的阻尼器增益太大,从而导致真实机器人的抽搐和摔倒。另一方面,具有较小增益值的阻尼器无法稳定偏航动力学。因此,我必须使用包含偏航耦合器的模型来进行控制器设计。我自然选择了完整的机器人3D模型。然而,本文旨在为机器人的第一个原型设计一种控制系统。因此,我打算尽可能简化数学模型和控制系统。我决定使用机器人的倒立摆简化来实现轮子稳定和身体电机的PD控制,与[3]中类似。
3.1.1 非线性模型的平衡
在进行控制器设计之前,我需要找到机器人的配置-平衡-使机器人稳定。 由于导出的运动方程是非线性且复杂的,用解析的方法计算它的解将是一项乏味甚至不可能完成的任务。因此,我采用了数值优化。
我将平衡时的角加速度和速度设置为零,因此根据(2.27):

这与(2.31)中的降阶模型一起给出了平衡条件:

可以进一步简化为:

如果
g
g
g项是由输入
τ
i
n
τ_in
τin补偿的,或者如果向量
−
g
+
τ
i
n
-g + τ _in
−g+τin是
G
T
G^T
GT的零空间的元素,则满足条件。为了找到这样的平衡点,我制定了以下优化任务:

在条件(3.3)和闭环运动约束(2.15)的情况下,以指定的期望值
θ
1
θ_1
θ1来最小化输入力矩:

这个问题有多种解决方案。其中有一些会导致相交。为了避免这些配置,我限制了剩余角度的值,以使其位于可接受的范围内。我用Matlab中的约束非线性问题求解器找到了理想的解决方案,其结果如表3.1所示。
3.1.2 3D轮式倒立摆模型
大众熟知大多数的摆式系统模型,图3.1中所示的轮式摆也不例外。因此,我不必自己推导它,而使用文献[9]推导的那个模型。为了方便读者阅读,这里写出它的方程式。 状态空间模型如下:



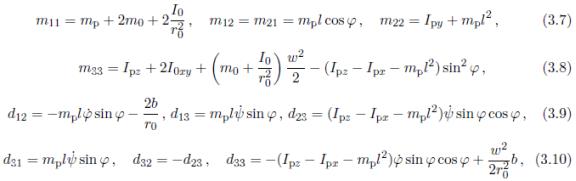
其中 I 0 x y I_0xy I0xy在垂直方向上轮子的转动惯量, m p m_p mp, I p x I_px Ipx, I p y I_py Ipy, I p z I_pz Ipz是不带轮子的整个摆的质量和转动惯量,l是连杆的长度, w w w是轮子的距离, x x x是摆的前进距离, φ \\varphi φ是俯仰角, ψ \\psi ψ是偏航角,并且 u 0 L u_0L u0L, u 0 R u_0R u0R分别是左右轮子的力矩。参数 m 0 m_0 m0, r 0 r_0 r0, I 0 I_0 I0, b b b, g g g与平面机器人模型中的参数相同。
接下来,使用上一部分的平面模型和平衡姿态来计算摆的参数。得到的摆的质量是除轮子以外的所有机器人零件质量的总和:
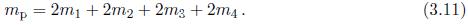
连杆长度l作为平衡位置下轮子与身体之间的距离来计算:

我决定忽略连杆的转动惯量,因为它们的值比身体的值小两个数量级。因此,我设置摆的惯性与Gazebo仿真器中的身体参数相匹配。距离
w
w
w也是根据3D Gazebo模型选择的。
3.1.3 线性化和离散化
接下来,继续进行3D轮式倒立摆模型的线性化(3.6):
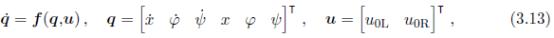
通过计算线性连续系统
A
c
A_c
Ac,
B
c
B_c
Bc的状态空间矩阵:
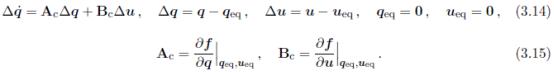
从线性连续系统中,我使用零阶保持器获得了状态空间矩阵
A
d
A_d
Ad,
B
d
B_d
Bd的离散时间系统:

其中
T
=
0.001
s
T = 0.001 s
T=0.001s是预期的采样周期。
3.1.4 控制器设计
有了线性化的模型之后,我进行了控制器的设计。首先,我通过消除偏航角和前进距离来简化模型。这些状态对稳定或操纵都不重要,其余状态均与它们无关。因此,减少仅仅关系到从 A d A_d Ad中删除第4行第4列和第6行第6列,以及从 B d B_d Bd中删除第4行和第6行。
获得简化模型的状态空间矩阵
A
r
A_r
Ar和
B
r
B_r
Br后,我创建了一个增强系统,在LQR中积分[10]以进行速度和偏航率的参考跟踪。

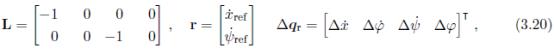
其中
ε
\\varepsilon
ε是积分跟踪误差,
I
I
I是2×2单位矩阵,
r
r
r是参考向量。然后遵循标准无限视野
L
Q
R
LQR
LQR设计程序[11],获得轮子稳定控制律的状态反馈增益
K
K
K和输入权重矩阵
Q
L
Q
R
Q_LQR
QLQR,
R
L
Q
R
R_LQR
RLQR:

反馈回路如图3.2所示。
摆的状态到已测量(或估计)的机器人状态的映射如下:
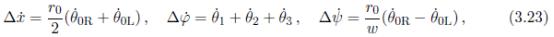

图3.2:建议的
L
Q
R
LQR
LQR的控制回路。

下标
R
R
R和
L
L
L表示机器人的右侧或左侧。
身体电机通过简单的
P
D
PD
PD控制律进行控制:
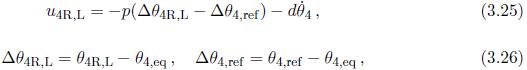
通过实验调整了
p
p
p,
d
d
d值。参考值用于更改机器人腿的长度,默认值为
Δ
4
,
r
e
f
=
0
\\Delta_4,ref = 0
Δ4,ref=0。
3.1.5 平衡性能
我检查了控制器对三个不同腿的长度值的平衡性能。第一个是由图2.2中的平衡值给出的默认长度。其他两种情况分别对应于图3.3中的拉伸和蹲坐机器人姿势,分别为 Δ 4 , r e f = 0.15 \\Delta_4,ref = 0.15 Δ4,ref=0.15 rad和 Δ 3 , r e f = − 0.15 \\Delta_3,ref = -0.15 Δ3,ref=−0.15 rad。
在测试场景中,我首先向静止的机器人背部施加了一个 2 k N 2 kN 2kN的 0.2 m s 0.2 ms 0.2ms长的冲击力,仿真了明显的向前推动。两秒钟后,我在机器人一侧施加了相同的冲击力,以查看身体控制器的性能。
系统的响应根据Gazebo仿真器的设置变化而发生变化,特别是约束力混合(CFM)参数值的变化。该参数用于通过将硬关节约束转换为软约束来提高仿真稳定性,从而降低精度。将CFM设置为较低的值或零时,在仿真过程中会出现关节角度和速度的峰值。另一方面,对于高的CFM值,仿真的行为是不自然的。我总是试图将CFM设置得尽可能低。在大多数仿真中,该值介于
1
0
3
10^3
103和
1
0
4
10^4
104之间。

在默认姿势下的机器人可以很好地处理两种干扰,如图3.4和3.5所示。后推力的力矩峰值,
u
0
u_0
u0是
−
0.7
N
m
-0.7 Nm
−0.7Nm,
u
4
u_4
u4是
0.4
N
m
0.4 Nm
0.4Nm。侧面碰撞后,
u
4
u_4
u4的峰值达到
±
0.5
N
m
±0.5 Nm
±0.5Nm,并且轮子上几乎没有施加力矩。侧面推动后,见到的振动是由机器人双腿之间的重量负载转移引起的。

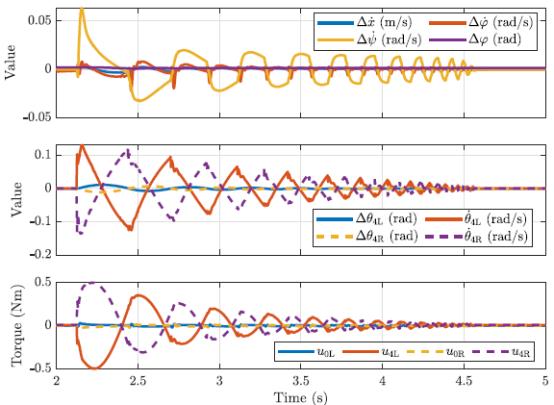
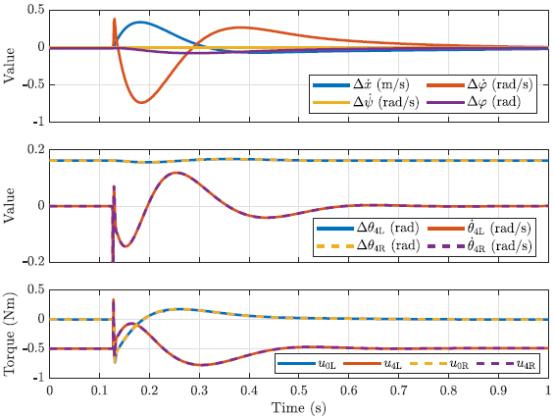
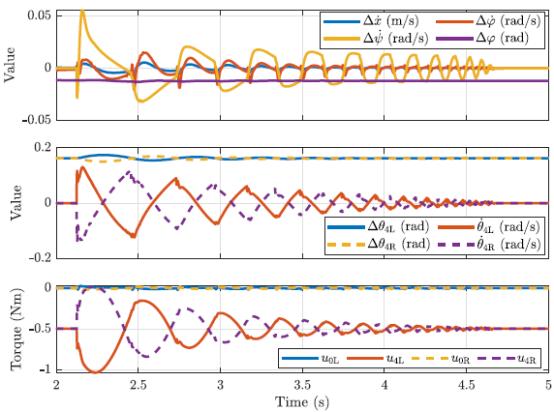
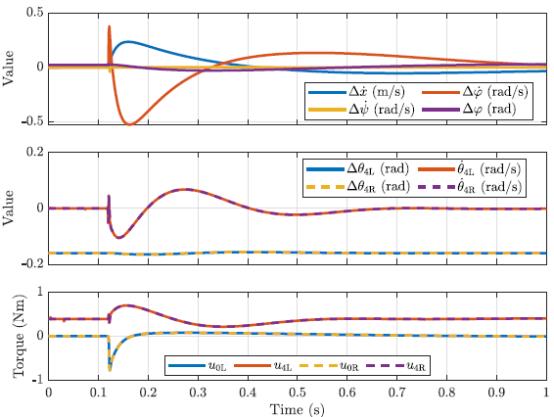
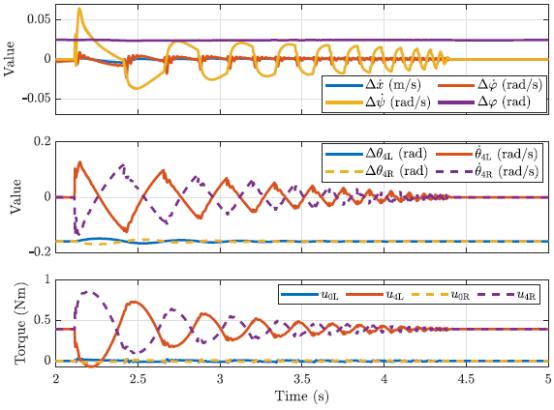
拉伸机器人的动作与默认姿势相似,如图3.6和3.7所示。唯一的例外是向后推动后立即出现 u 4 u_4 u4峰值,这可能是由与CFM参数相关的数值误差引起的。 u 4 u_4 u4和 Δ φ \\Delta_\\varphi Δφ的非零稳态值只是非平衡姿态稳定的结果。对于后推, u 0 u_0 u0再次在约 − 0.7 N m -0.7 Nm −0.7Nm处达到峰值,而 u 4 u_4 u4在与稳态值相差 ± 0.4 N m ±0.4 Nm ±0.4N以上是关于双足轮机器人SK8O技术详解--控制系统翻译的主要内容,如果未能解决你的问题,请参考以下文章