基于SVM的糖尿病数据集回归问题
Posted ZHW_AI课题组
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于SVM的糖尿病数据集回归问题相关的知识,希望对你有一定的参考价值。
目录
1. 作者介绍
谢蓉蓉,女,西安工程大学电子信息学院,2021级研究生
研究方向:图像处理
电子邮件:443369505@qq.com
吴燕子,女,西安工程大学电子信息学院,2021级研究生,张宏伟人工智能课题组
研究方向:人工智能与模式识别
电子邮件:1219428323@qq.com
2. SVM算法介绍
2.1 支持向量机分类
1、线性可分支持向量机:
给定线性可分的训练数据集,通过(硬)间隔最大化或者等价的求解相应的凸二次规划问题学习得到的分离超平面为:
以及相应的分类决策函数: 。
2、线性支持向量机
给定线性不可分的训练数据集,通过软件间隔最大化或者等价的求解相应的凸二次规划问题学习得到的分离超平面为:
以及相应的分类决策函数: 。
3、非线性支持向量机
从非线性分类训练集,通过核函数与软间隔最大化,或者凸二次优化,学习得到的分类决策函数
其中, 是正定核函数。
2.2 支持向量回归模型
SVM(Support Vector Machine)又称为支持向量机,最初是一种二分类的模型,后来修改之后也是可以用于多类别问题的分类。支持向量机可以分为线性核非线性两大类。其主要思想为找到空间中的一个更够将所有数据样本划开的超平面,并且使得数据集中所有数据到这个超平面的距离最短。支持向量也可以用于回归,此时叫支持向量回归(Support Vector Regression,简称SVR)。
回归就像是寻找一堆数据的内在的关系。不论这堆数据有几种类别组成,得到一个公式,拟合这些数据,当给个新的坐标值时,能够求得一个新的值。所以对于SVR,就是求得一个面或者一个函数,可以把所有数据拟合了(就是指所有的数据点,不管属于哪一类,数据点到这个面或者函数的距离最近)
统计上的理解就是:使得所有的数据的类内方差最小,把所有的类的数据看作是一个类。
传统的回归方法当且仅当回归f(x)完全等于y时才认为是预测正确,需计算其损失;而支持向量回归(SVR)则认为只要是f(x)与y偏离程度不要太大,既可认为预测正确,不用计算损失。具体的就是设置一个阈值α,只是计算 |f(x) - y| > α 的数据点的loss。支持向量回归表示只要在虚线内部的值都可认为是预测正确,只要计算虚线外部的值的损失即可。
支持向量回归模型(Support Vector Regression,SVR)是使用SVM来拟合曲线,做回归分析。与分类的输出是有限个离散的值不同的是,回归模型的输出在一定范围内是连续的。与SVM是使用一个条带来进行分类一样,SVR也是使用一个条带来拟合数据。这个条带的宽度可以自己设置,利用参数ϵ来控制。有一点和SVM是正好相反的:SVR希望样本点都落在“隔离带”内,而SVM希望样本点都在“隔离带”外。如图:

2.3 核函数和损失函数
在SVM/SVR中,如果没有核映射思想的引入,那么SVM/SVR就是一种加了距离限制的PLA(感知机)
准确的来说,核函数在机器学习中更应该是一种技巧,这种技巧主要体现在不需要明确的指定核映射的具体形式。核映射一般有三总情况:1.在不增减维度的情况下做变换,2.涉及到维度的增减,3.两种情况都包含。
核函数一般有多项式核、高斯径向基核、指数径向基核、多隐层感知核、傅立叶级数核、样条核等,在回归模型中,不同的核函数对拟合的结果会有较大的影响。
针对于非线性支持向量回归机,通常做法就是将低维数据映射到高维的空间,在高维空间中找到线性可分的超平面,最后再把高维空间的超平面映射回低维空间,这样就可以实现SVM的分类或者SVR的回归。但是,将低维的数据映射到高维的空间,在高维空间做计算,计算量特别大,尤其是当维度很高的情况下,而且也会容易过拟合。
核函数就是为了解决这个问题产生的,用核函数代替线性方程中的线性项可以使原来的线性算法非线性化,即能做非线性回归,此时引进核函数达到了升维的目的,也可以有效的控制过拟合。通俗的讲就是应用核函数就是在低维时就对数据做了计算,这个计算可以看做是将低维空间的数据映射到高维空间中做的计算(就是一个隐式变换)。
除核函数外,还有一个比较重要的概念就是损失函数:
损失函数是学习模型在学习过程中对误差的一种度量,一般在模型学习前已经选定,不同的学习问题对应的损失函数也不同,同一学习问题选取的损失函数不同得到的模型也会不同。
在SVR中对于损失函数构成的模型,有些权重很大,有些权重很小,这样就会容易导致过拟合(就是过分拟合了训练数据集),而过拟合则是因为样本太多的特征被包含进来,很多与项目本身无关的特征也被包含进来。
解决过拟合问题有很多方式,常见的有以下几种:
1)喂数据,也就是给足够多的数据,只有数据多了,数据的很多特征才会更加明显的体现出来,训练的模型也会不断的修正,特征的作用也会体现的越来越大。
2)特征降维,越多的特征导致训练集的维度越高,降维就是把高维空间的数据投影到低维空间中(保存下来的特征是数据量大的)。主要有:PCA降维(主成分分析,无监督)、反向特征消除、随机森林/组合树、LDA(线性判别分析,有监督)、LLE(局部线性嵌入)、Laplacian Eigenmaps(拉普拉斯特征映射)等
3)针对具体的负荷预测,对电量值进行标准化或者归一化。可以时特征训练集能够快速的收敛,可以使特征值域范围变小,有利于提高精度。
2.4 SVR模型的代价函数
在SVM模型中边界上的点以及两条边界内部违反margin的点被当做支持向量,并且在后续的预测中起作用;在SVR模型中边界上的点以及两条边界以外的点被当做支持向量,在预测中起作用。按照对偶形式的表示,最终的模型是所有训练样本的线性组合,其他不是支持向量的点的权重为0。
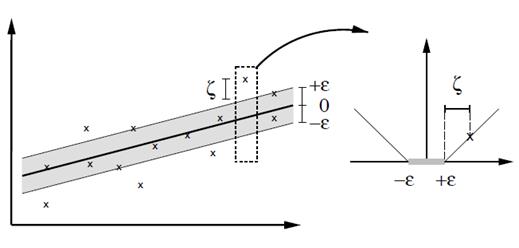
在margin内部的这些点的error都为0,只有超出了margin的点才会计算error。因此SVR的任务就是利用一条固定宽度的条带(宽度由参数ϵ来控制)覆盖尽可能多的样本点,从而使得总误差尽可能的小。
3. 实验过程
3.1 数据集介绍
糖尿病数据集:共442个样本,每个样本有十个特征,分别是 [‘age’, ‘sex’, ‘bmi’, ‘bp’, ‘s1’, ‘s2’, ‘s3’, ‘s4’, ‘s5’, ‘s6’],对应年龄、性别、体质指数、平均血压、S1~S6一年后疾病级数指标。
Targets为一年后患疾病的定量指标,值在25到346之间。适用于回归任务。

3.2 实验代码
################################
#第一步:导入相关模块
from sklearn.datasets import load_diabetes
# 导入数据集
import matplotlib.pyplot as plt
# 可视化
from sklearn.model_selection import train_test_split
# 导入数据集划分模块
from sklearn.preprocessing import StandardScaler
# 从sklearn.preprocessing导入数据标准化模块
from sklearn.svm import SVR
# 从sklearn.svm中导入支持向量机回归模型SVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
# 模型评估,使用R-squared、MSE、MAE指标评估
################################
#第二步:读取糖尿病数据集的数据并对糖尿病数据集的数据进行分割
diabetes = load_diabetes()
print(diabetes.DESCR)
x = diabetes.data
y = diabetes.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=33)
################################
#第三步:对训练数据和测试数据进行标准化处理
#分别初始化对特征值和目标值的标准化器
ss_x = StandardScaler()
ss_y = StandardScaler()
#训练数据都是数值型,所以要标准化处理
x_train = ss_x.fit_transform(x_train) ####标准化
x_test = ss_x.transform(x_test)
#目标数据也是数值型,所以也要标准化处理
y_train = ss_y.fit_transform(y_train.reshape(-1, 1))
y_test = ss_y.transform(y_test.reshape(-1, 1))
################################
#第四步:使用三种不同核函数配置的支持向量机回归模型进行训练,并且分别对测试数据进行预测
# 1.使用线性核函数配置的支持向量机进行回归训练并预测
linear_svr = SVR(kernel='linear')
linear_svr.fit(x_train, y_train.ravel())
linear_svr_predict = linear_svr.predict(x_test)
l1,=plt.plot(y_test, color='b', linewidth=2)
l2,=plt.plot(linear_svr_predict, color='r', linewidth=2)
plt.legend([l1,l2],['y_test','linear_svr_predict'],loc=2)
plt.show()
#2.使用多项式核函数配置的支持向量机进行回归训练并预测
poly_svr = SVR(kernel='poly')
poly_svr.fit(x_train, y_train.ravel())
poly_svr_predict = poly_svr.predict(x_test)
l1,=plt.plot(y_test, color='b', linewidth=2)
l2,=plt.plot(poly_svr_predict, color='r', linewidth=2)
plt.legend([l1,l2],['y_test','poly_svr_predict'],loc=2)
plt.show()
#3.使用径向基核函数配置的支持向量机进行回归训练并预测
rbf_svr = SVR(kernel='rbf')
rbf_svr.fit(x_train, y_train.ravel())
rbf_svr_predict = rbf_svr.predict(x_test)
l1,=plt.plot(y_test, color='b', linewidth=2)
l2,=plt.plot(rbf_svr_predict, color='r', linewidth=2)
plt.legend([l1,l2],['y_test','rbf_svr_predict'],loc=2)
plt.show()
################################
#第五步:对三种核函数配置下的支持向量机回归模型在相同测试集下进行性能评估
#1.线性核函数配置的SVR
print('The value of default measurement of linear SVR is', linear_svr.score(x_test, y_test))
print('R-squared value of linear SVR is', r2_score(y_test, linear_svr_predict))
print('The mean squared error of linear SVR is',mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_predict)))
print('The mean absolute error of linear SVR is',mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_predict)))
#2.多项式核函数配置的SVR
print('\\nThe value of default measurement of poly SVR is', poly_svr.score(x_test, y_test))
print('R-squared value of poly SVR is', r2_score(y_test, poly_svr_predict))
print('The mean squared error of poly SVR is',mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_predict)))
print('The mean absolute error of poly SVR is',mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_predict)))
#3.径向基核函数配置的SVR
print('\\nThe value of default measurement of rbf SVR is', rbf_svr.score(x_test, y_test))
print('R-squared value of rbf SVR is', r2_score(y_test, rbf_svr_predict))
print('The mean squared error of rbf SVR is',mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_predict)))
print('The mean absolute error of rbf SVR is',mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_predict)))
3.3 运行结果
线性核函数配置的支持向量机回归预测:
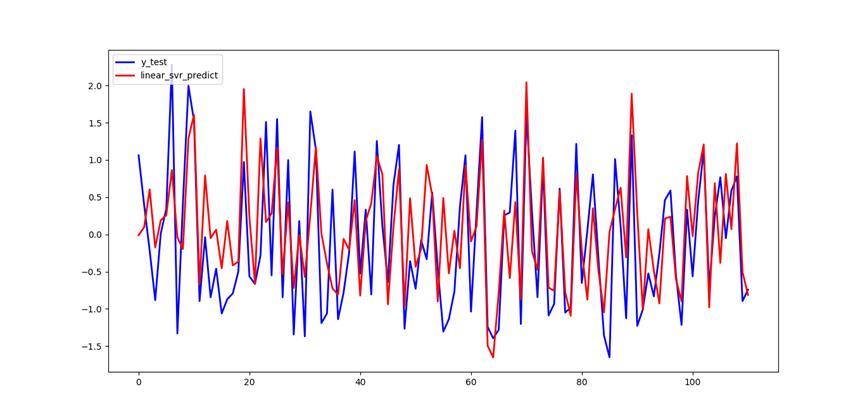
多项式核函数配置的支持向量机回归预测:
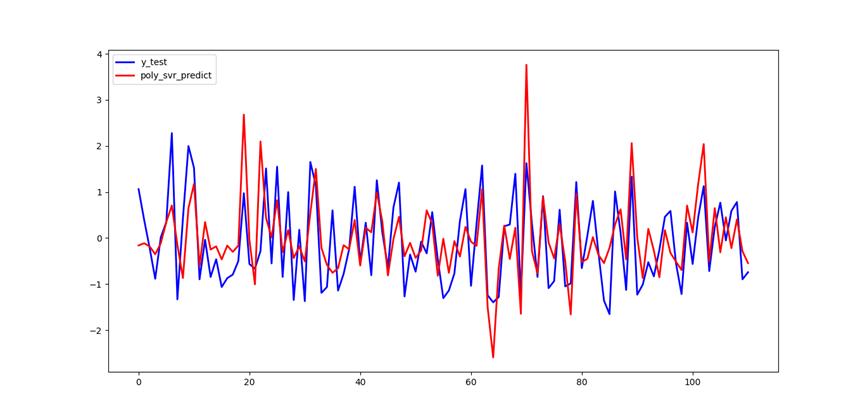
高斯核函数配置的支持向量机回归预测:

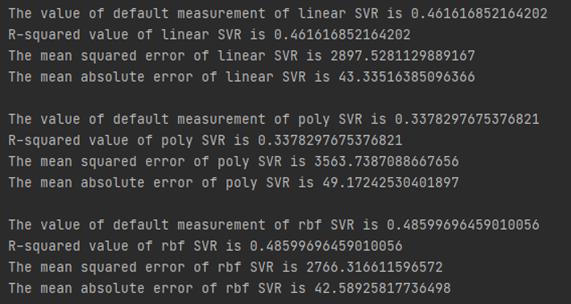
以上是关于基于SVM的糖尿病数据集回归问题的主要内容,如果未能解决你的问题,请参考以下文章