小米面试题看并查集

Posted 2022-12-02 刘二毛

首先，我们从一道题来引出这个问题。

假如已知有n个人和m对好友关系（存于数字r）。如果两个人是直接或间接的好友（好友的好友的好友…），则认为他们属于同一个朋友圈，请写程序求出这n个人里一共有多少个朋友圈。假如：n = 5，m = 3，r = 1 , 2 , 2 , 3 , 4 , 5，表示有5个人，1和2是好友，2和3是好友，4和5是好友，则1、2、3属于一个朋友圈，4、5属于另一个朋友圈，结果为2个朋友圈。

这道题解决它的办法就是利用并查集。

并查集是一种简单的集合，它支持 Union（把第二个子集合并入第一个集合）。注意只有两个集合不相交的时候才能并集。然后是Find，它用来搜索集合所给元素所在集合，然后返回集合的名字。

实现并查集：并查集的实现可以理解成森林。每一个集合是一棵树。在这里我们用可以用一个数组来表示，元素对应数组的下标，而根节点的内容我们认为都是-1。所以，默认的整个数组数值都为-1。所以我们初始化就是：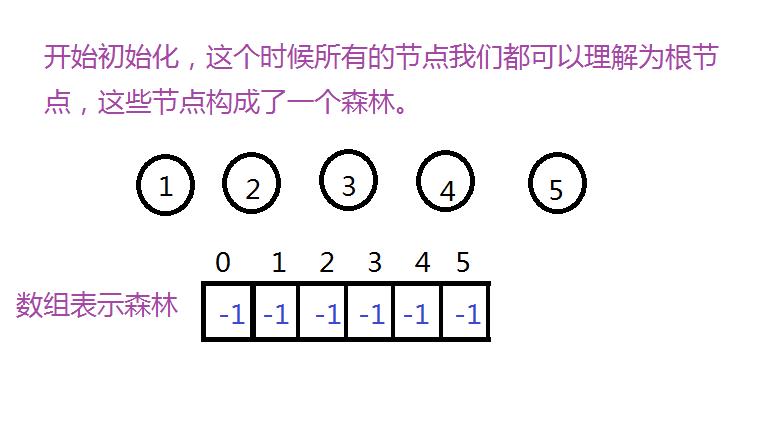 

当初始化完以后，我们就进行合并操作来解决。然后我们进行Union的操作。

Union（root1，root2）是把root2作为子集并入root1中，简单说就是找出root2的这棵树，并入root1，操作也就是把root2的根连到root1的根下。 
所以，在这里我们要并的时候，首先要找root1和root2的根，然后找到根以后，对它们的根进行并的操作。 
我们就拿上面那道题作为例子来画图说明。

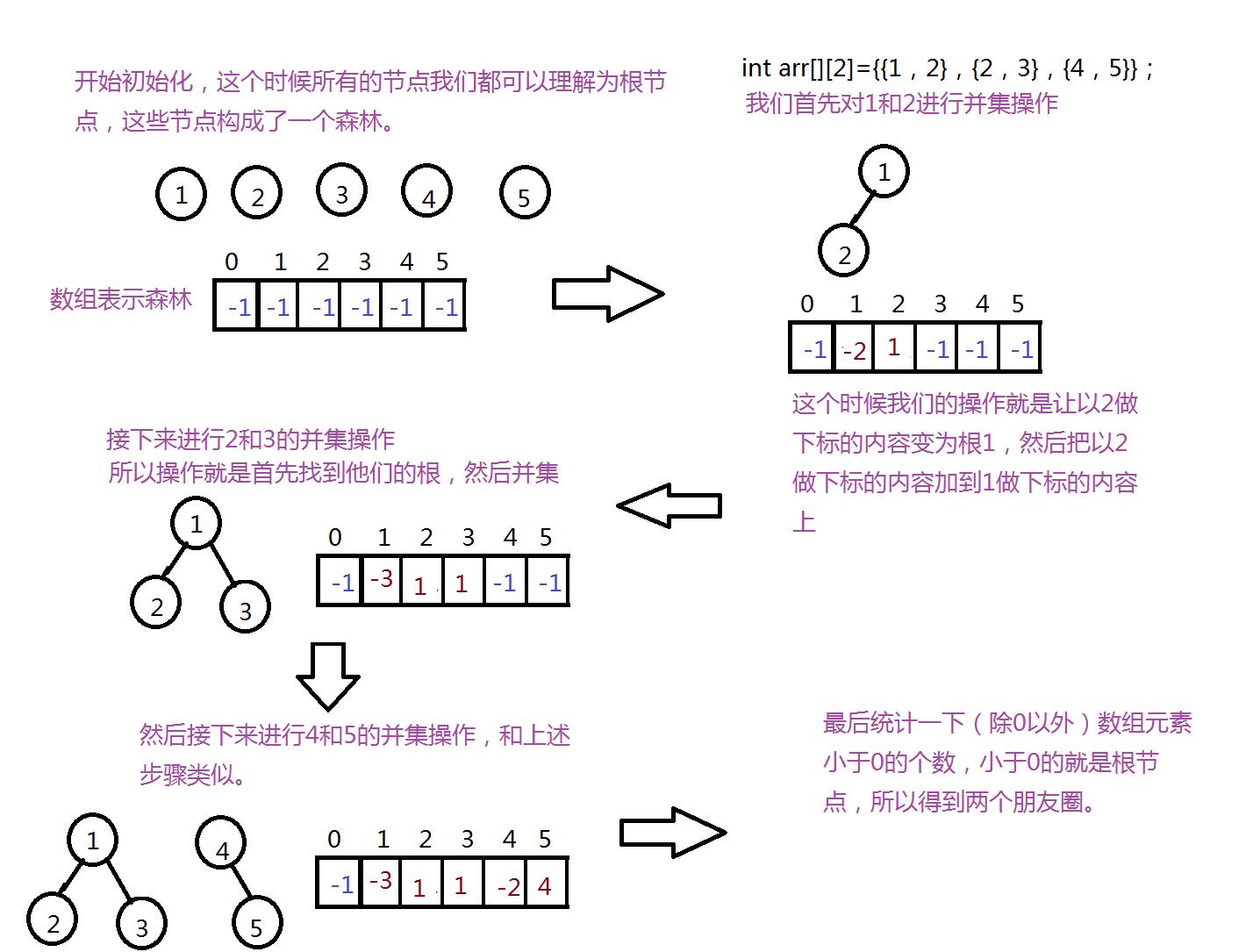
代码实现：

class UnionSet

public:
    UnionSet(int n)
        :_size(n + 1)
    
        //开辟一个数组，这个数组全为-1，因为是-1.所以使用memset就可以了，否则，考虑for循环
        _parent = new int[n + 1];
        memset(_parent, -1, sizeof(int)*(n + 1));

    
    ~UnionSet()
    
        delete[] _parent;
    
    //合并并查集
    void Union(int r1, int r2)
    
        //得到两个并查集的根
        int root1 = Find(r1);
        int root2 = Find(r2);
        //把第二个并查集加到第一个上，把父节点放到内容。
        if (root1 != root2)
        
            _parent[root1] += _parent[root2];
            _parent[root2] = root1;
        
    
    int Find(int index)
    
        int root = index;
        while (_parent[root] >= 0)
        
            root = _parent[root];
        
        return root;
    

    int CountRoot()
    
        int count = 0;
        for (int i = 1; i < _size; i++)
        
            if (_parent[i] <0)
                count++;
        
        return count;
    
protected:
    int *_parent;
    int _size;
;
int friends(int n, int m, int arr[][2])

    UnionSet a(n);
    for (int i = 0; i < m; i++)
    
        a.Union(arr[i][0], arr[i][1]);
    
    int rootcount = a.CountRoot();
    return rootcount;

void test1()

    int n = 3;
    int m = 5;
    int arr[][2] =   1, 2 ,  2, 3 ,  4, 5  ;

    int count = friends(n,m, arr);