编译原理笔记--词法分析

Posted 2022-12-02 FANCY PANDA

词法分析

正则表达式：L=aa,b * (ε∪(.,_a,ba,b * ))

正则表达式定义

• ε是一个RE，L(ε) = ε
• 如果 a∈∑，则a是一个RE，L(a) = a
• 假设 r和 s都是 RE，表示的语言分别是 L®和L(s)，则
• • r|s 是一个RE，L( r|s ) = L( r )∪L(s)
• • rs 是一个RE，L( rs ) = L( r ) L(s)
• • r* 是一个RE，L( r* )= (L( r ))*
• • ® 是一个RE，L( ( r ) ) = L( r )
    注：运算的优先级：*、连接、|

列题：
令 ∑ = a, b，则

 - L(a|b) = L(a)∪L(b) =a∪b = a, b
 - L((a|b)(a|b)) = L(a|b) L(a|b)=a, ba, b=  aa, ab, ba, bb  
 - L(a*) = (L(a))*= a*=  ε, a, aa, aaa, . . . 
 - L((a|b)*) = (L(a|b))* = a, b*=  ε, a, b, aa, ab, ba, bb, aaa, . . .
 - L(a|a*b) =  a, b, ab, aab, aaab, . . .

正则语言RE：

定律	描述
r｜s = s｜r	｜是可以交换的
r｜（ s｜t ）=（r｜s ）｜t	｜是可结合的
r（s t ）=（ r s ）t	连接是可结合的
r（s｜t ）= r s｜r t ; （s｜t ）r = sr｜t r	连接对｜是可分配的
εr = rε = r	ε 是连接的单位元
r * = （ r｜ε ) *	闭包中一定包含 ε
r **= r *	* 具有幂等性

正则定义：

正则定义是具有如下形式的定义序列：
d1→r1
d2→r2
…
dn→rn
其中：

• 每个di都是一个新符号，它们都不在字母表 Σ中，而且各不相同
• 每个ri是字母表 Σ∪d1 ,d2 , … ,di-1上的正则表达式

列题：
C语言中标识符的正则定义
  digit → 0|1|2|…|9
  letter_ → A|B|…|Z|a|b|…|z|_
  id → letter_(letter_|digit)*

有穷自动机FA

FA的典型例子

• 电梯控制装置

• 输入：顾客的乘梯需求（所要到达的层号）

• 状态：电梯所处的层数+运动方向

• 电梯控制装置并不需要记住先前全部的服务要求，只需要知道电梯当前所处的状态以及还没有满足的所有服务请求
  FA模型
  

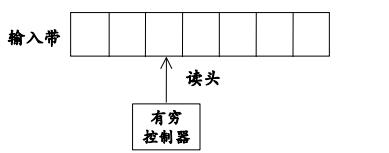
• 输入带(input tape)：用来存放输入符号串

• 读头(head )：从左向右逐个读取输入符号，不能修改（只）、不能往返移动

• 有穷控制器( finite control )：具有有穷个状态数，根据当前的状态和当前输入符号控制转入下一状态
  FA的表示

• 转换图 (Transition Graph)

• 结点：FA的状态

• 初始状态（开始状态）：只有一个，由start箭头指向

• 终止状态（接收状态）：可以有多个，用双圈表示

• 带标记的有向边：如果对于输入a，存在一个从状态p到状态q的转换，就在p、q之间画一条有向边，并标记上a
  
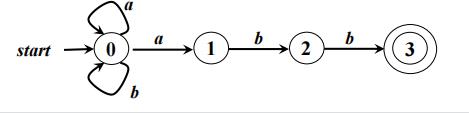
  FA定义（接收）的语言

• 给定输入串x，如果存在一个对应于串x的从初始状态到某个终止状态的转换序列，则称串x被该FA接收

• 由一个有穷自动机M接收的所有串构成的集合称为是该FA定义（或接收）的语言，记为L(M )
  
  最长子串匹配原则

• 当输入串的多个前缀与一个或多个模式匹配时，总是选择最长的前缀进行匹配

• 在到达某个终态之后，只要输入带上还有符号，DFA就继续前进，以便寻找尽可能长的匹配
  

DFA

M = ( S，Σ ，δ，s0，F )

• S：有穷状态集
• Σ：输入字母表，即输入符号集合。假设ε不是 Σ中的元素
• δ：将S×Σ映射到S的转换函数。 s∈S, a∈Σ, δ(s,a)表示从状态s出发，沿着标记为a的边所能到达的状态
• s0：开始状态 (或初始状态)，s0∈ S
• F：接收状态（或终止状态）集合，F⊆ S

例子：
一个DFA：M = ( S，Σ ，δ，s0，F )

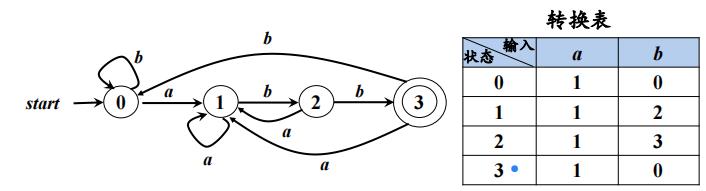
NFA

M = ( S，Σ ，δ，s0，F )

• S：有穷状态集
• Σ：输入符号集合，即输入字母表。假设ε 不是Σ中的元素
• δ：将S×Σ映射到2S的转换函数。s∈S, a∈Σ, δ(s,a)表示从状态s出发，沿着标记为a的边所能到达的状态集合
• s0：开始状态 (或初始状态)，s0∈ S
• F：接收状态（或终止状态）集合，F⊆ S
  例子：
  一个NFA：M = ( S，Σ ，δ，s0，F )
  

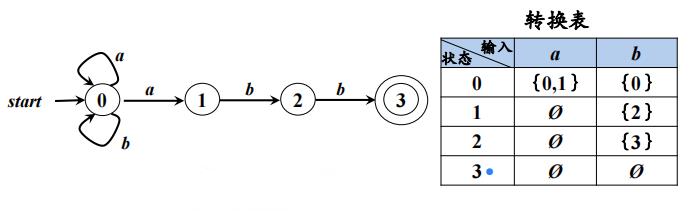
根据RE 构造NFA

例子:
r=(a|b) *abb 对应的NFA

列子：
从NFA到DFA的转换

列子：
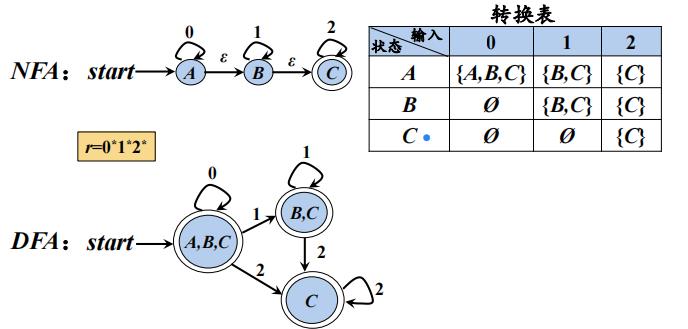
从带有ε-边的NFA到DFA的转换