数据结构与算法:树红黑树

Posted 2022-12-02 史大拿

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构与算法:树红黑树相关的知识，希望对你有一定的参考价值。

Tips: 采用java语言,关注博主,底部附有完整代码

工具:IDEA

本系列介绍的是数据结构: 树

这是第十一篇目前计划一共有11篇:

敬请期待吧~~

tips: 上一篇:2-3树,2-3-4树必须看!,因为红黑树就是为了解决2-3树,2-3-4树构建过于复杂产生的!

前言

红黑树(Red Bblack Tree), 看到这3字应该很熟悉又很陌生

熟悉是因为在很多地方都听到过他的大名,例如HashMap中等等

陌生是因为好像并没有了解过他,并不知道他是如何定义,如何运转的…

本篇就带大家从0到1,一点点分析,解刨,然后在 “组合” 起来

先来回顾一下上一篇的重点:

2-3树映射红黑树

2-3树转红黑树:

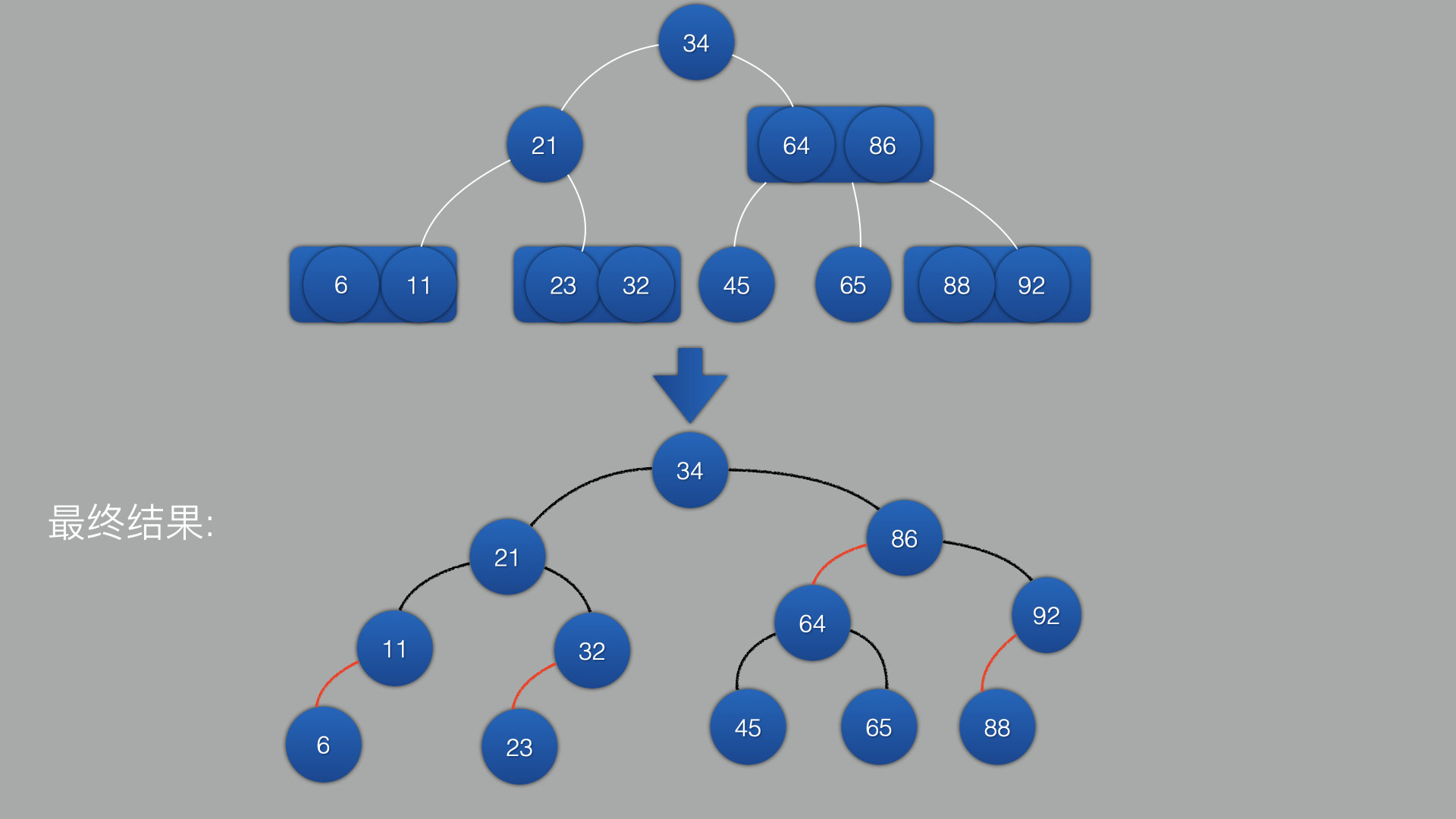
把线替换成具体的颜色:

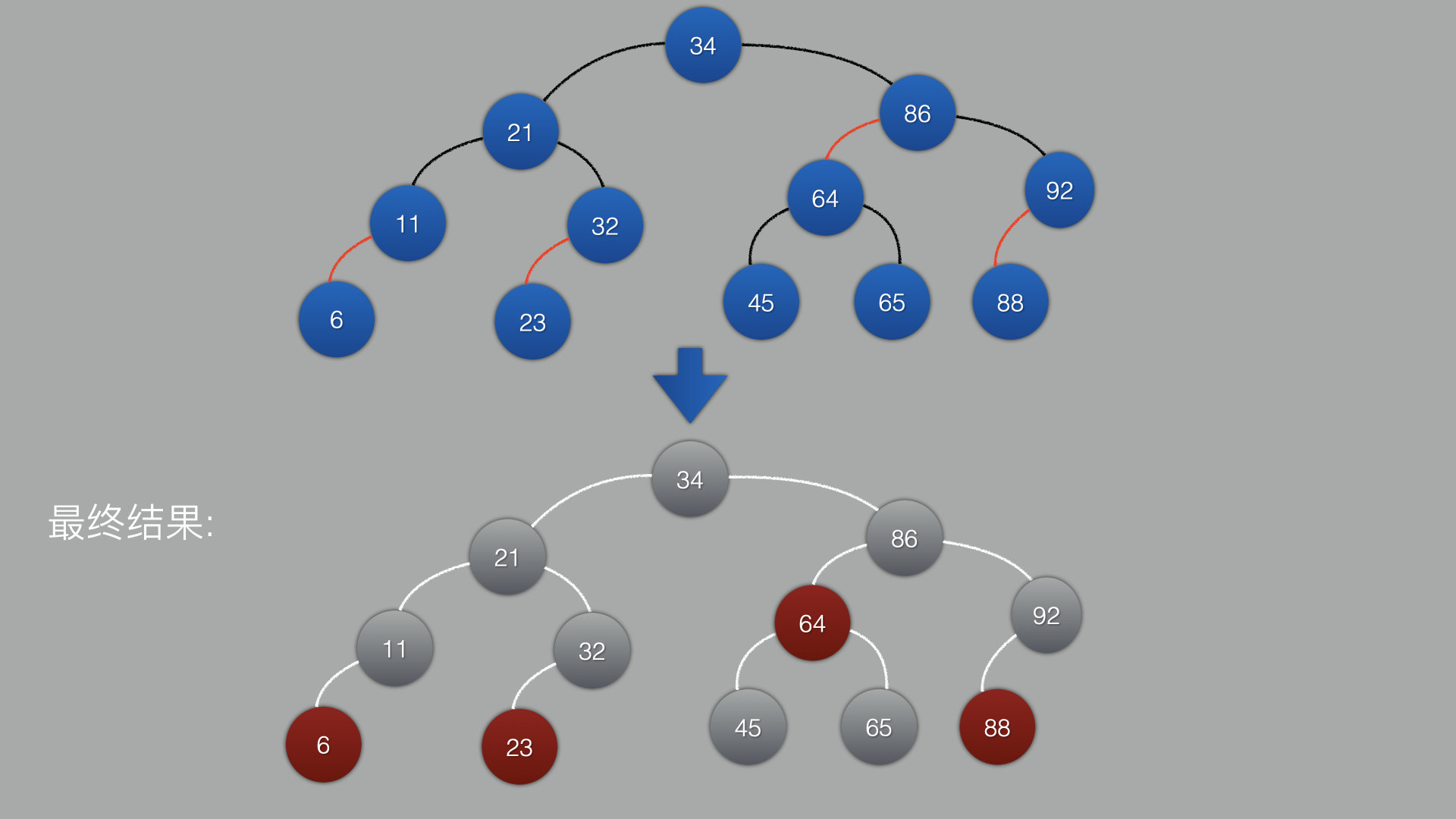
具体详细流程请去看上一篇

因为叶子结点也有左子/右子结点,只是叶子结点的左子/右子节点是null,如果他是null的话,默认是黑色

例如这样:

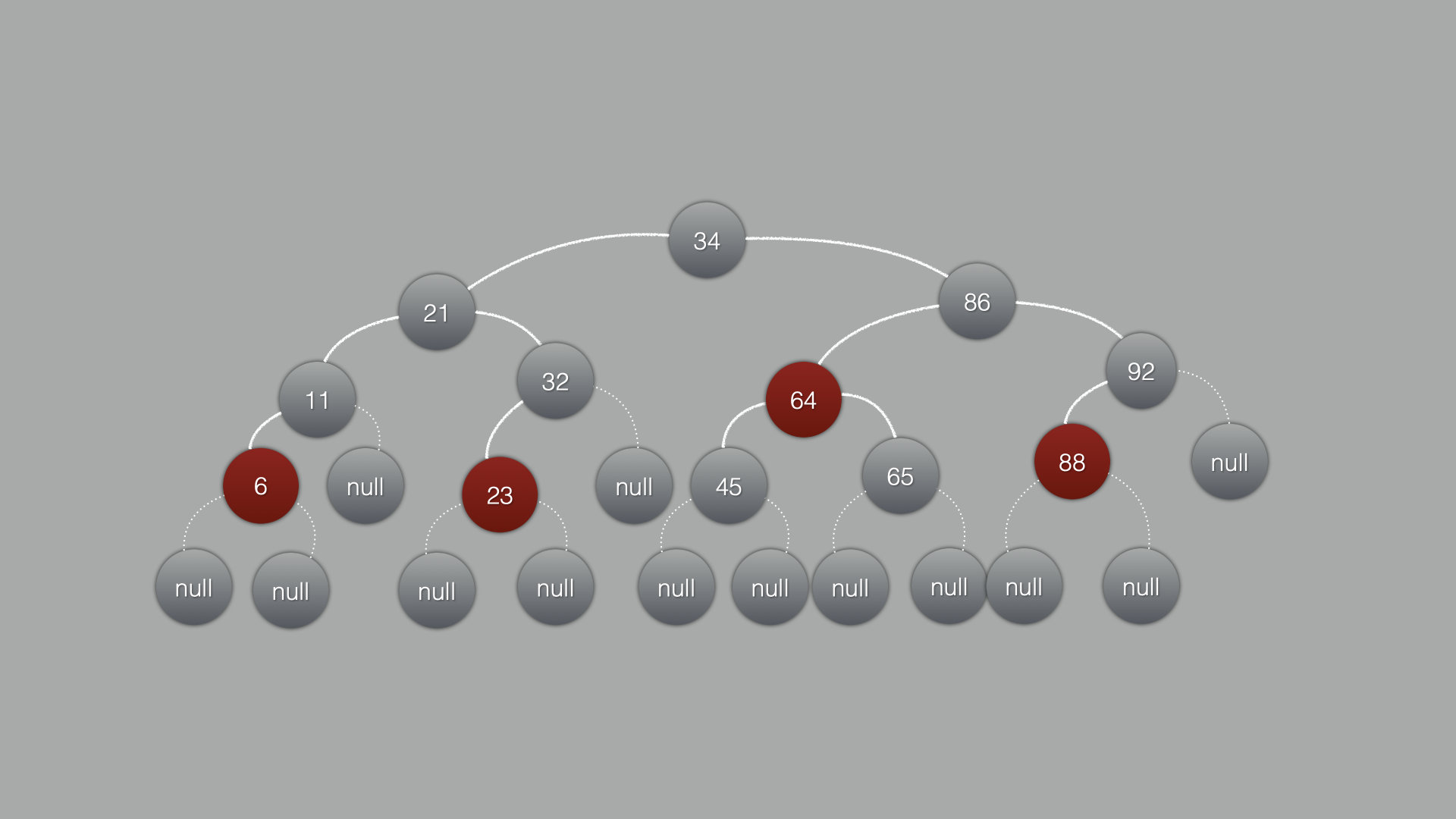
得出结论:最后一排默认都是黑色的

2-3-4树映射红黑树

2-3-4树转红黑树:

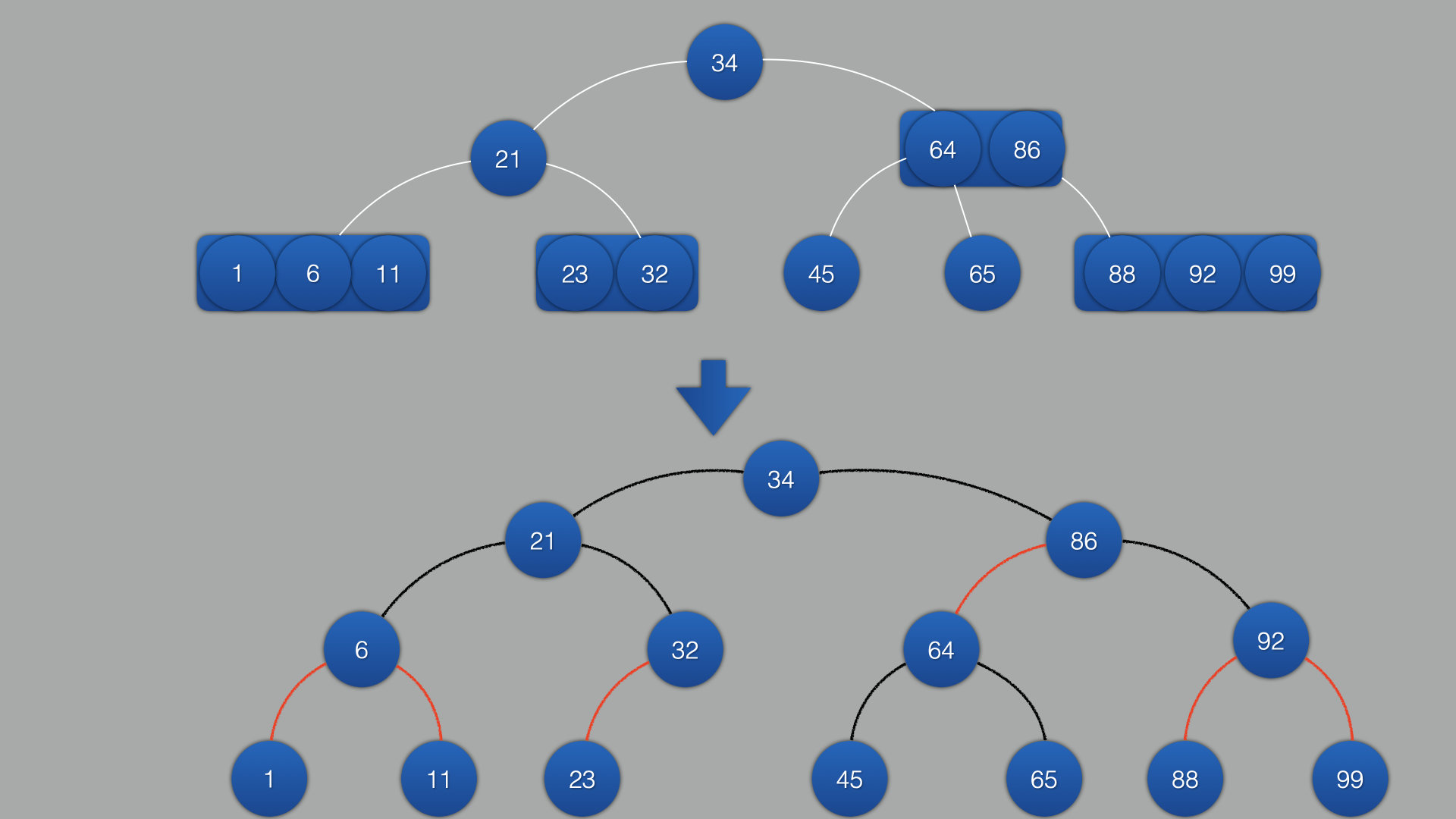
把线替换成具体的颜色:

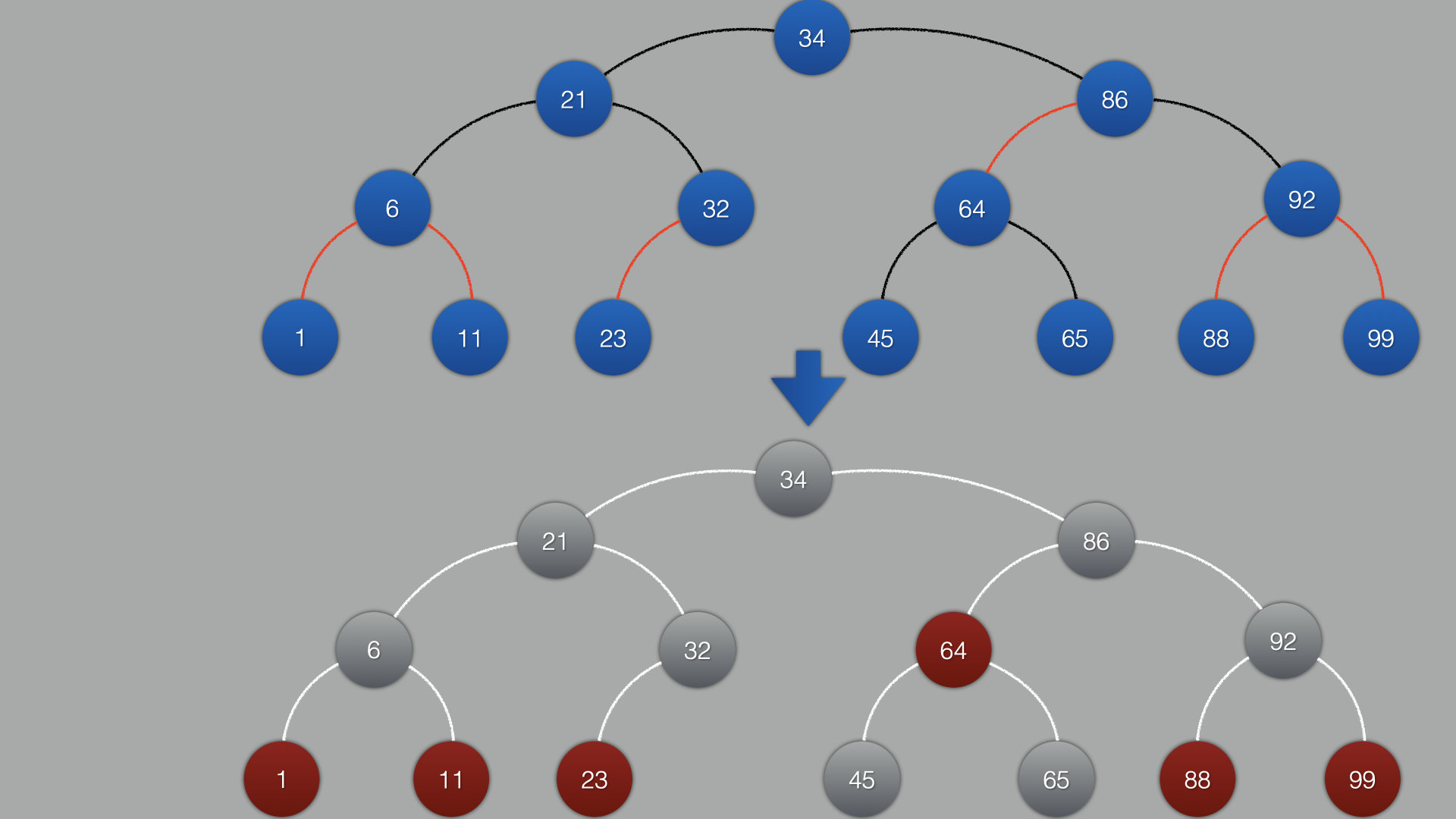
2-3树和2-3-4树得出的结论:

根结点一定是黑色
根结点到每个叶子结点的黑色结点个数相同 (所以有红黑树也叫黑色平衡树的说法)
不存在2个相邻的红色结点 (红色结点不能有子结点是红色的)
如果父结点是红色,那么他一定有一个黑色的爷爷结点
最后一排默认是黑色

角色分析

在红黑树中,有4个角色很重要

当前结点
父结点
叔叔结点
爷爷结点

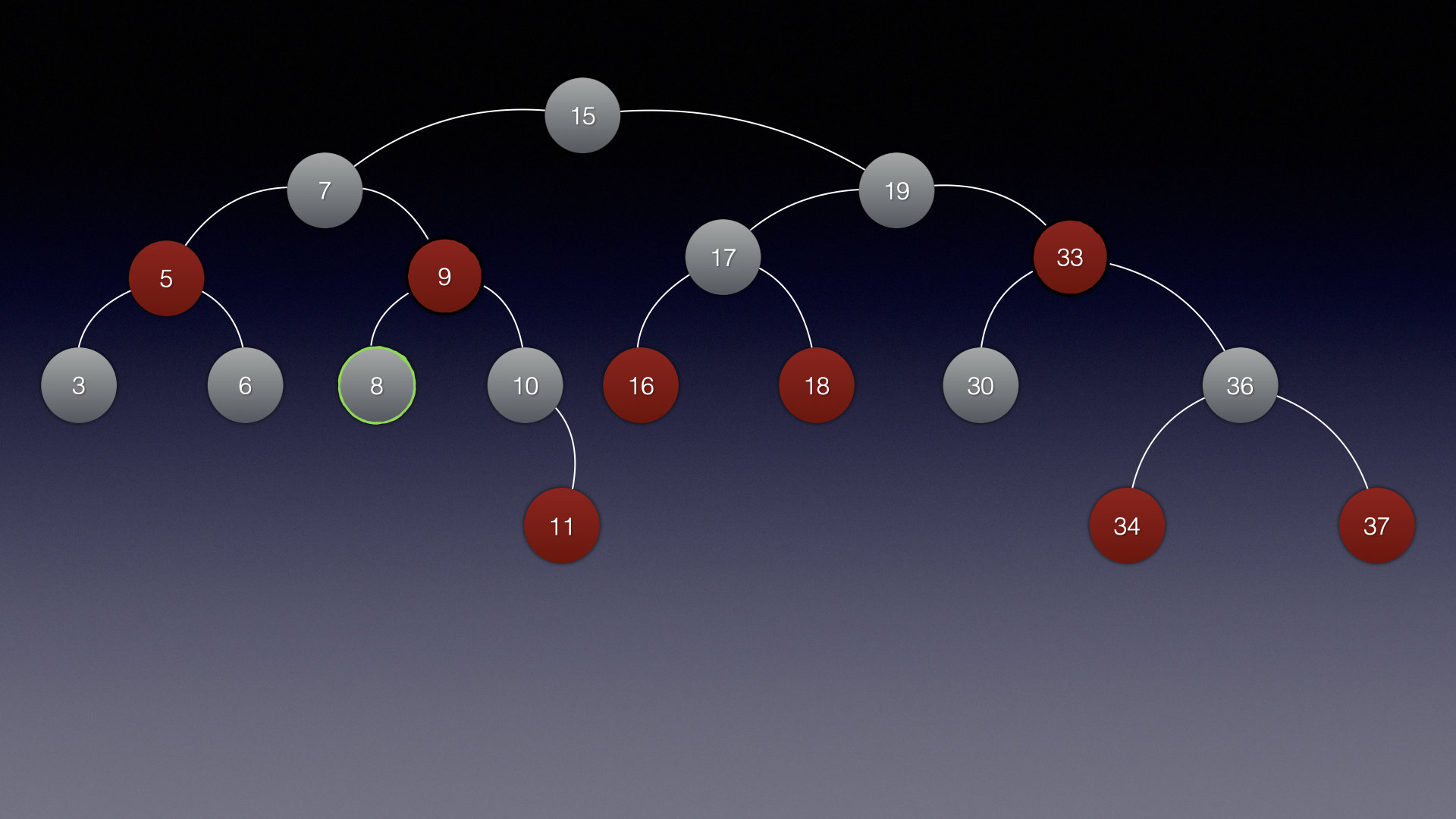
以这张红黑树图为例:

当前结点是 8
父结点是 9
叔叔结点是 5
爷爷结点是 7

清楚了这4个结点后,事情就简单了!

还有一点,插入结点一定是红色的,因为红色的有可能不影响平衡,但是黑色一定会影响平衡

这里的平衡指: 根结点到每个叶子结点的黑色结点个数相同

来看看具体场景:

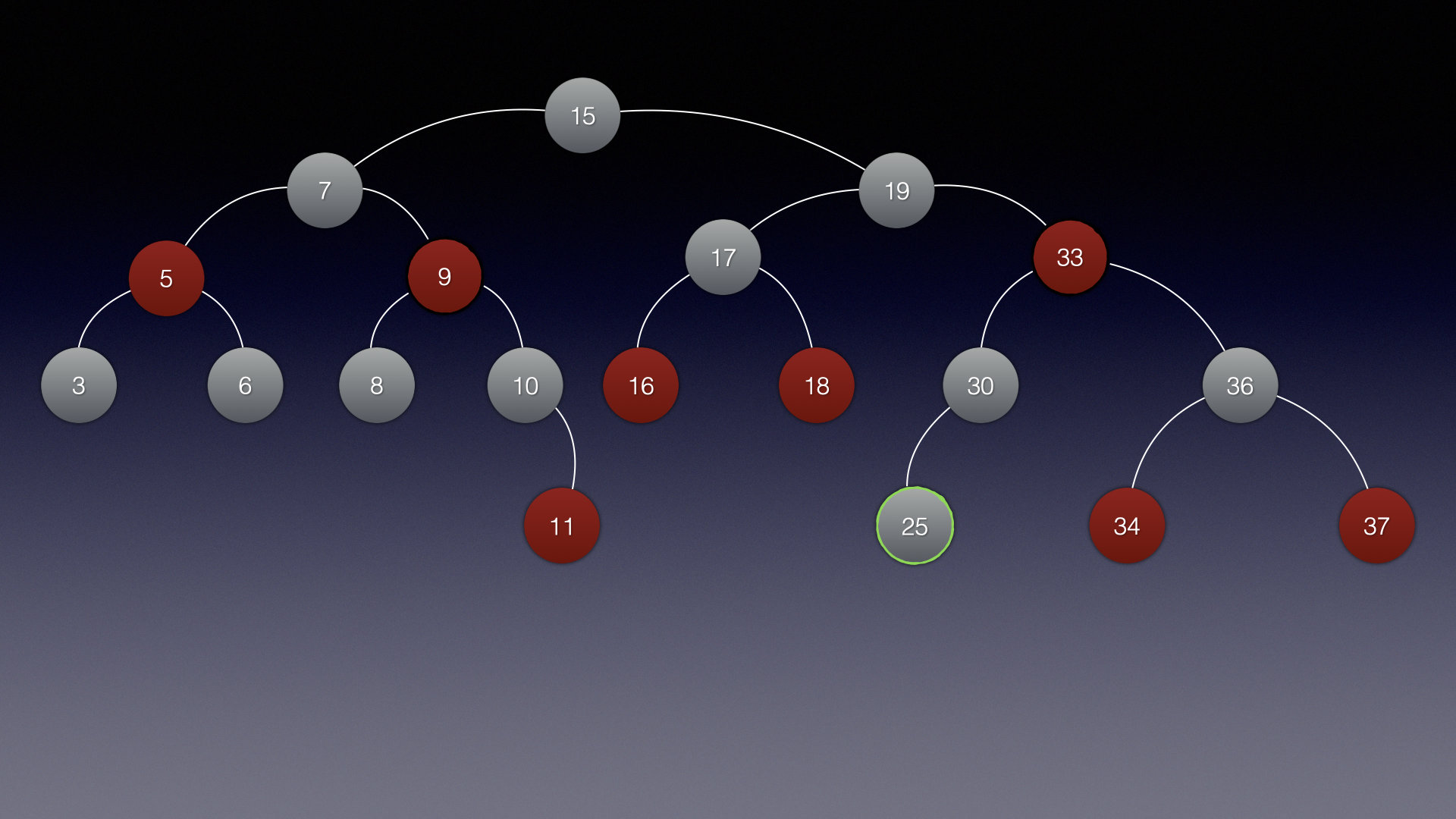
以插入25结点为例:

插入红色结点	插入黑色结点

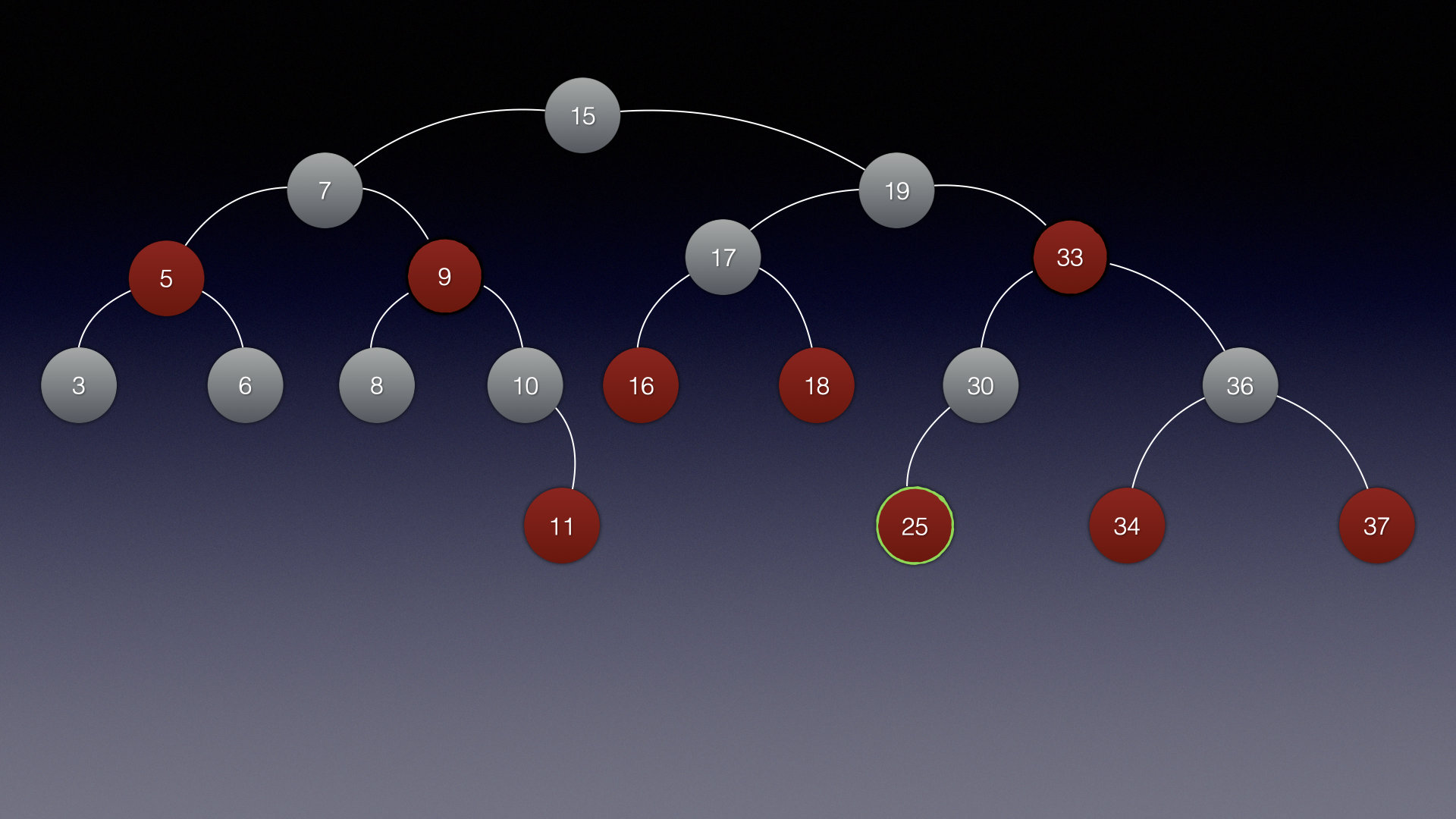可以看出插入红色结点并不影响平衡

但是插入黑色结点就违背了红黑树的原则 (根结点到每个叶子结点的黑色结点个数相同)

所以说,规定插入的结点都是红色

定义结点

public class RBTree 
     // 根节点
      private RBNode root;

      public RBTree(int rootValue) 
          this.root = new RBNode(null, null, BLACK, rootValue);
      
  
     /*
     * TODO 判断是否为红色
     */
    public boolean isRed(RBNode node) 
        if (node != null) 
            return node.color == RED;
        
        return BLACK;
    

    /*
     * TODO 判断是否为红色
     */
    public boolean isBlack(RBNode node) 
        if (node != null) 
            return node.color == BLACK;
        
        return BLACK;
    

    /*
     * TODO 设置颜色
     * @param color: [true 红色] [false黑色]
     */
    public void setColor(RBNode node, Boolean color) 
        if (node != null) 
            node.color = color;
        
    
  	
  	// 根结点
    public RBNode getRoot() 
          return root;
     
  
    // 中序遍历
  	public void show() 
        ....
    
  	
	  // 层序遍历
  	public void showFloor() 
    	  ....
    
  
  
    // 红黑结点
    public static class RBNode 
        // 左子结点
        public RBNode leftNode;

        // 右子结点
        public RBNode rightNode;

        // 结点颜色 [true 红色] [false黑色] 默认黑色
        public boolean color;

        // 父结点
        public RBNode parentNode;

        // 权值
        public int value;
        // 中序遍历
        public void show()  ...

api速看:

位置	名称	作用
RBTree.java	boolean isRed()	是否为红色
RBTree.java	boolean isBlack()	是否为黑色
RBTree.java	void setColor(RBNode,Boolean)	设置颜色 (true红色,false黑色)
RBTree.java	RBNode getRoot()	获取根结点
RBTree.java	void show()	中序遍历
RBTree.java	void showFloor()	层序遍历

旋转

红黑树的旋转道理和AVL树的旋转道理是相同的,但是代码写起来是不同的

因为红黑树有父结点的概念

AVL树并没有父结点的概念

在看具体步骤之前,先来定义好名字,方便调用

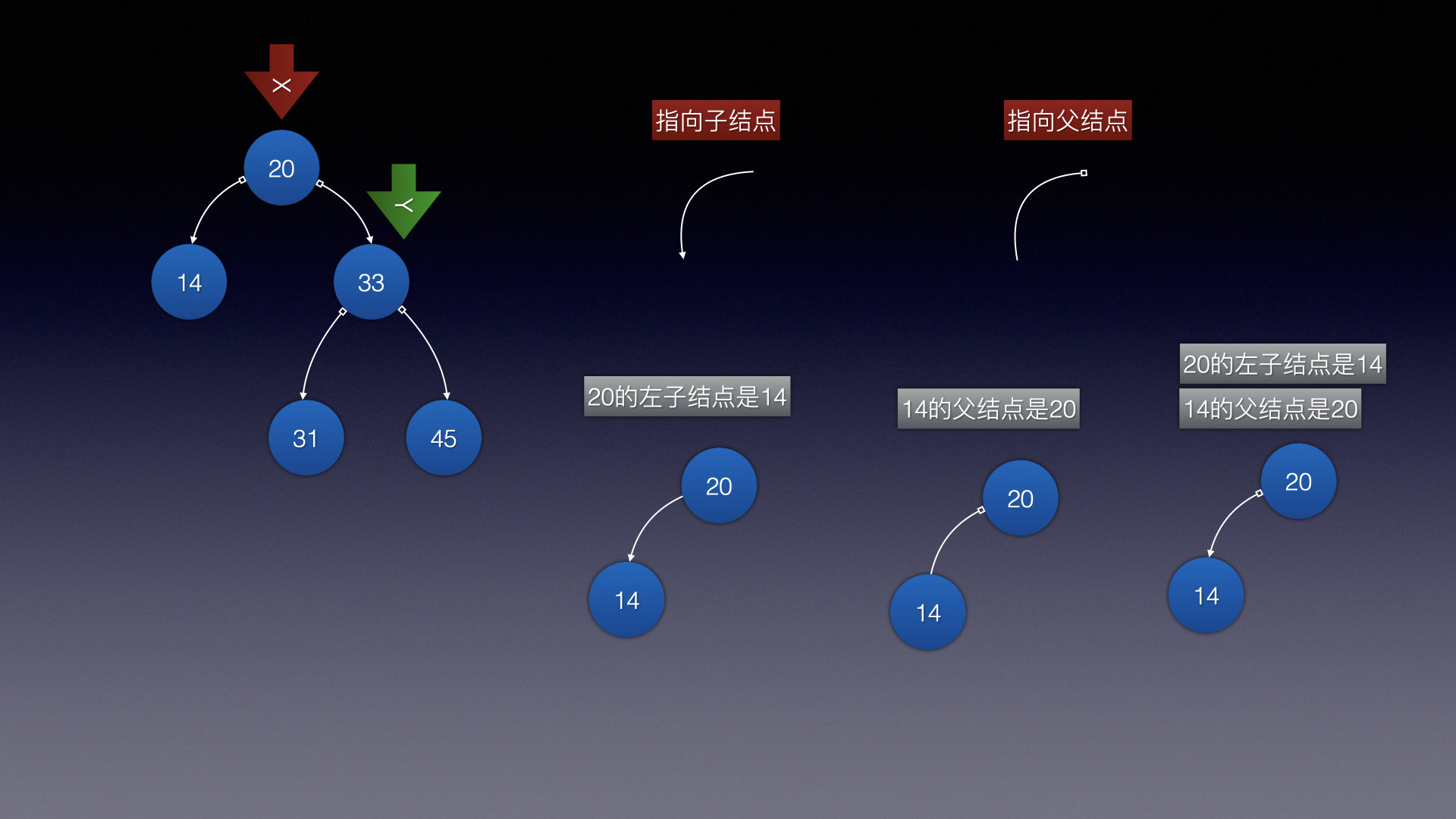
指向子结点(左子/右子结点)用实心三角表示

指向父结点用空心正方形表示

左旋

还是将具体步骤拆分开

将X的右子结点指向Y的右子结点
将Y的左子结点的父结点更新为X
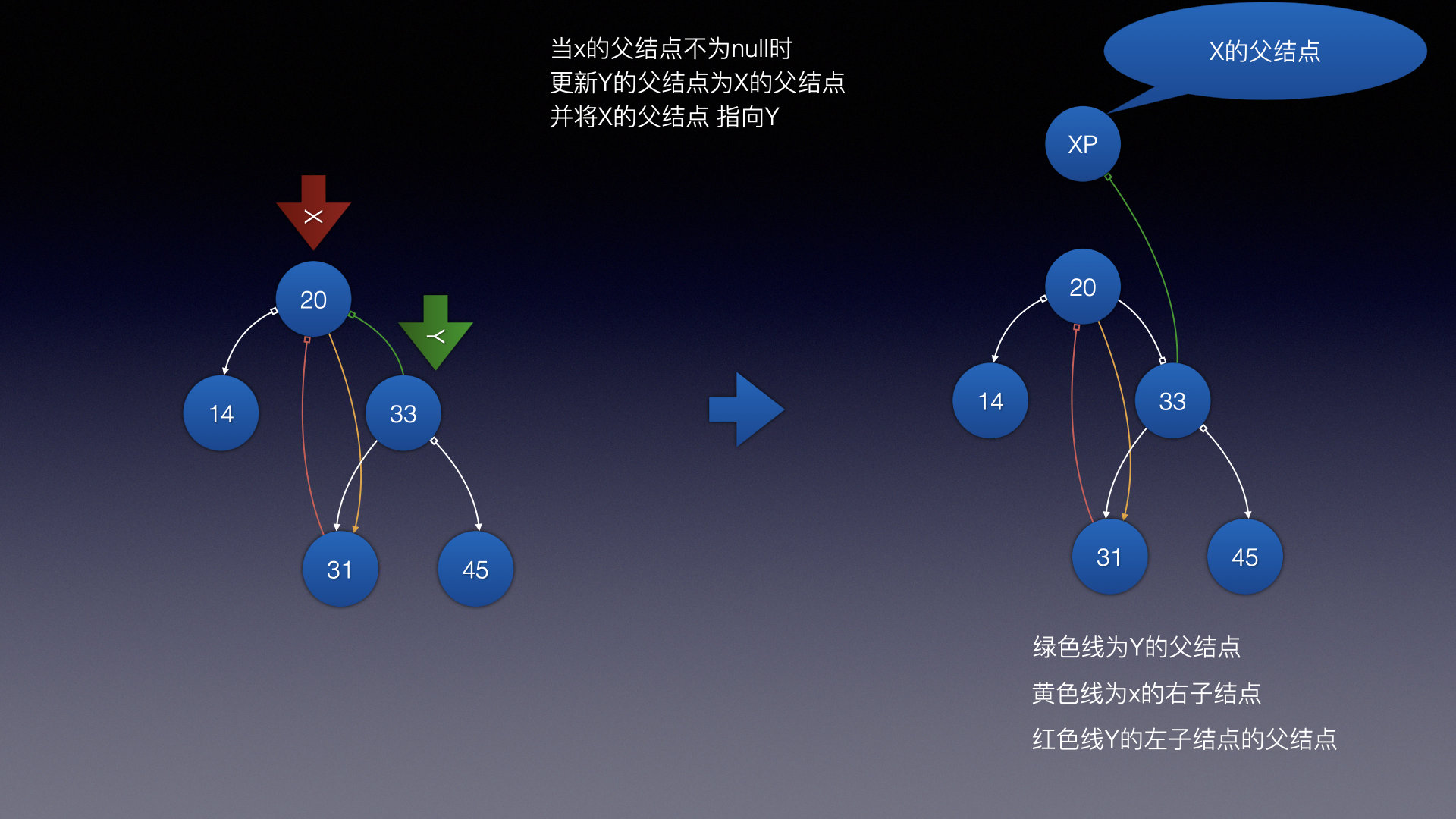
当x的父结点不为空时，更新y的父结点为x的父结点，并将x的父结点指定为y
将x的父结点更新为y 将y的左子结点更新为x

来看看具体步骤:

1.将X的右子结点指向Y的右子结点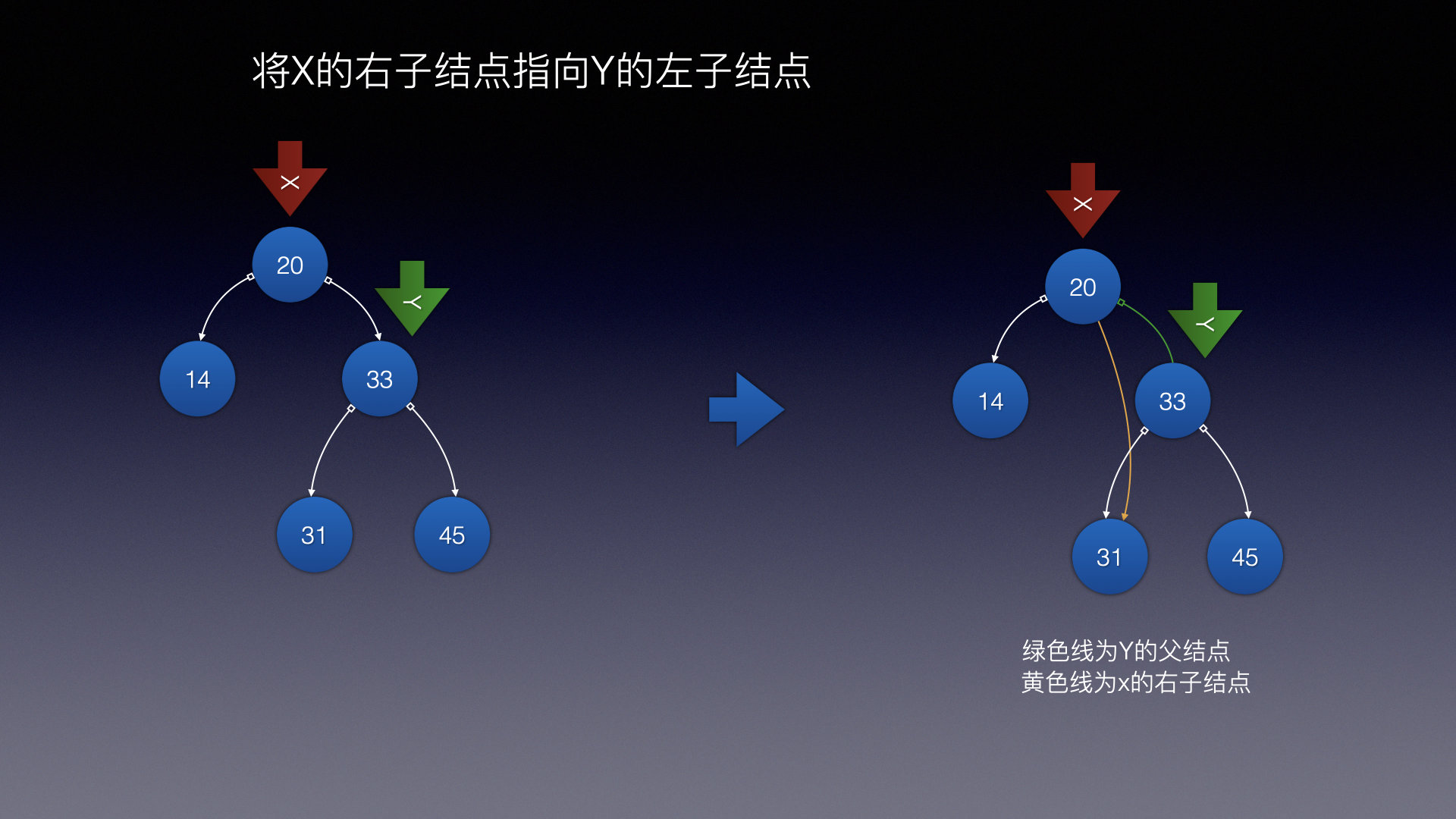

2.将Y的左子结点的父结点更新为X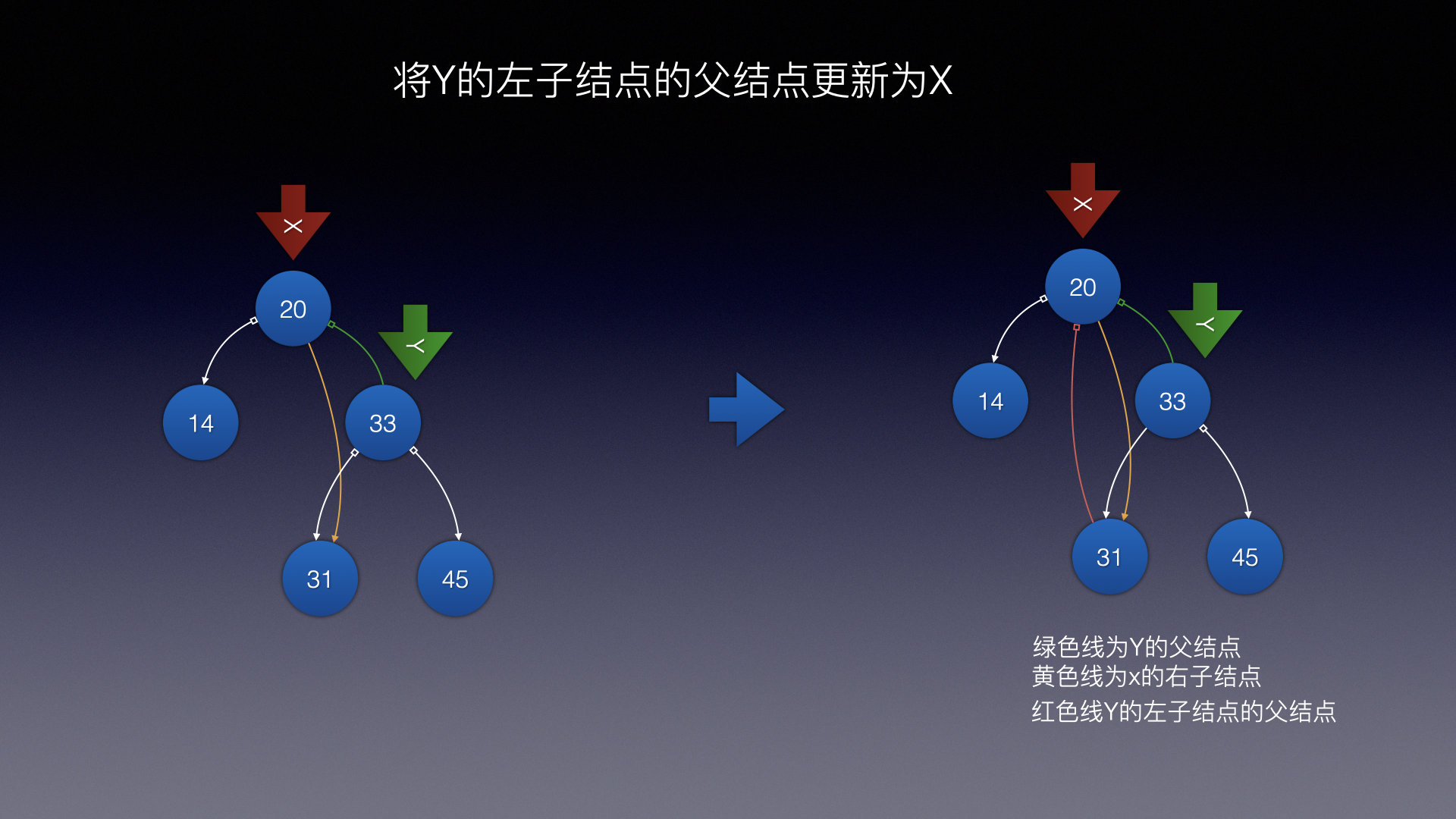

当x的父结点不为空时，更新y的父结点为x的父结点，并将x的父结点指定为y

将x的父结点更新为y 将y的左子结点更新为x

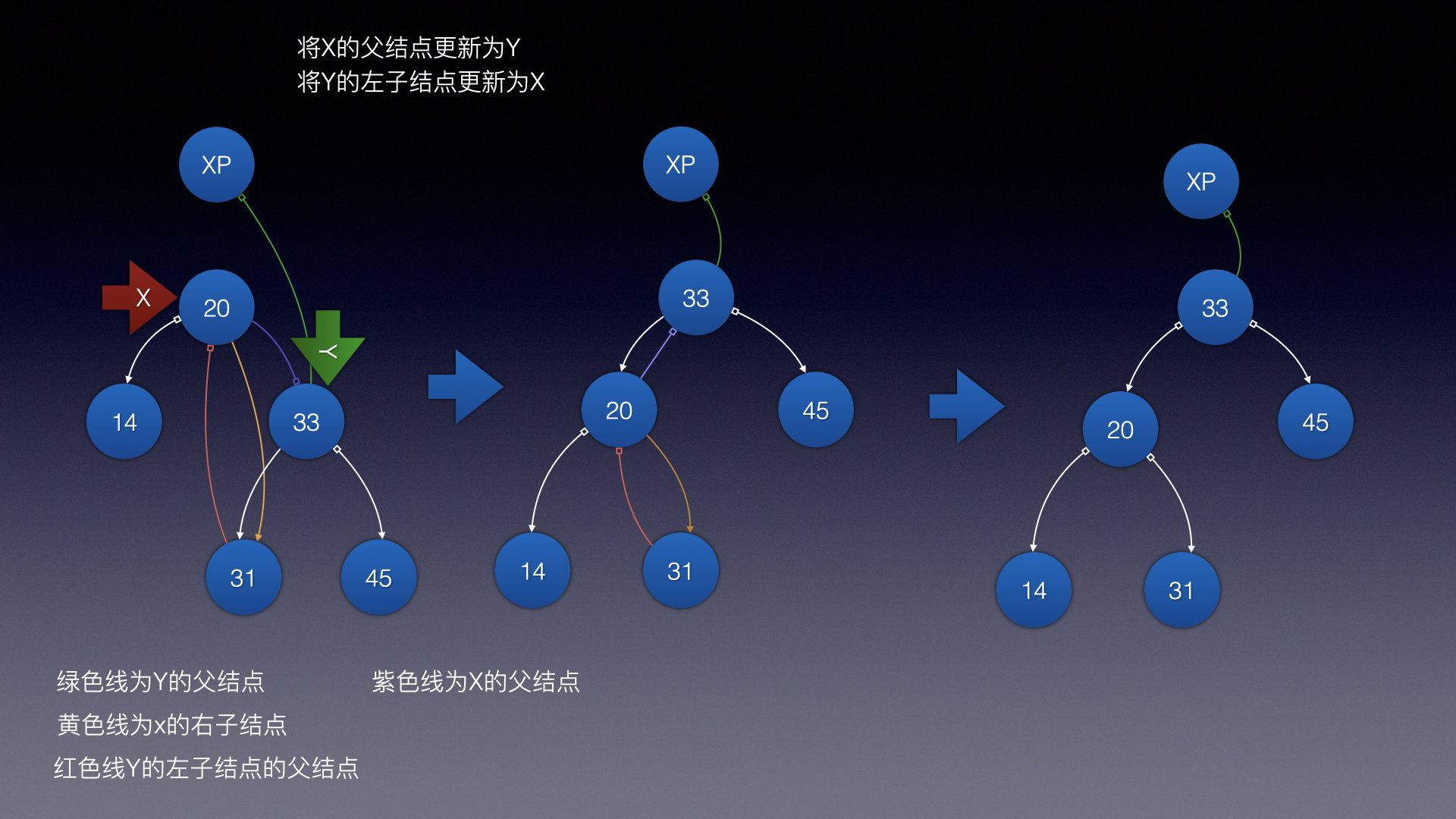
最终完成了左旋

右旋

将y的左子结点指向x的右子结点并且更新x的右子结点的父结点为y
当y的父结点不为空时，x.parentNode = y.parentNode
y的当前位置为 x
更新y的父结点为x, x的右子结点为y

道理和左旋相同,只是方向不同,这里就没画图了

插入结点情景分析

叔叔结点存在

情景1

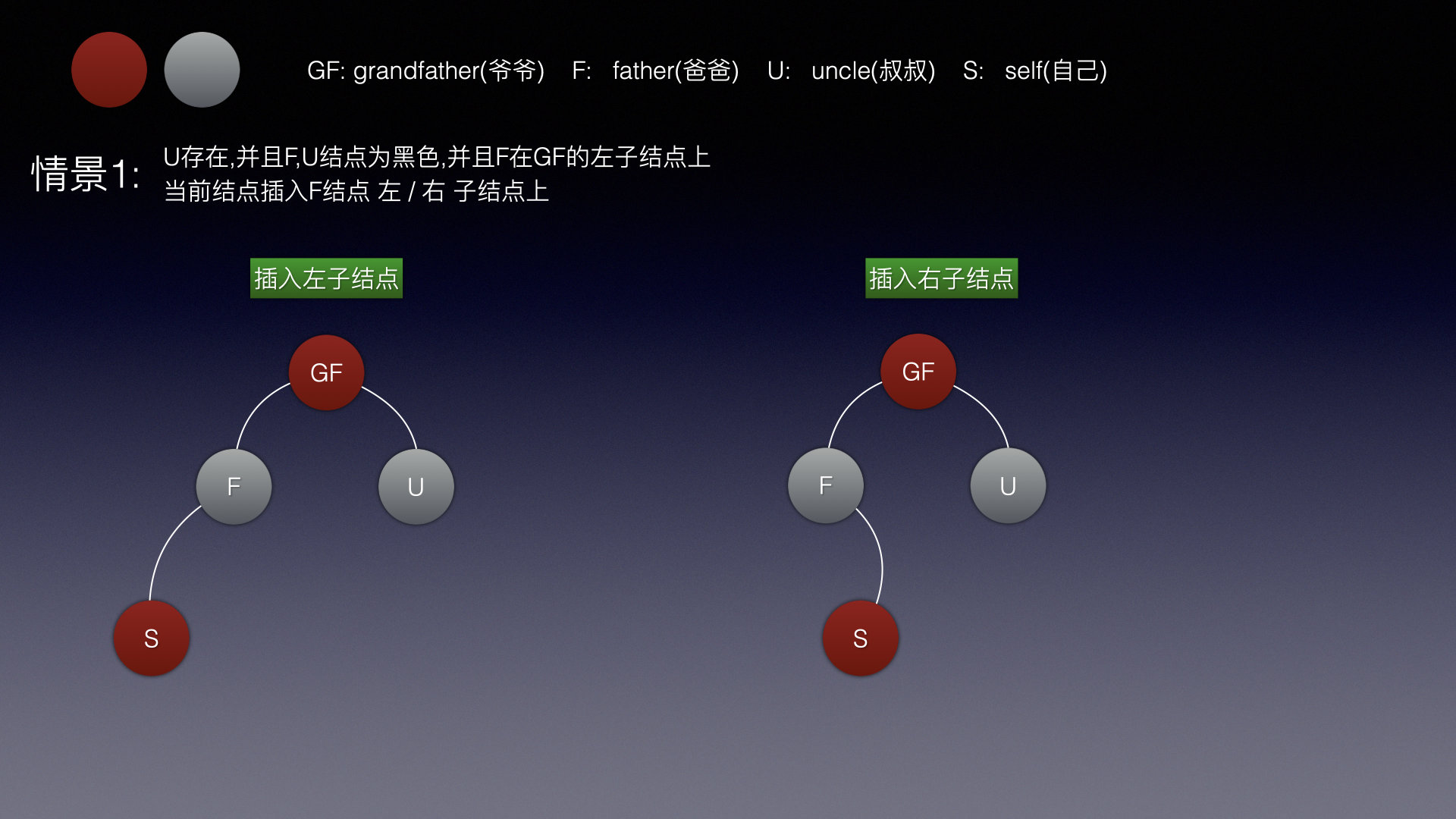
情景1又分为2种情况, 插入左子结点 / 右子结点,都是直接插入即可,

此时爷爷(GF)结点是红色,在以爷爷结点向上递归进行下一轮操作

情景2

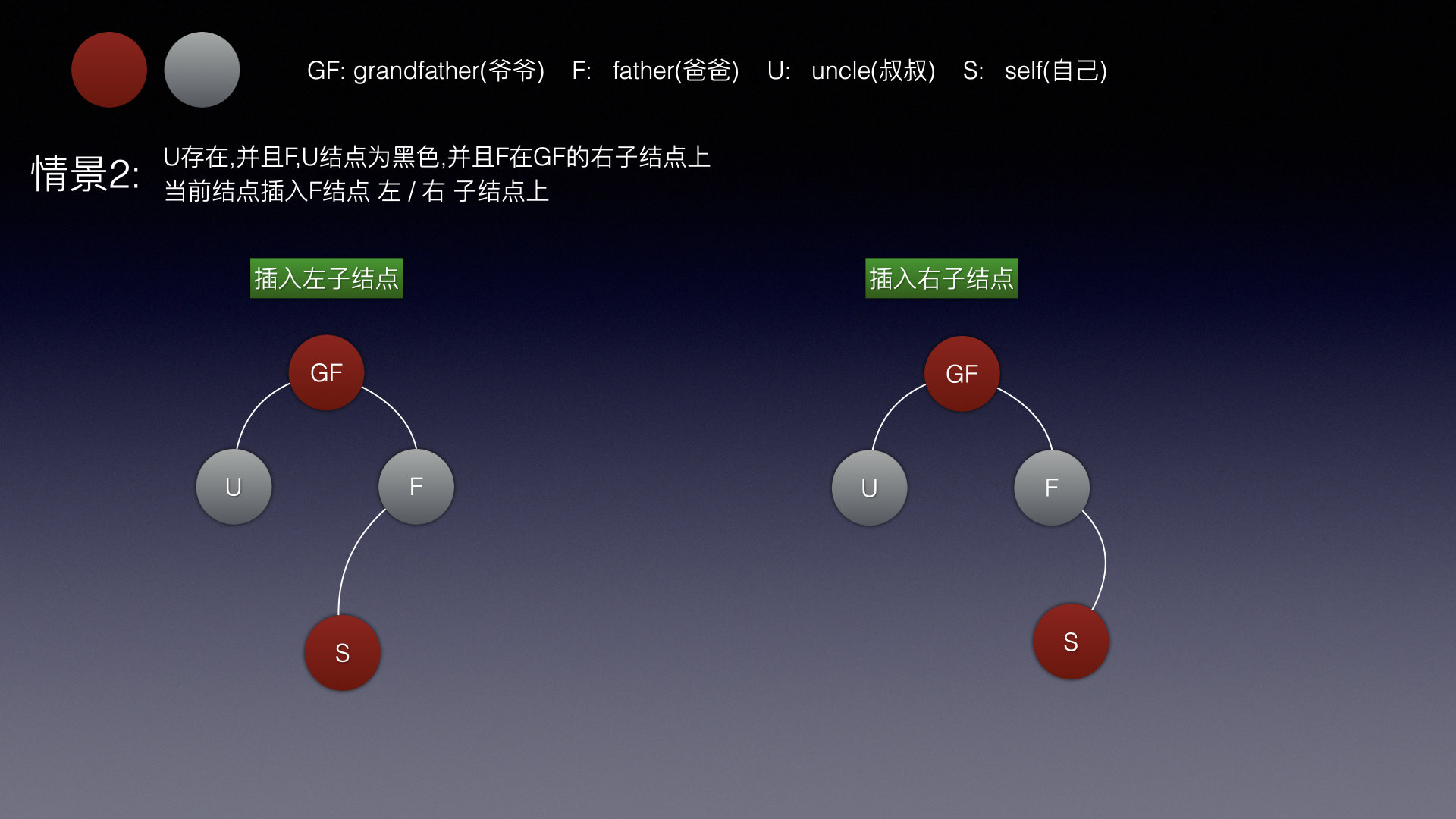
情景2和情景1是一样的,不同的就是插入反方向

情景3

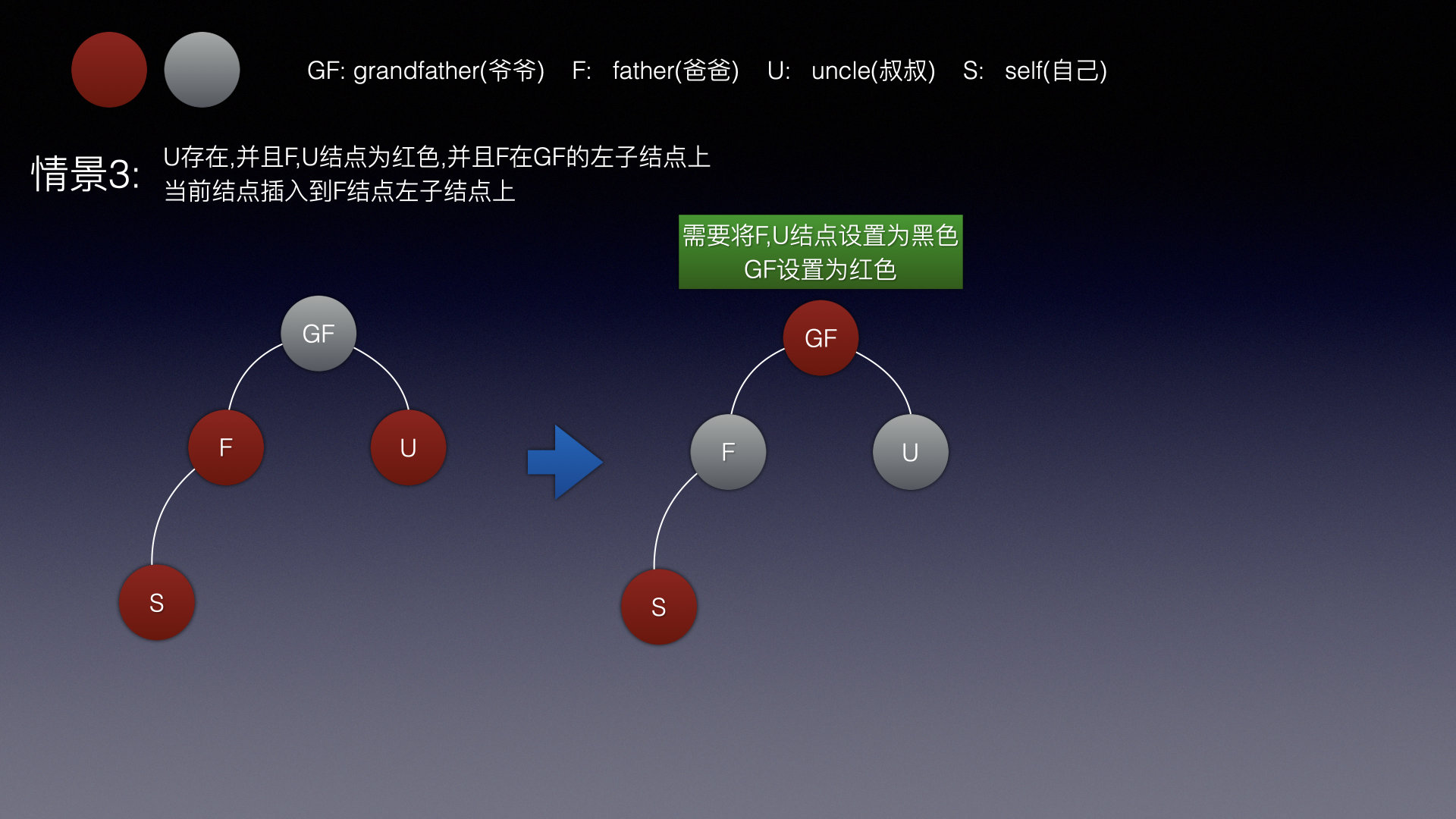
如果说爸爸结点和叔叔结点为红色,

那么需要将爸爸和叔叔改为黑色,并且爷爷改为红色

然后在以爷爷结点向上递归

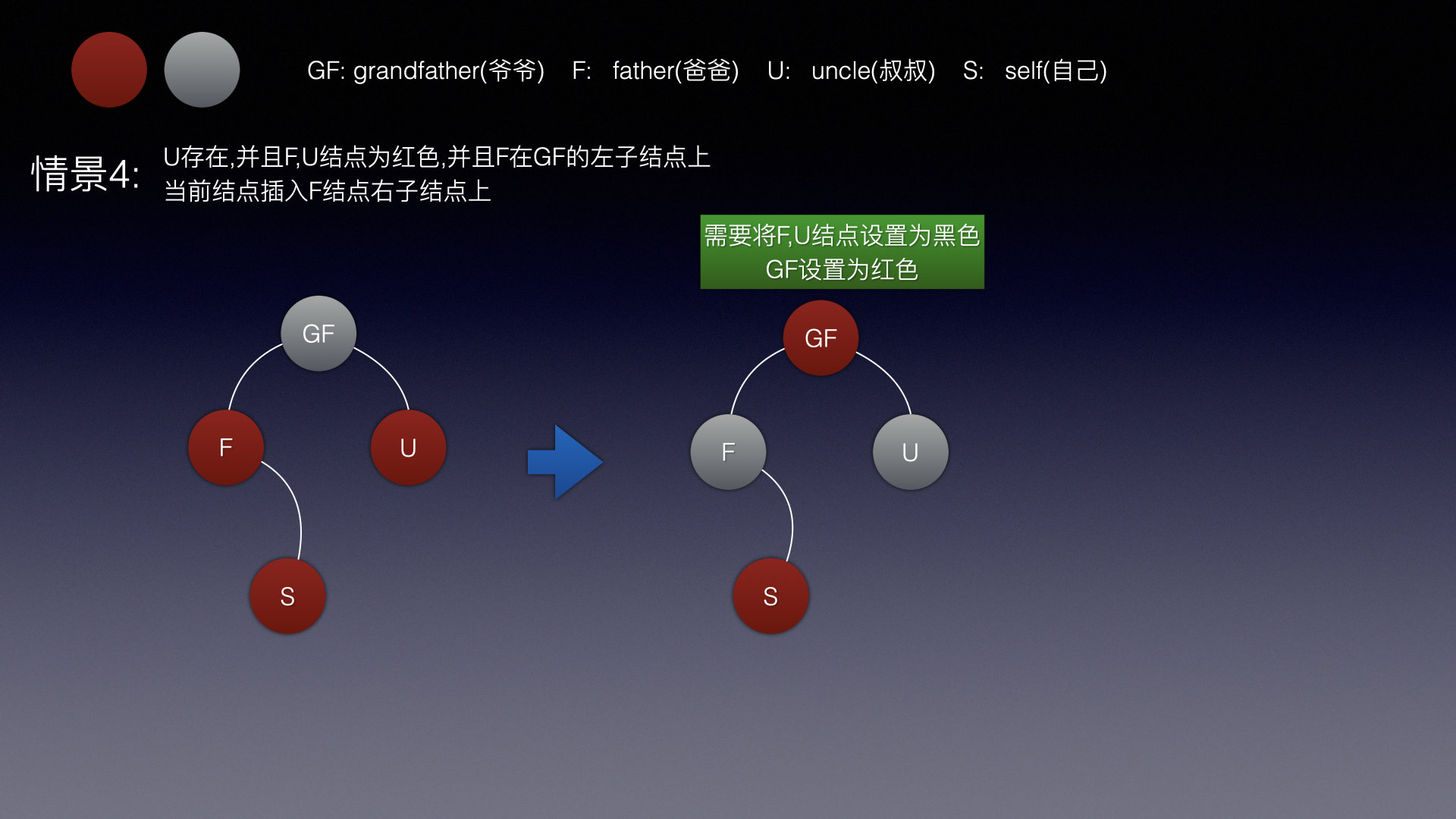
情景4

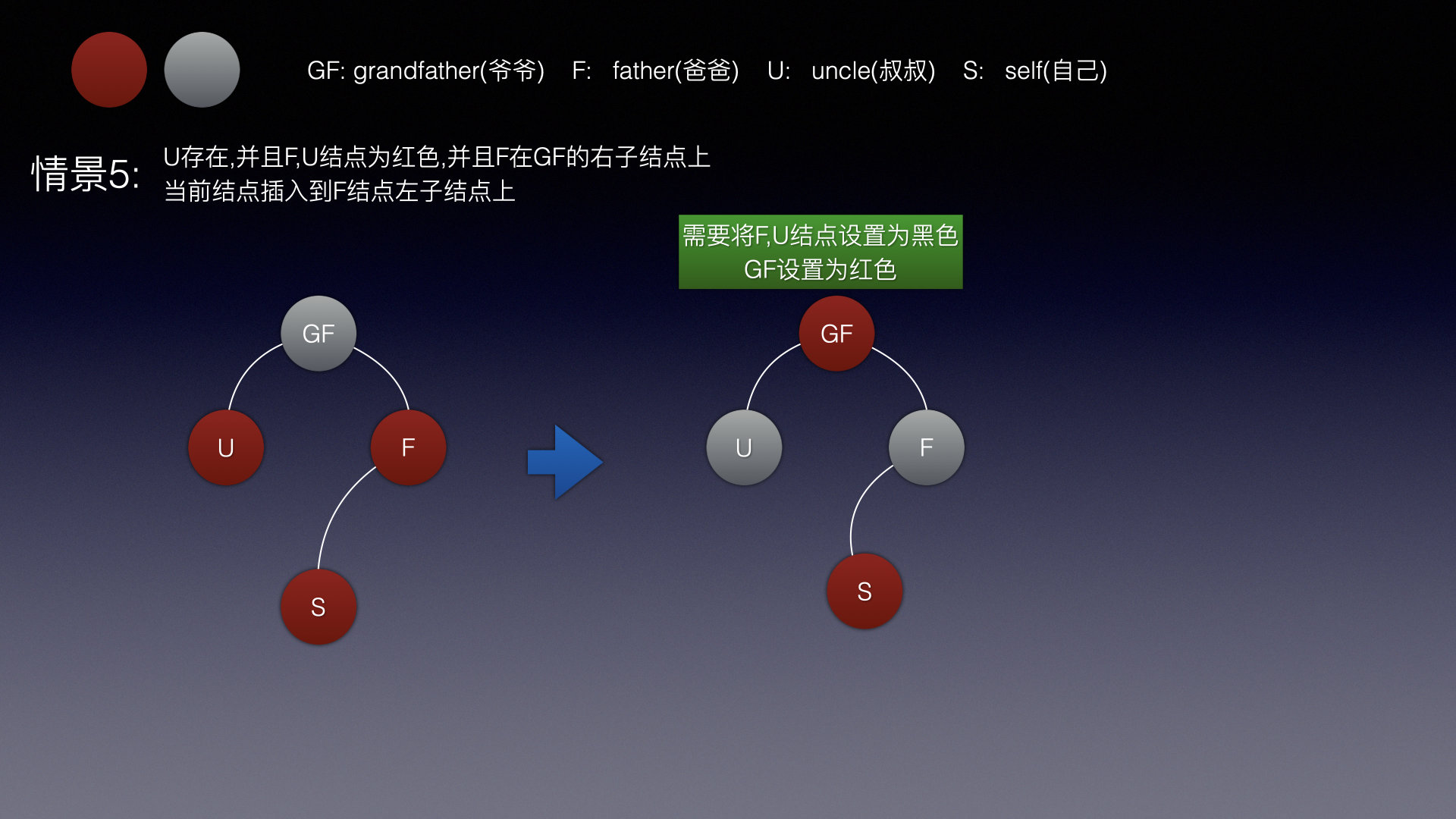
情景5

情景6

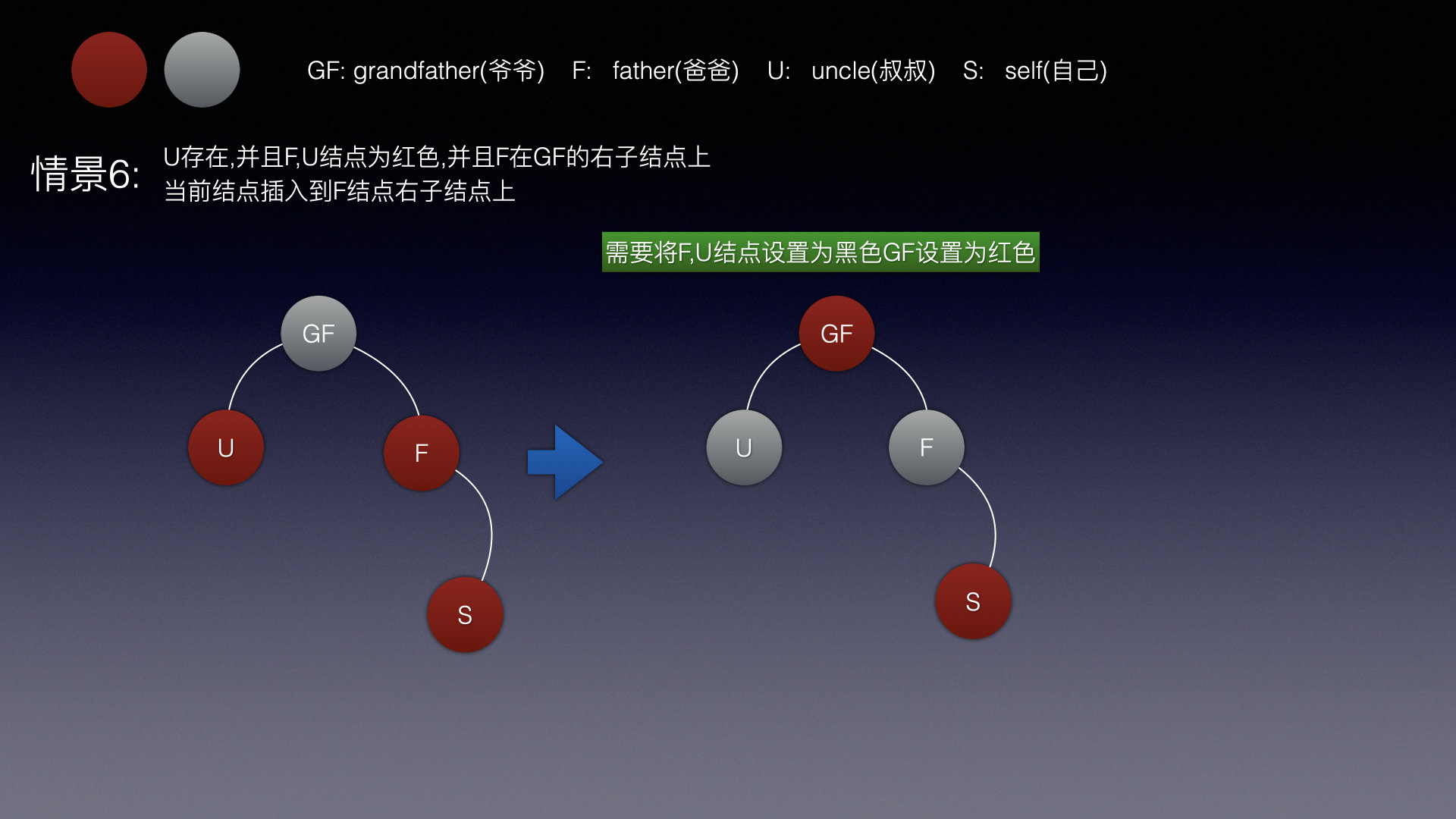
情景4,5,6都和情景3情况一样,爸爸和叔叔为红色,那么就将爸爸和叔叔改为黑色即可

情景6.1

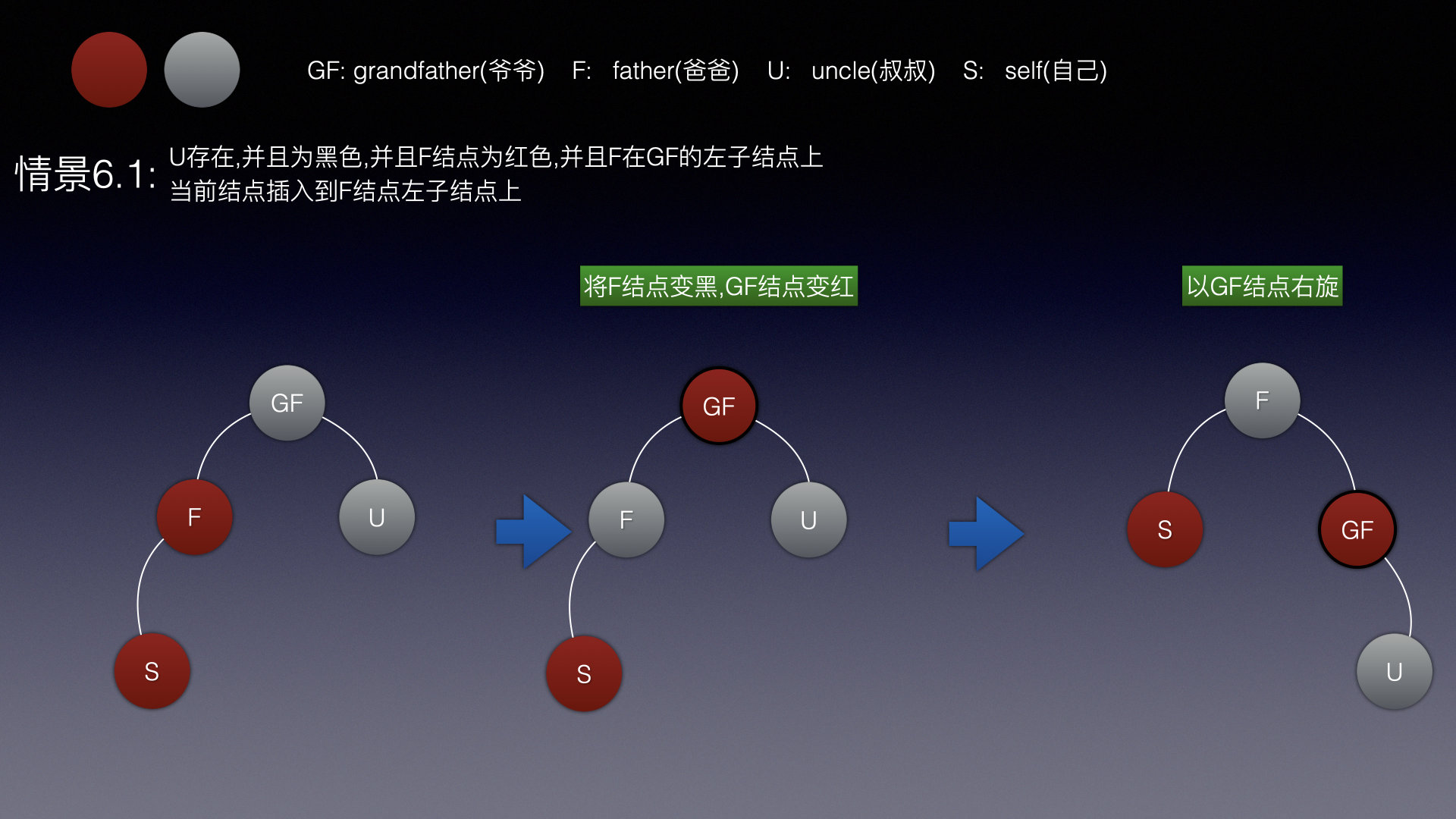
假如爸爸是红色 ,叔叔结点是黑色

因为当前插入结点一定是红色,导致自己和爸爸结点形成了双红,(LL双红)

所以说需要将爸爸染成黑色,爷爷染成红色

然后在以爷爷结点进行右旋即可

情景6.2

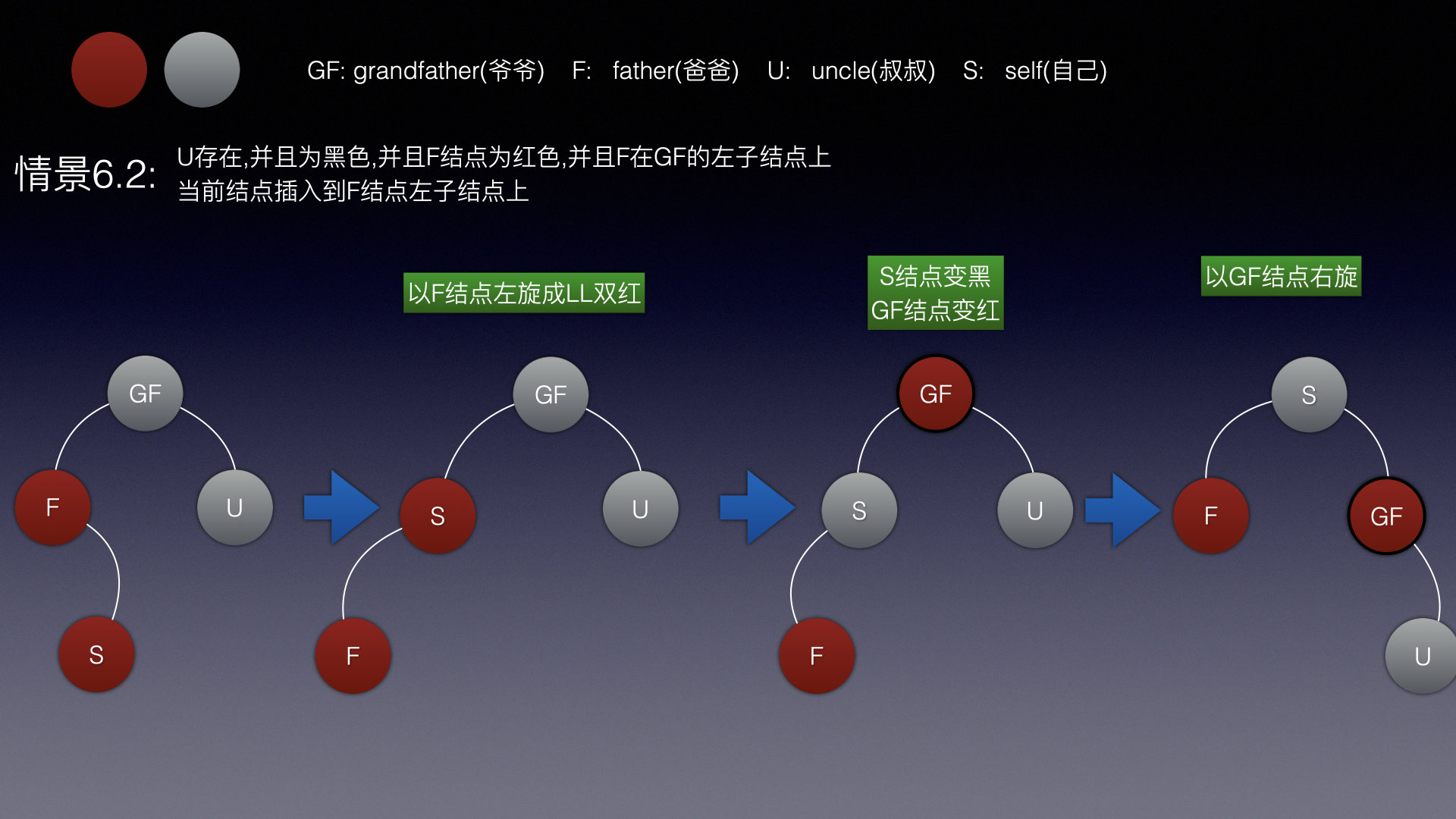
这也是同样的道理,先以父结点形成LL双红,然后在进行情景6.1的操作即可!

情景6.3

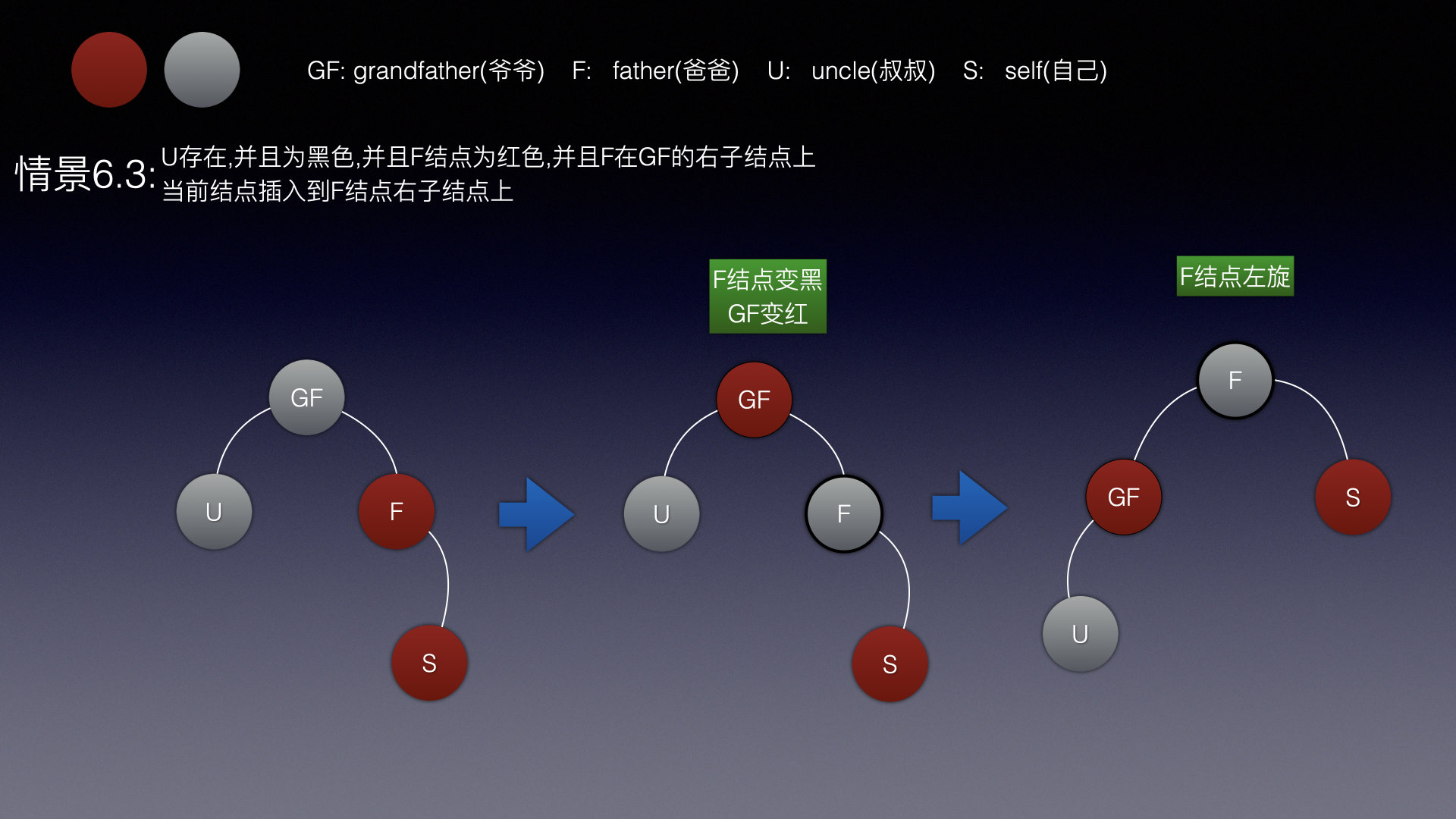
情景6.3就是插入爷爷结点的右子结点上,道理都是一样的

此时当前结点和父结点形成了RR双红,

需要将爸爸结点染成黑色,爷爷结点染成红色,然后以爷爷结点进行左旋

情景6.4

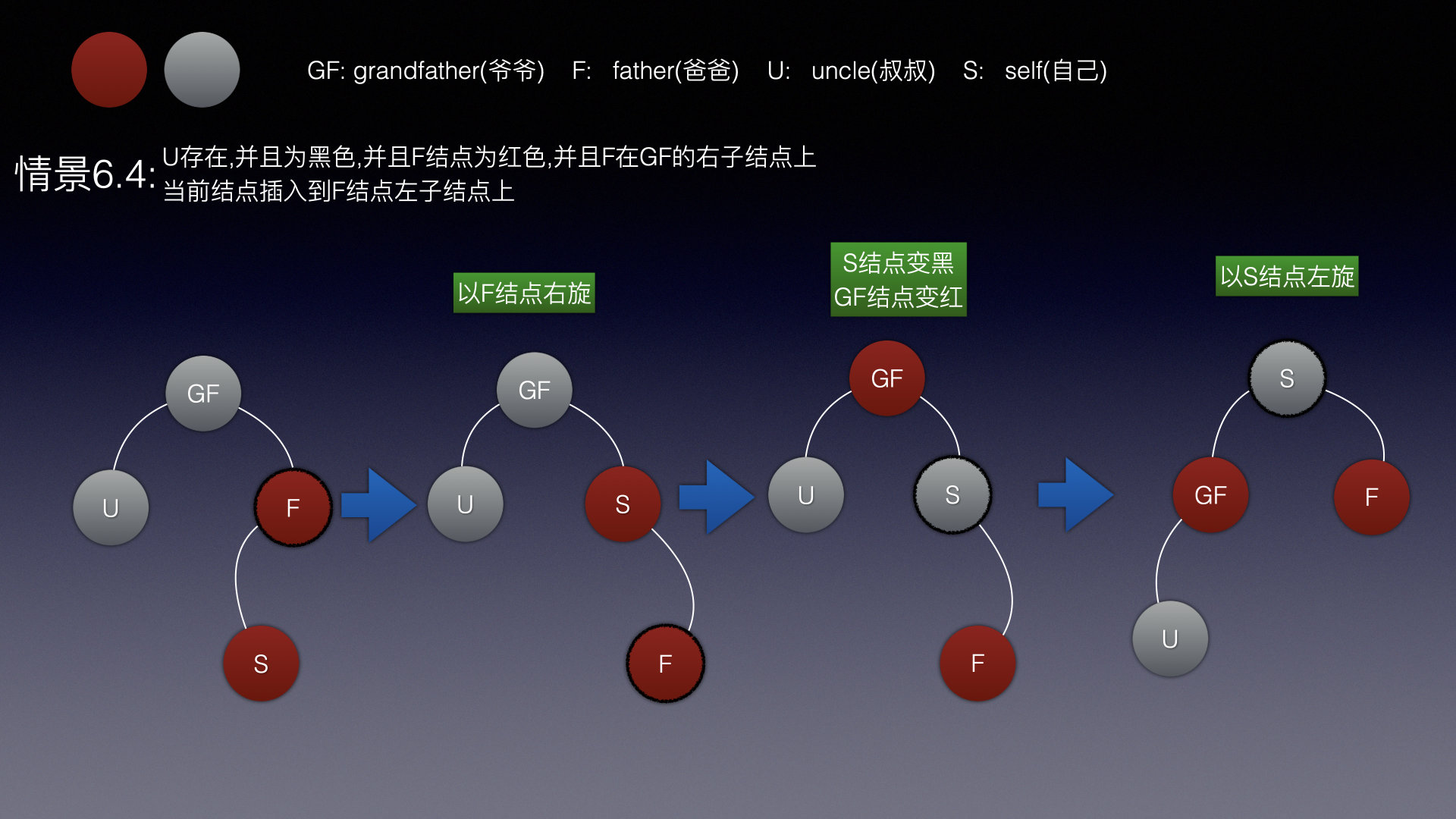
先旋转层RR双红,在进行情景6.3的操作

叔叔结点不存在

情景7

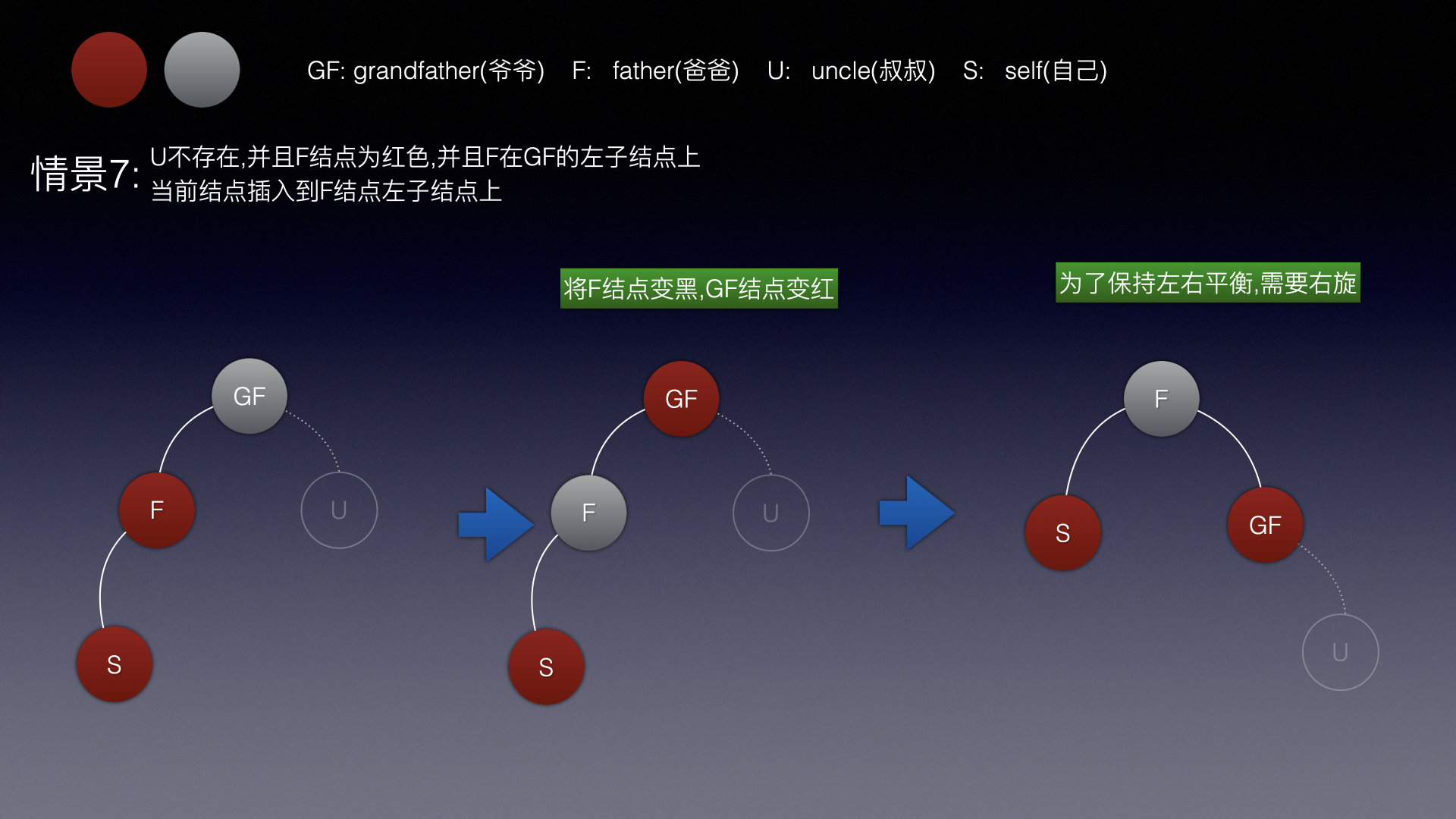
如果叔叔结点不存在,当前父结点为红色,

那么直接将父结点染成红色,爷爷结点染成黑色,并且右旋即可

情景8

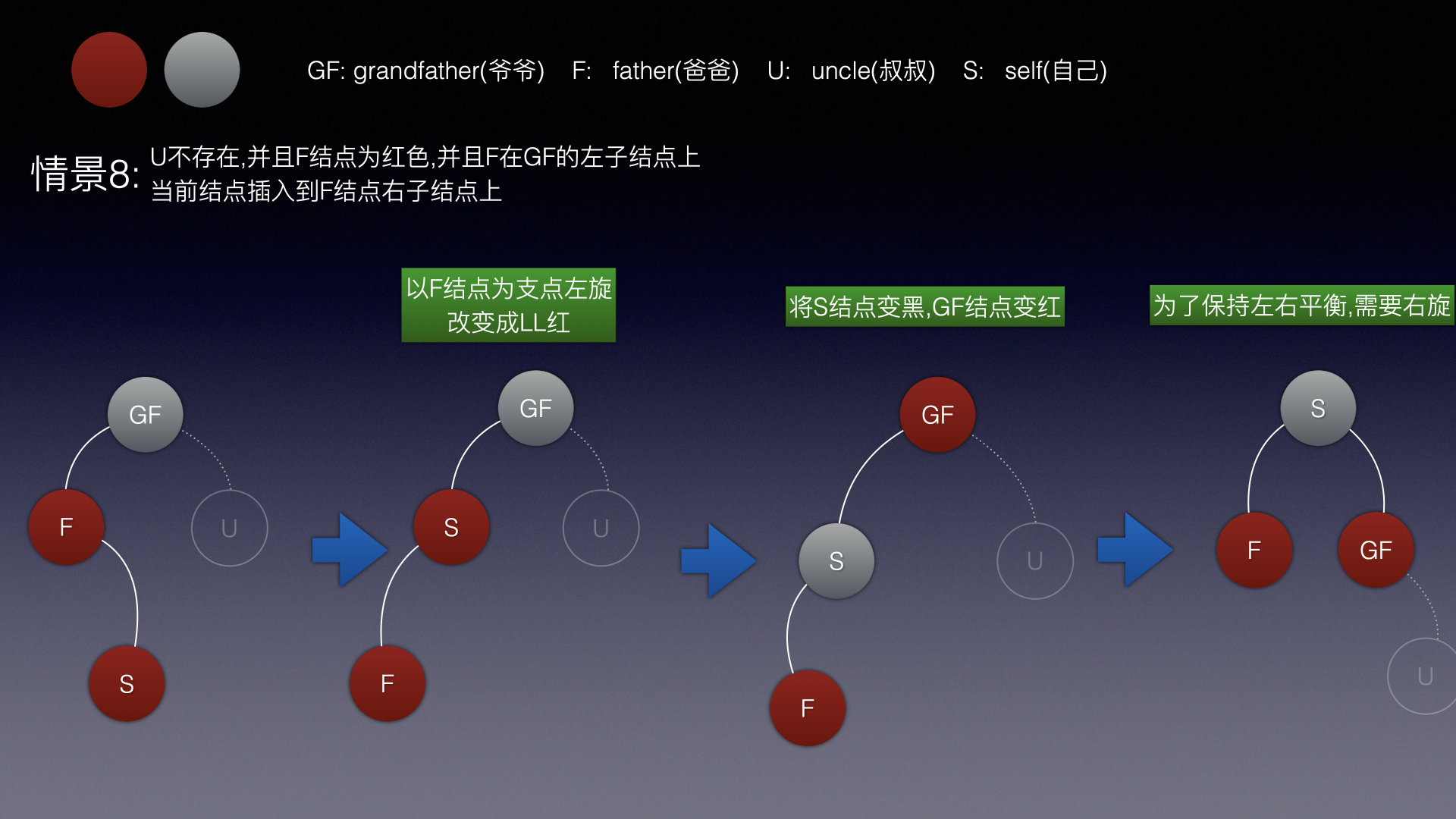
道理一样,先以爸爸结点左旋,旋转成LL双红

然后进行情景7的操作即可

情景9

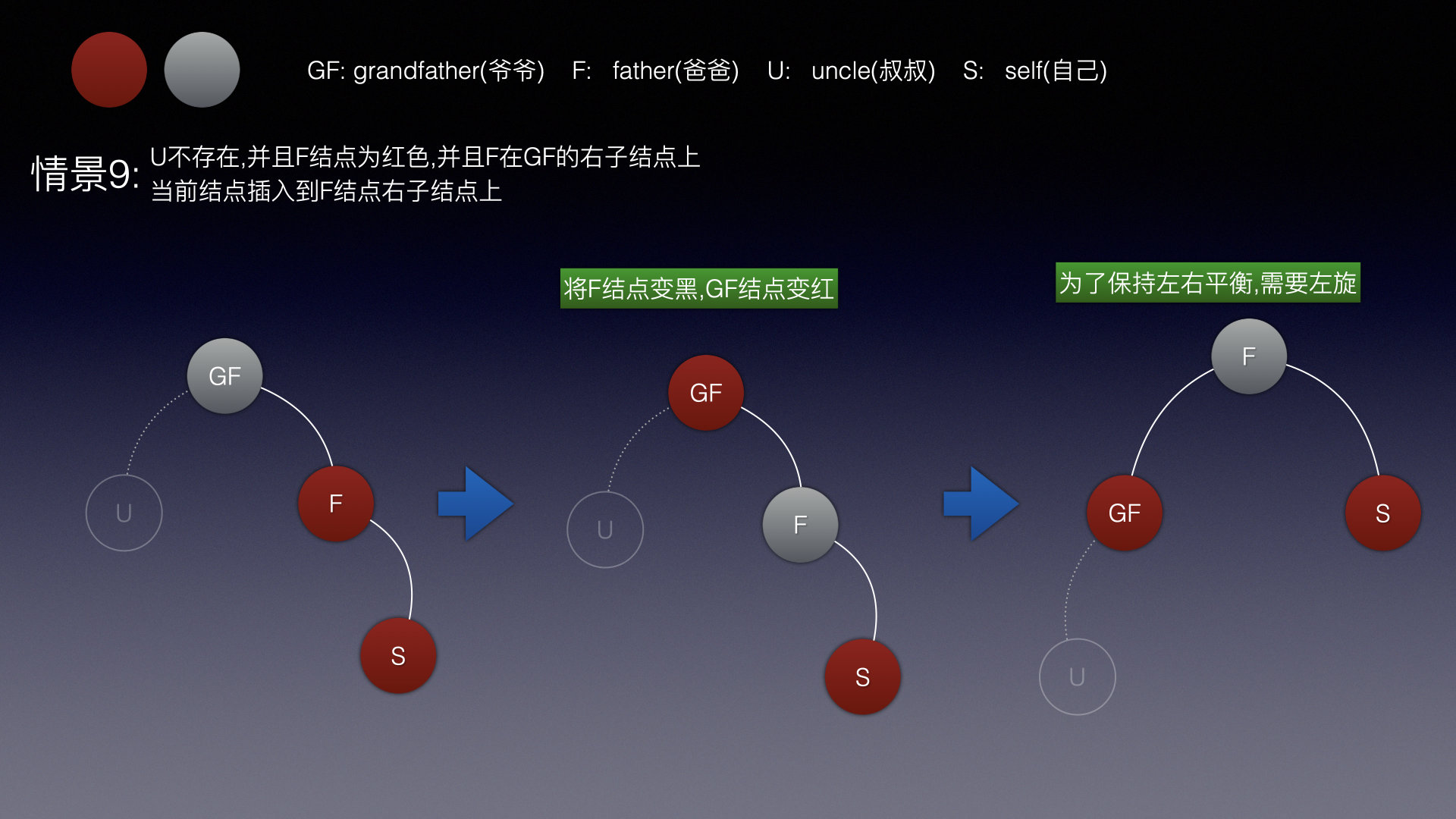
同样的道理,现在是RR双红,直接将爸爸结点染成红色,爷爷结点染成黑色,然后左旋即可

情景10

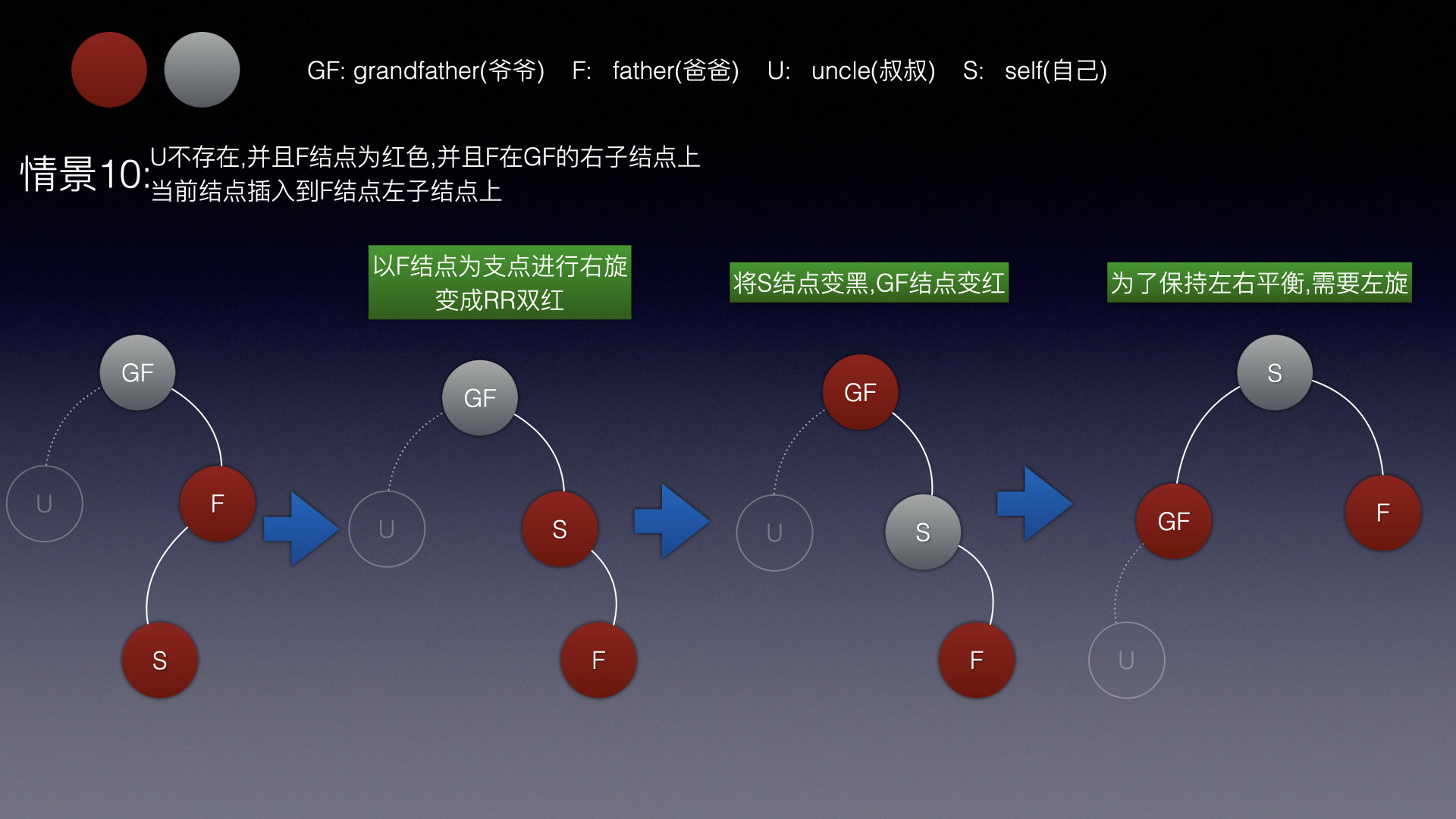
和情景9类似

此时情景分析就差不多了,先来看看一棵红黑树构建的完整流程!

完整流程图

最终结果:

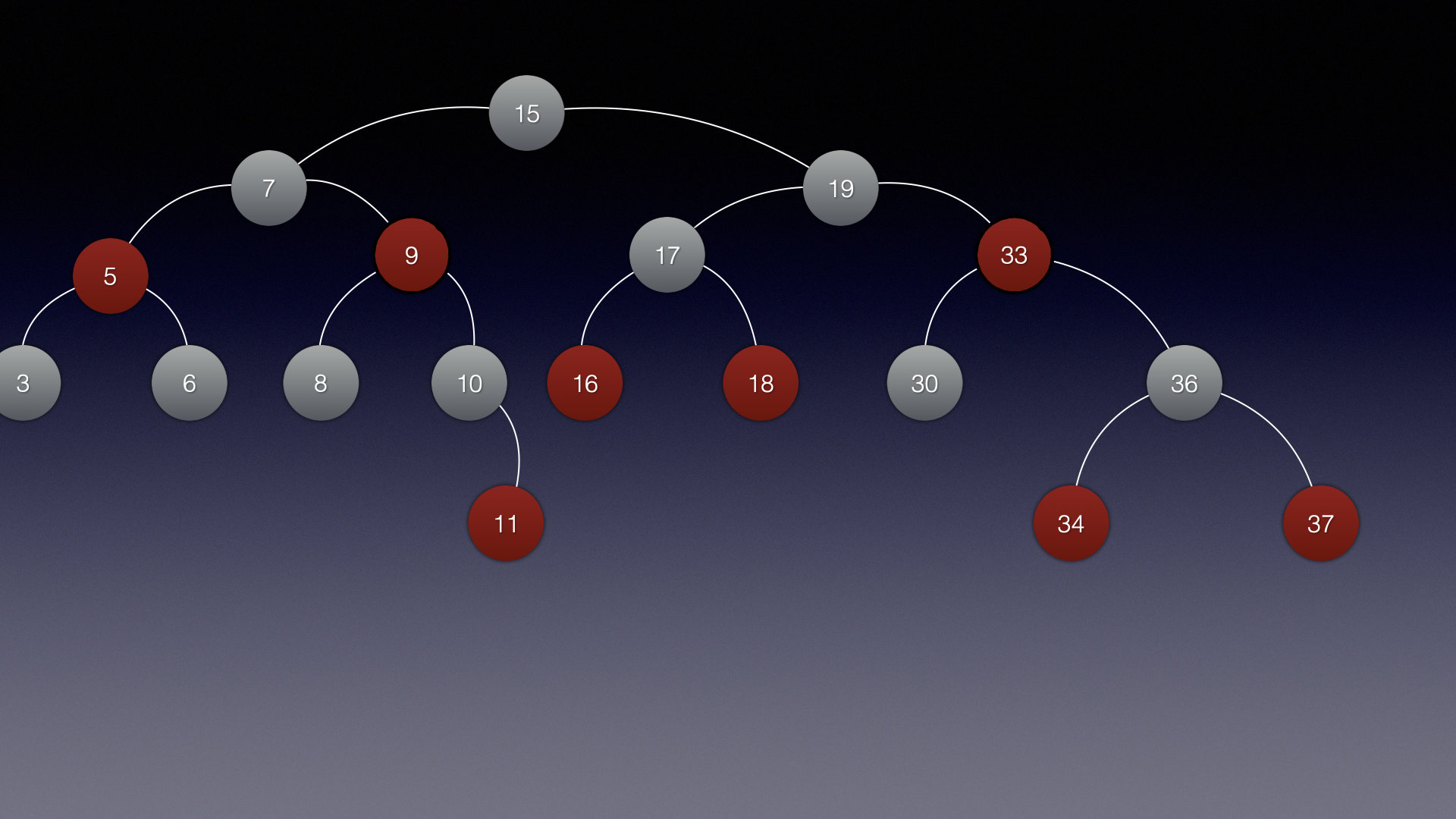
获取重要结点

这里重要结点就值的是爸爸结点,叔叔结点,爷爷结点等

获取父结点

# RBTree.java
  
public void add(int value) 

    RBNode tempRoot = root;
    RBNode parentNode = null;
    // 添加结点
    RBNode node = new RBNode(null, null, RED, value);

    while (tempRoot != null) 
        // 记录上一个结点
        parentNode = tempRoot;
        // 如果左子结点不为null 并且 当前值比左子结点的值要小，说明还在左侧
        if (node.value <= tempRoot.value) 
            tempRoot = tempRoot.leftNode;
         else 
            // node.value > tempRoot.value
            tempRoot = tempRoot.rightNode;
        
    

    // TODO 设置父结点
    node.parentNode = parentNode;

    if (parentNode != null) 
        // 如果当前结点比父结点大 说明当前结点在父结点右侧
        if (node.value > parentNode.value) 
            parentNode.rightNode = node;
         else 
            // 反之在左侧
            parentNode.leftNode = node;
        

    

    // 开始修复 (保证满足红黑树要求)
    restore(node);

获取爷爷结点

父结点是node.parentNode.

那么爷爷结点就是

grandFatherNode = node.parentNode.parentNode

获取叔叔结点

# RBTree.java
// 父结点
RBNode parentNode = node.parentNode;

// 叔叔结点
RBNode uncleNode = null;

if (node.parentNode != null && node.parentNode.parentNode != null) 
    // 爷爷结点
    grandFatherNode = node.parentNode.parentNode;

    // 如果当前结点为GF结点的左侧
    if (grandFatherNode.leftNode == parentNode) 
        // 那么叔叔结点就是GF结点的右侧
        uncleNode = grandFatherNode.rightNode;
     else 
        // 反之
        uncleNode = grandFatherNode.leftNode;

完整代码

知道这些前置条件,并且知道具体情景该如何对应操作下,那么代码就是一些 if else 了

直接来看完整代码

 /*
     * @author: android 超级兵
     * @create: 2022/6/23 11:16
     * TODO 进行修复 保证树是一颗红黑树
     */
    private void restore(RBNode node) 
        // 默认根节点是黑色
        root.color = BLACK;

        // 当前结点
        RBNode selfNode = node;

        // 父结点
        RBNode parentNode = node.parentNode;

        // GF = grandFather
        // TODO 爷爷结点
        // tips: 如果父结点为红色 那么一定存在爷爷结点，因为根节点一定是黑色
        RBNode grandFatherNode = null;

        // TODO 叔叔结点
        RBNode uncleNode = null;
        if (node.parentNode != null && node.parentNode.parentNode != null) 
            grandFatherNode = node.parentNode.parentNode;

            // 如果当前结点为GF结点的左侧
            if (grandFatherNode.leftNode == parentNode) 
                // 那么叔叔结点就是GF结点的右侧
                uncleNode = grandFatherNode.rightNode;
             else 
                // 反之
                uncleNode = grandFatherNode.leftNode;
            
        

        // 叔叔结点存在
        if (uncleNode != null) 

            // 如果父亲结点和 叔叔结点 都为黑色 那么直接添加 TODO【参考情景1.png 和 情景2.png】
            if (isBlack(parentNode) && isBlack(uncleNode)) 
                // 啥操作不用干 上面已经添加了!
            
            // 如果父亲结点 和叔叔结点都为红色 TODO【参考 情景3.png,情景4.png,情景5.png,情景6.png】
            if (isRed(parentNode) && isRed(uncleNode)) 
                // 设置父亲结点和叔叔结点为黑色
                setColor(parentNode, BLACK);
                setColor(uncleNode, BLACK);
                setColor(grandFatherNode, RED);

                // 以红色结点处理
                restore(grandFatherNode);
            

            if (isRed(parentNode) && isBlack(uncleNode)) 
                // 如果父亲结点为红色 并且叔叔结点为黑色

                if (grandFatherNode.leftNode == parentNode) 
                    // 父结点在左侧
                    if (parentNode.leftNode == node) 
                        // TODO 查看 情景6.1.png
                        // 当前结点在左侧 TODO [LL双红]
                        setColor(parentNode, BLACK);
                        setColor(grandFatherNode, RED);
                        rightRotate(grandFatherNode);

                     else 
                        // TODO 查看 情景6.2.png
                        // 当前结点在右侧
                        leftRotate(parentNode);
//                        setColor(parentNode, BLACK);
                        setColor(grandFatherNode, RED);
                        rightRotate(grandFatherNode);

                        // 以红色结点向上递归
                        restore(grandFatherNode);
                    

                 else 
                    // 父结点在右侧
                    if (parentNode.leftNode == node) 
                        // TODO 查看 情景6.4.png
                        // 当前结点在左侧
                        // 父结点右旋 TODO【RR双红】
                        rightRotate(parentNode);
//                        setColor(parentNode, BLACK);
                        setColor(grandFatherNode, RED);

                        leftRotate(grandFatherNode);
                        // 以红色结点向上递归
                        restore(grandFatherNode);
                     else 
                        // TODO 查看 情景6.3.png
                        // 当前结点在右侧
                        setColor(parentNode, BLACK);
                        setColor(grandFatherNode, RED);
                        leftRotate(grandFatherNode);
                    
                
            

        
        else 
            // 叔叔结点不存在

            // 父亲结点为红色
            if (isRed(parentNode)) 

                // 判断当前父结点是在祖父的左侧还是右侧
                if (grandFatherNode != null && grandFatherNode.leftNode == parentNode) 
                    // 父亲在祖父左侧

                    // 判断当前结点在父亲的左侧还是右侧 TODO【参考 情景7.png】
                    if (parentNode.leftNode == node) 
                        // 在父亲左侧

                        // 设置父亲结点黑色 祖父结点红色
                        setColor(parentNode, BLACK);
                        setColor(grandFatherNode, RED);

                        rightRotate(grandFatherNode);

                        // 以红色结点进行递归
                        restore(grandFatherNode);

                     else 
                        // 在父亲右侧 TODO【参考 情景8.png】
                        // 先以父结点为支点左旋
                        leftRotate(parentNode);
                        // 设置父亲结点黑色 祖父结点红色
                        setColor(parentNode, BLACK);
                        setColor(grandFatherNode, RED);
                        // 以红色结点进行递归
                        restore(grandFatherNode);
                    
                 else 
                    // 父亲在祖父右侧

                    // 判断父结点是否在祖父结点右侧
                    // 父结点在祖父结点右侧

                    // 当前结点是否在父结点右侧 TODO [参考 情景9.png]
                    if (parentNode.rightNode == node) 
                        // 当前结点在父结点右侧
                        // 染色
                        setColor(parentNode, BLACK);
                        setColor(grandFatherNode, RED);
                        // 以祖父结点左旋
//                        grandFatherNode.leftRotate();
                        leftRotate(grandFatherNode);
                        // 以红色结点进行递归
                        restore(grandFatherNode);
                     else 
                        // 父结点在祖父结点左侧 TODO 【参考 情景10.png】

                        // 当前结点在父结点左侧
                        // 先右旋
//                        parentNode.rightRotate();
                        rightRotate(parentNode);
                        setColor(parentNode, BLACK);
                        setColor(grandFatherNode, RED);

                        // 以红色结点进行递归
                        restore(grandFatherNode);

tips:代码一定要结合着示意图来看,我这里都标注清晰了,下载代码看看吧~~

看到这里,树结构基本能拿的出手了… 同时也祝自己生日快乐 🎂 嘻嘻 @__@

完整代码

原创不易,您的点赞就是对我最大的支持!

上一篇:2-3树,2-3-4树,B树 B+树 B*树了解

以上是关于数据结构与算法:树红黑树的主要内容，如果未能解决你的问题，请参考以下文章

红黑树与JAVA实现

红黑树原理

C++进阶数据结构_红黑树

数据结构与算法:树 红黑树

前言

2-3树 映射红黑树

2-3-4树 映射红黑树

角色分析

定义结点

旋转

左旋

右旋

插入结点情景分析

叔叔结点存在

情景1

情景2

情景3

情景4

情景5

情景6

情景6.1

情景6.2

情景6.3

情景6.4

叔叔结点不存在

情景7

情景8

情景9

情景10

完整流程图

获取重要结点

获取父结点

获取爷爷结点

获取叔叔结点

完整代码

数据结构与算法:树红黑树

2-3树映射红黑树

2-3-4树映射红黑树