计算机视觉中的深度学习6: 反向传播
Posted SuPhoebe
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了计算机视觉中的深度学习6: 反向传播相关的知识,希望对你有一定的参考价值。
Slides:百度云 提取码: gs3n
神经网络的梯度下降
我们之前在学习线性分类器的时候,使用Loss函数以及梯度下降法来更新权重。那么对于神经网络,我们该如何计算每层神经元的权重呢?
对每层W直接求导(愚蠢的方法)
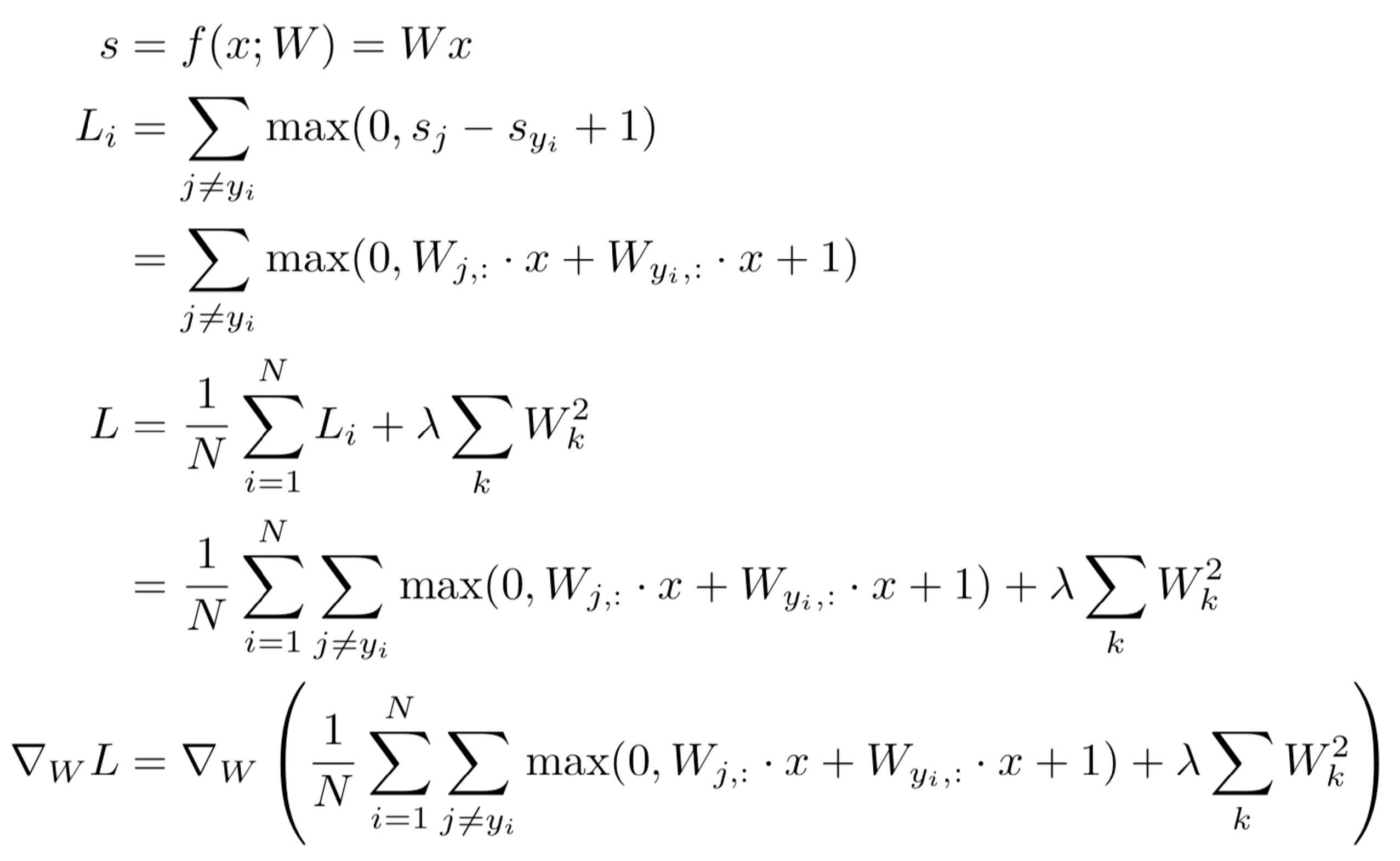
如上公式所示,Loss函数最终是能被表达成由各层W组成的函数公式,并且也完全有可能直接对其进行求导。
问题
- 非常乏味,需要大量矩阵演算,需要大量纸张
- 如果我们想改变损失怎么办? 例如。 使用softmax代替SVM? 需要从头开始重新派生。这种方式不是模块化的。
- 对于非常复杂的NN模型不可行!
计算图
公式
f
(
x
,
y
,
z
)
=
(
x
+
y
)
z
f(x,y,z)=(x+y)z
f(x,y,z)=(x+y)z的计算图如下

例子1
- 向前传播过程
- q = x + y , f = q z q = x+y\\ \\ , \\ f=qz q=x+y , f=qz
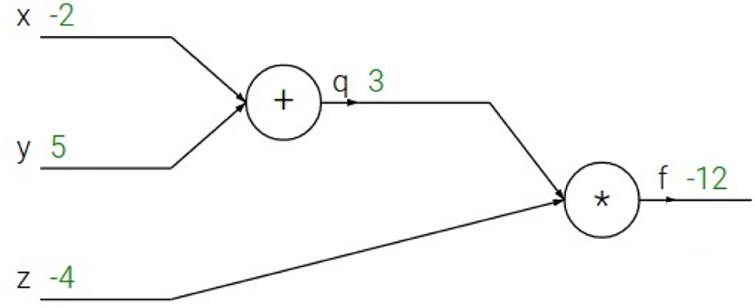
- 反向传播过程
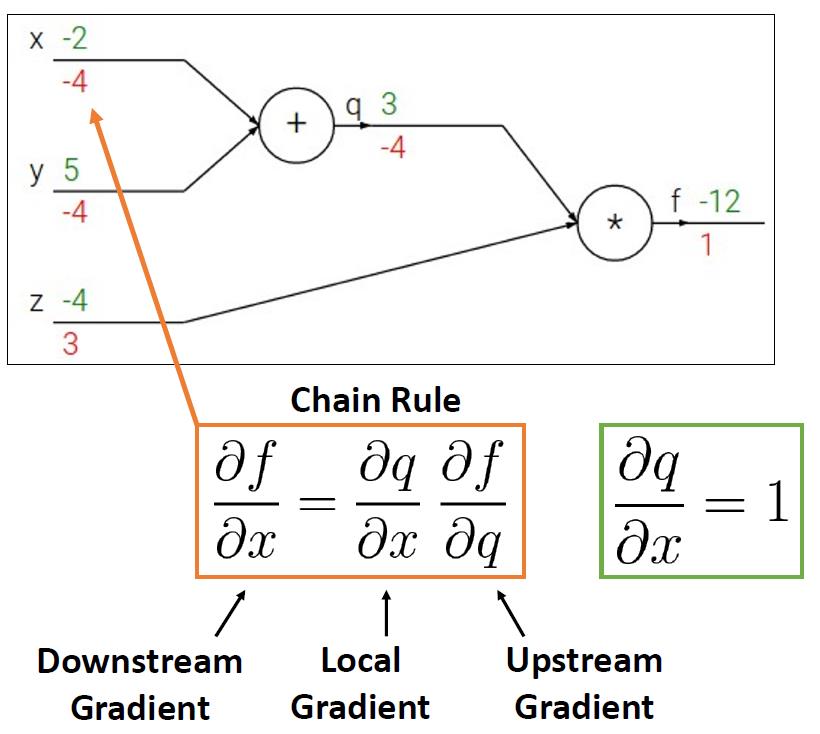
- 我们想要的是 ∂ f ∂ x \\partial f\\over \\partial x ∂x∂f, ∂ f ∂ y \\partial f\\over \\partial y ∂y∂f, ∂ f ∂ z \\partial f\\over \\partial z ∂z∂f
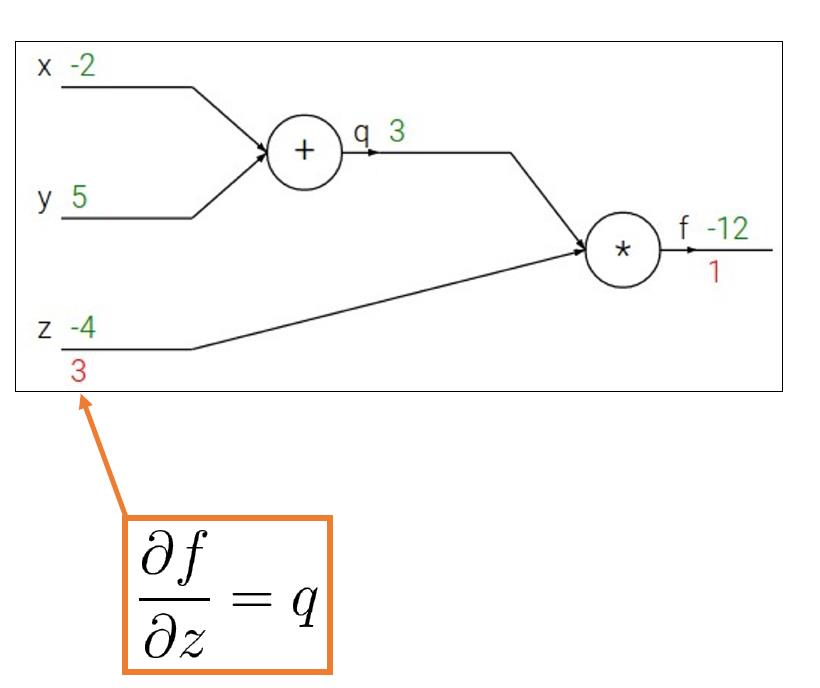
- 用链式规则可以得到如下的公式
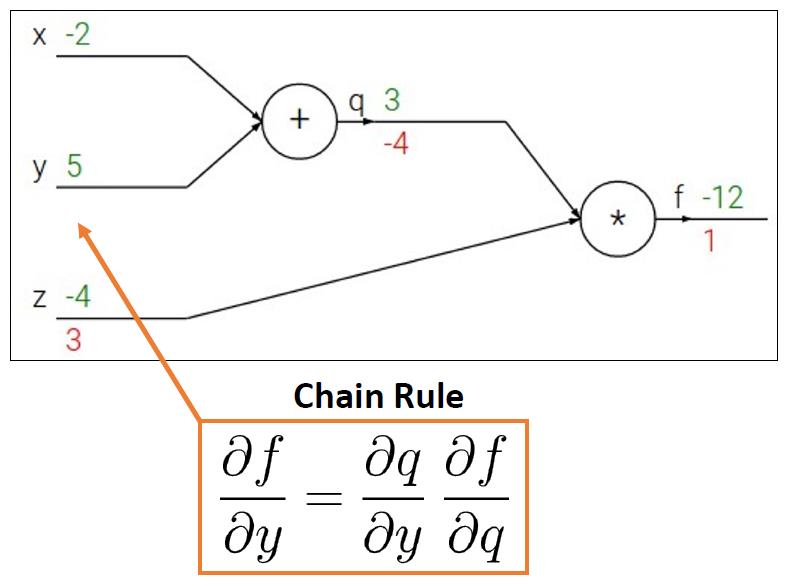
- 同理对于
∂
f
∂
x
\\partial f\\over \\partial x
∂x∂f,我们是很容易能够得出对于当前节点位置的偏导是什么的
例子2
公式为
f
(
x
,
w
)
=
1
1
+
e
−
(
w
0
x
0
+
w
1
x
1
+
w
2
)
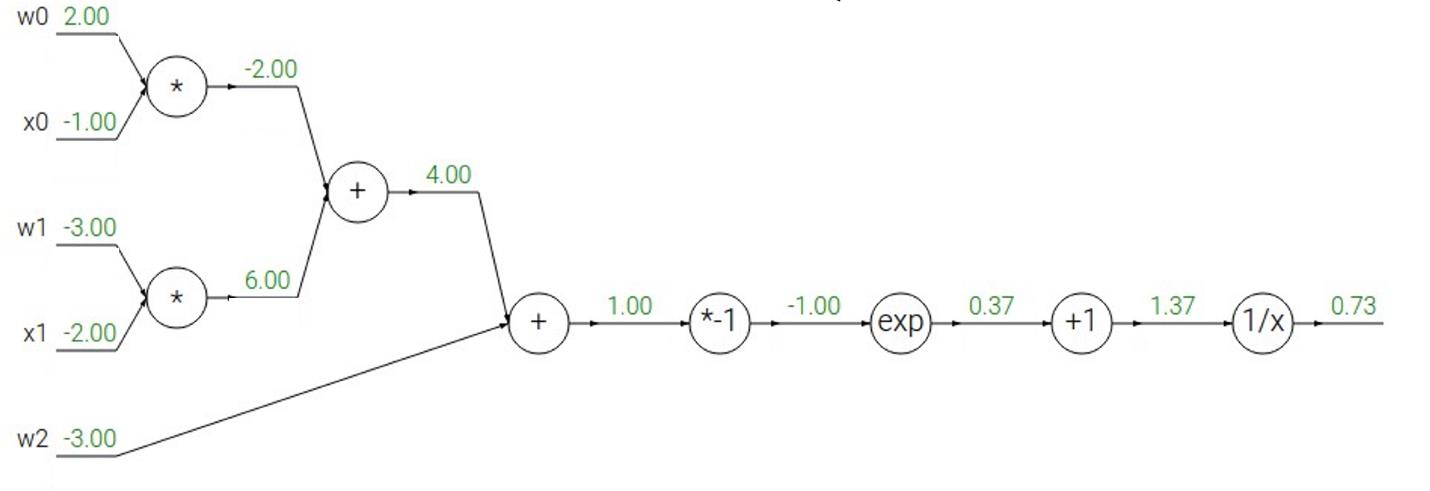
f(x,w)=1\\over 1+e^-(w_0x_0+w_1x_1+w_2)
f(x,w)=1+e−(w0x0+w1x1+w2)1
向前传播过程
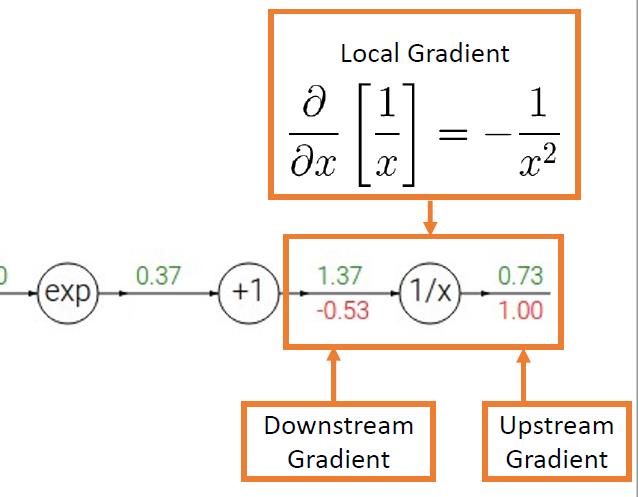
反向传播的第一部分
−
0.53
=
−
1
1.3
7
2
-0.53 = -1\\over 1.37^2
−0.53=−1.3721
反向传播的第三步
−
0.2
=
e
−
1.0
∗
−
0.53
-0.2 = e^-1.0 * -0.53
−0.2=e−1.0∗−0.53
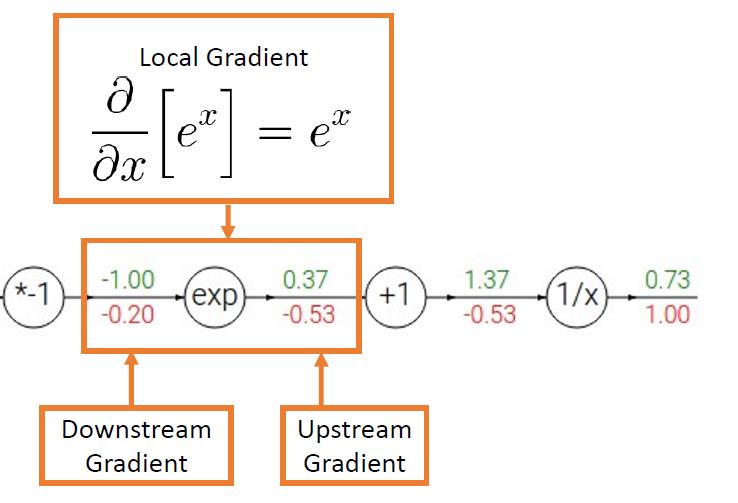
这个例子就非常具体地显示了怎么计算本地梯度以及连式法则的运用。
模块API设计
对于每一个神经层,在实现这个神经层的时候,都会知道输入输出的矩阵长宽,以及激活函数的使用。所以在pytorch,tensorflow等实现的时候,都已经实现好了这个激活函数和输入输出矩阵的节点向前传播,向后传播的函数,直接将这个节点拿去使用即可。

向量化
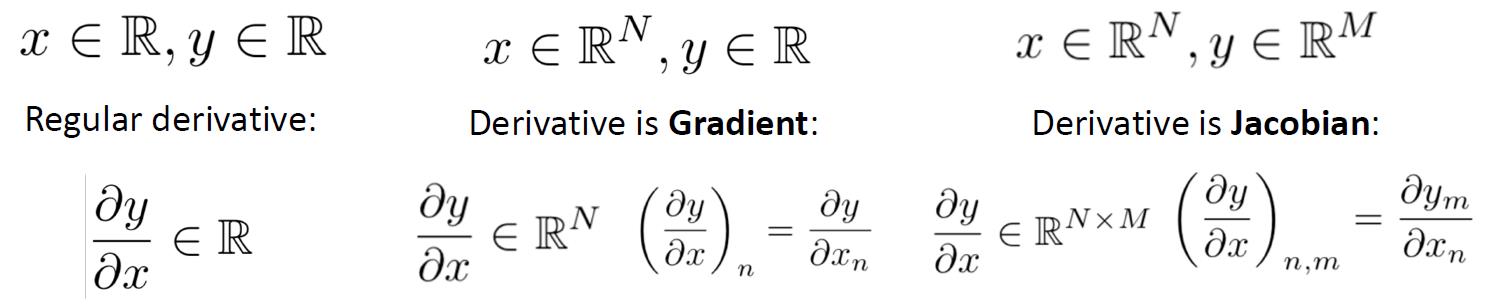
第一例为单输入单输出,第二列为输入向量,输出单数,第三列为输入输出向量
例子1
对于一个4输入4输出的函数,我们可以得出它的Jacobian矩阵如下

我们可以发现,Jacobian矩阵大部分都是0;这是一个非常常见的情况,Jacobian矩阵是非常非常稀疏的,所以绝对不要显式地表示Jacobian矩阵,而是应该用隐式的方式去压缩。
例子2
矩阵输入,矩阵输出,感兴趣的可以看看幻灯片里面的具体讲解

以上是关于计算机视觉中的深度学习6: 反向传播的主要内容,如果未能解决你的问题,请参考以下文章