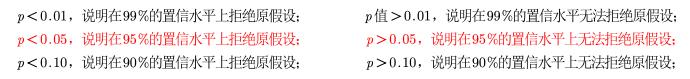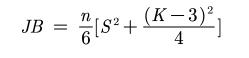相关系数之皮尔逊pearson相关系数和斯皮尔曼spearman等级相关系数(评价线性关系的相关系数)(第二部分)
Posted 衾许°
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了相关系数之皮尔逊pearson相关系数和斯皮尔曼spearman等级相关系数(评价线性关系的相关系数)(第二部分)相关的知识,希望对你有一定的参考价值。
前言
接上一部分的算出person相关系数了,接下来该干嘛呢?..
正常人会怎样,应该会去算相关系数可不可靠?那咋验算呢?
对皮尔逊相关系数进行假设检验(全是字,人都麻了)
第一步:提出原假设H0和备择假设H1,并且两个假设截然相反
假设我们计算出了一个person相关系数r,我们想检验它是否显著的异常于0,那么我们可以这样设定原假设和备择假设,H0:r = 0,H1:r !=0.
第二步:在原假设成立的条件下,利用我们要检验的量构造出一个符合某一分布的统计量,对于person相关系数r而言,在满足一定条件下,我们可以构造统计量
可以证明t是服从自由度为n-2的t分布
第三步:将我们要检验的这个值带入这个统计量中,可以得到一个特定的值(检验值)
假设我们计算出来的person相关系数是0.5,样本量为30,那我们就可以得到t=0.5*((30-2)/(1-0.5^2))^1/2 = 3.05505
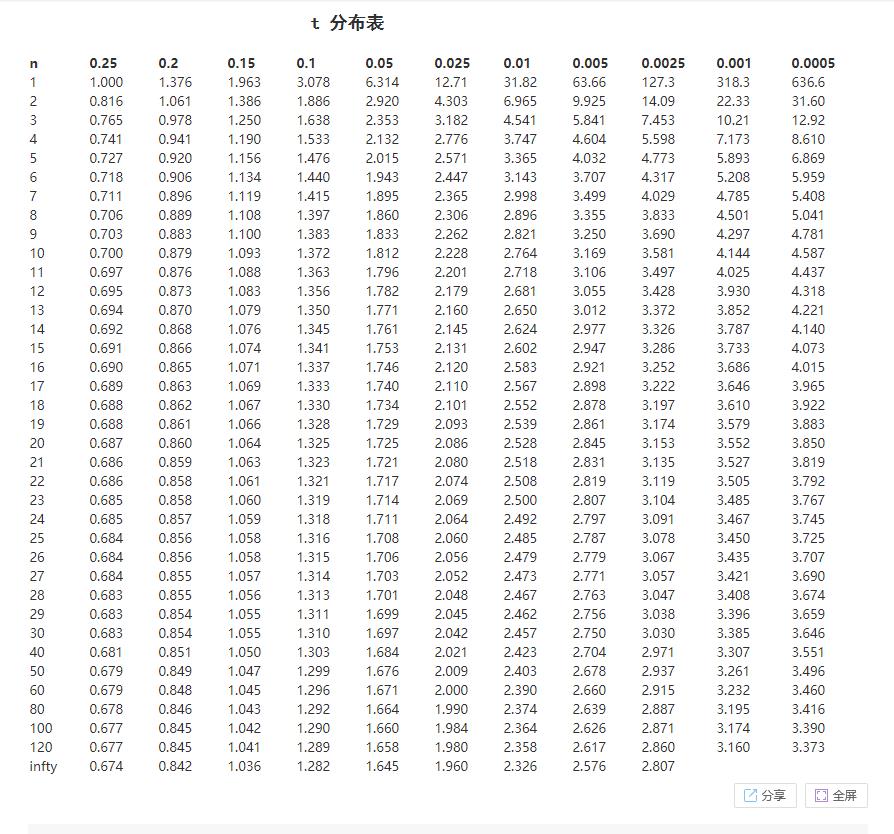
第四步:由于我们知道统计量的分布情况,因此我们可以画出该分布的概率密度函数pdf,并给定一个置信水平,根据这个置信水平表找到临界值,并画出检验统计量的接受域和拒绝域。
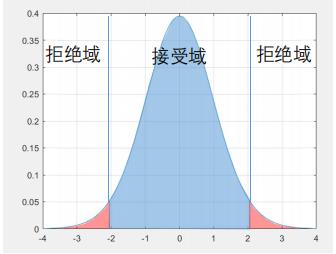
常见的置信水平有三个,0.9,0.95,0.99,一般都用0.95,我们可以通过查表找到对应自由度(样本量)的临界值,比如我们这个30样本的临界值就是2.042(双侧检验),根据临界值作图
第五步:根据我们计算出来的检验值是落在了拒绝域还是接受域,下结论。
模板:因为我们得到的t* = 3.05505>2.048,因此我们可以下结论:在95%的置信水平上,我们拒绝原假设H0:r = 0,因此r是显著的不为0的。
MATLAB代码(画图):
- %% 假设检验部分
- x = -4:0.1:4;
- y = tpdf(x,28); %求t分布的概率密度值 28是自由度
- figure(1)
- plot(x,y,'-')
- grid on % 在画出的图上加上网格线
- hold on % 保留原来的图,以便继续在上面操作
- % matlab可以求出临界值,函数如下
- tinv(0.975,28) % 2.0484
- % 这个函数是累积密度函数cdf的反函数
- plot([-2.048,-2.048],[0,tpdf(-2.048,28)],'r-')
- plot([2.048,2.048],[0,tpdf(2.048,28)],'r-')
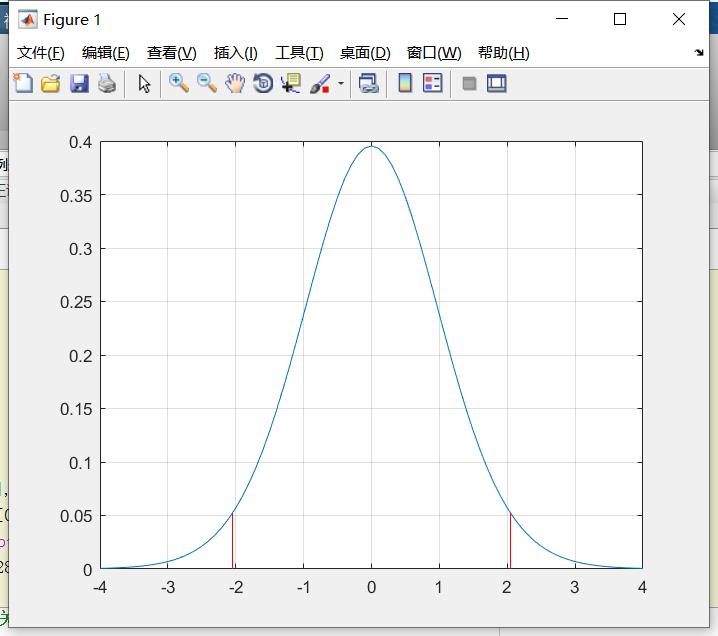
执行后图像
除了上面这个方法可以检验person相关系数外还有一种更好用的方法:
p值判断法
我们得到的检验值还是t = 3.05505哈,根据这个值,我们可以计算出对应的那个概率
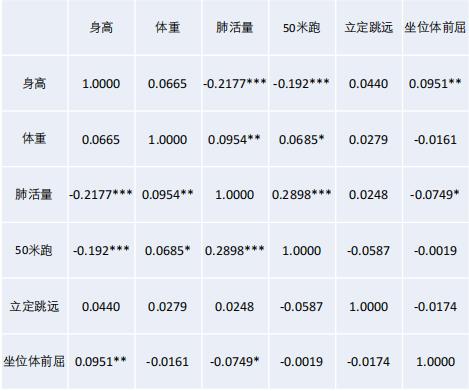
标星:*** p<0.01, ** p<0.05, * p<0.1
代码只有一行:
- %% 计算各列之间的相关系数以及p值
- [R,P] = corrcoef(Test)
- % 在EXCEL表格中给数据右上角标上显著性符号吧
- P < 0.01 % 标记3颗星的位置
- (P < 0.05) .* (P > 0.01) % 标记2颗星的位置
- (P < 0.1) .* (P > 0.05) % % 标记1颗星的位置
执行后
R =
1.0000 0.0665 -0.2177 -0.1920 0.0440 0.0951
0.0665 1.0000 0.0954 0.0685 0.0279 -0.0161
-0.2177 0.0954 1.0000 0.2898 0.0248 -0.0749
-0.1920 0.0685 0.2898 1.0000 -0.0587 -0.0019
0.0440 0.0279 0.0248 -0.0587 1.0000 -0.0174
0.0951 -0.0161 -0.0749 -0.0019 -0.0174 1.0000
P =1.0000 0.1061 0.0000 0.0000 0.2859 0.0208
0.1061 1.0000 0.0204 0.0960 0.4978 0.6963
0.0000 0.0204 1.0000 0.0000 0.5469 0.0687
0.0000 0.0960 0.0000 1.0000 0.1542 0.9637
0.2859 0.4978 0.5469 0.1542 1.0000 0.6728
0.0208 0.6963 0.0687 0.9637 0.6728 1.0000三颗星最好相关性最高,二星次之,dddd
三颗星的位置:0 0 1 1 0 0
0 0 0 0 0 0
1 0 0 1 0 0
1 0 1 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0两颗星的位置:
0 0 0 0 0 1
0 0 1 0 0 0
0 1 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1 0 0 0 0 0一颗星的位置:
0 0 0 0 0 0
0 0 0 1 0 0
0 0 0 0 0 1
0 1 0 0 0 0
0 0 0 0 0 0
0 0 1 0 0 0处理好后的表格
皮尔逊相关系数假设检验的条件
其实person相关系数假设检验也不是能够直接用的 第一, 实验数据通常假设是成对的来自于正态分布的总体。 因为我们在求皮尔 逊相关性系数以后,通常还会用 t 检验之类的方法来进行皮尔逊相关性系数检验, 而 t 检验是基于数据呈正态分布的假设的。 第二, 实验数据之间的差距不能太大。 皮尔逊相关性系数受异常值的影响比较 大。 第三:每组样本之间是独立抽样的。 构造 t 统计量时需要用到。 那问题又来了。。 如何检验正态分布呢?
正态分布JB检验(大样本 n>30)
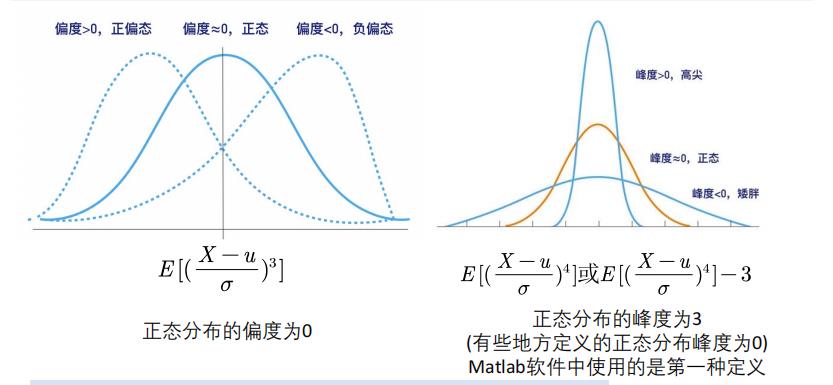
其实正态分布基本上就是又偏度和峰度两个值决定,若偏度和峰度都不太符合正态分布,所要求的条件,那便不可能为正态分布
对于一个随机变量Xi,假设其偏度为S,峰度为K,那么我们就可以构造JB统计量:
可以证明,如果Xi是正态分布,那么在大样本下JB~X^2(2)(自由度为2的卡方分布)
正态分布的偏度和峰度计算
- x = normrnd(2,3,100,1); % 生成100*1的随机向量,每个元素是均值为2,标准差为3的正态分布
- skewness(x) %偏度
- kurtosis(x) %峰度
- qqplot(x)
检验第一列数据是否为正态分布
- [h,p] = jbtest(Test(:,1),0.05)
- [h,p] = jbtest(Test(:,1),0.01)
用循环检验所有列的数据
MATLAB中进行JB检验的语法:[h,p] = jbtest(x,alpha) 当输出h等于1时,表示拒绝原假设;h等于0则代表不能拒绝原假设。 alpha就是显著性水平,一般取0.05,此时置信水平为1‐0.05=0.95 x就是我们要检验的随机变量,注意这里的x只能是向量。
- n_c = size(Test,2); % number of column 数据的列数
- H = zeros(1,6); % 初始化节省时间和消耗
- P = zeros(1,6);
- for i = 1:n_c
- [h,p] = jbtest(Test(:,i),0.05);
- H(i)=h;
- P(i)=p;
- end
- disp(H)
- disp(P)
Q-Q图
- qqplot(Test(:,1))
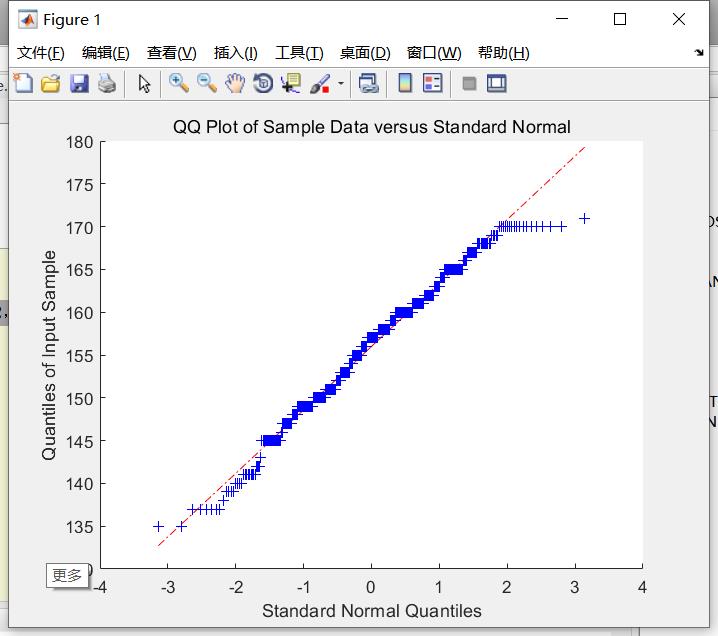
执行后:
关于QQ图
- 在统计学中,Q‐Q图(
- Q代表分位数Quantile)是一种通过比较两个概
- 率分布的分位数对这两个概率分布进行比较的概率图方法。
- 首先选定分位数的对应概率区间集合,在此概率区间上,点(x,y)对应
- 于第一个分布的一个分位数x和第二个分布在和x相同概率区间上相同的分
- 位数。
- 这里,我们选择正态分布和要检验的随机变量,并对其做出QQ图,
- 可想而知,如果要检验的随机变量是正态分布,那么QQ图就是一条直线。
小样本3≤n≤50:Shapiro-wilk检验
可以通过SPSS进行操作 斯皮尔曼spearman相关系数
斯皮尔曼spearman相关系数
斯皮尔曼相关系数和皮尔逊相关系数选择 : 1. 连续数据,正态分布,线性关系,用 pearson 相关系数是最恰当,当然用 spearman 相关系数也可以, 就是效率没有 pearson 相关系数高。 2. 上述任一条件不满足,就用 spearman 相关系数,不能用 pearson 相关系数。 3. 两个定序数据之间也用 spearman 相关系数,不能用 pearson 相关系数
斯皮尔曼相关系数计算
- X = [3 8 4 7 2]' % 一定要是列向量哦,一撇'表示求转置
- Y = [5 10 9 10 6]'
- % 第一种计算方法
- 1-6*(1+0.25+0.25+1)/5/24
- % 第二种计算方法
- coeff = corr(X , Y , 'type' , 'Spearman')
- % 等价于:
- RX = [2 5 3 4 1]
- RY = [1 4.5 3 4.5 2]
- R = corrcoef(RX,RY)
- % 计算矩阵各列的斯皮尔曼相关系数
- R = corr(Test, 'type' , 'Spearman')
- % 大样本下的假设检验
- % 计算检验值
- disp(sqrt(590)*0.0301)
- % 计算p值
- disp((1-normcdf(0.7311))*2) % normcdf用来计算标准正态分布的累积概率密度函数
- % 直接给出相关系数和p值
- [R,P]=corr(Test, 'type' , 'Spearman')
- X = [3 8 4 7 2]' % 一定要是列向量哦,一撇'表示求转置
- Y = [5 10 9 10 6]'
- % 第一种计算方法
- 1-6*(1+0.25+0.25+1)/5/24
- % 第二种计算方法
- coeff = corr(X , Y , 'type' , 'Spearman')
- % 等价于:
- RX = [2 5 3 4 1]
- RY = [1 4.5 3 4.5 2]
- R = corrcoef(RX,RY)
- % 计算矩阵各列的斯皮尔曼相关系数
- R = corr(Test, 'type' , 'Spearman')
- % 大样本下的假设检验
- % 计算检验值
- disp(sqrt(590)*0.0301)
- % 计算p值
- disp((1-normcdf(0.7311))*2) % normcdf用来计算标准正态分布的累积概率密度函数
- % 直接给出相关系数和p值
- [R,P]=corr(Test, 'type' , 'Spearman')
以上是关于相关系数之皮尔逊pearson相关系数和斯皮尔曼spearman等级相关系数(评价线性关系的相关系数)(第二部分)的主要内容,如果未能解决你的问题,请参考以下文章