[STL与数据结构]搜索二叉树
Posted 一个正直的男孩
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[STL与数据结构]搜索二叉树相关的知识,希望对你有一定的参考价值。
大家好呀!今天带来的文章是搜索二叉树,你是否在写题的时候遇到需要容器存储,且是否效率低下,没事搜索二叉(map,set的底层)树帮你解决问题

文章目录
搜索二叉树的底层结构
定义
搜索二叉树的
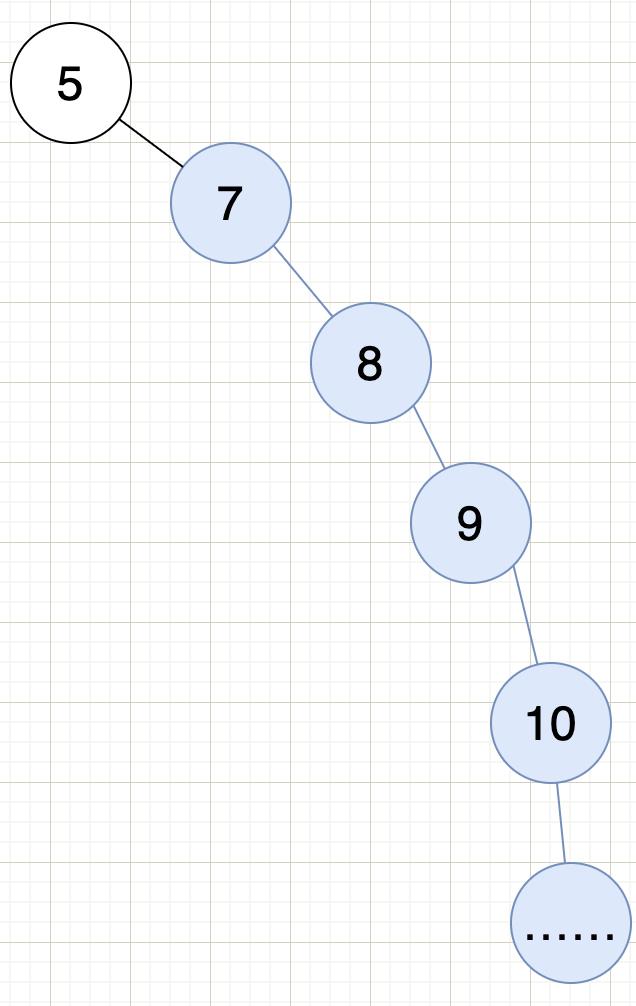
左子树永远比根小,右子树永远比根大,且树中值唯一确定(目前是),如图所示:

你仔细看发现每一棵子树都是按照那个规则的,你在仔细看如果按照
中序遍历(左,根,右)打印的话能会发现,竟然是一个升序的序列
问
那么这个用这个结构差找效率是多少呢?到底有多快呢?
答
搜索二叉的
效率的其实是O(N),这有点尴尬,其实一般情况就是高度次,因为在存入这个结构中的时候已经对半排开了,(所以这个比较看数据)最坏的情况如图所示:
造轮子理解底层
这样的数据结构一般涉及一下的接口
- 插入
- 删除
- 查找
问
为啥不是实现改的借口呢?这不是数据结构的四件套吗?
答
你仔细想想他这个结构可以改吗,上图第一张图所示,我把根改为0的时候,那这棵树不就不是搜索二叉了吗,数据不唯一,左子树的元素不比根小
二叉树节点与搜索二叉的基础结构
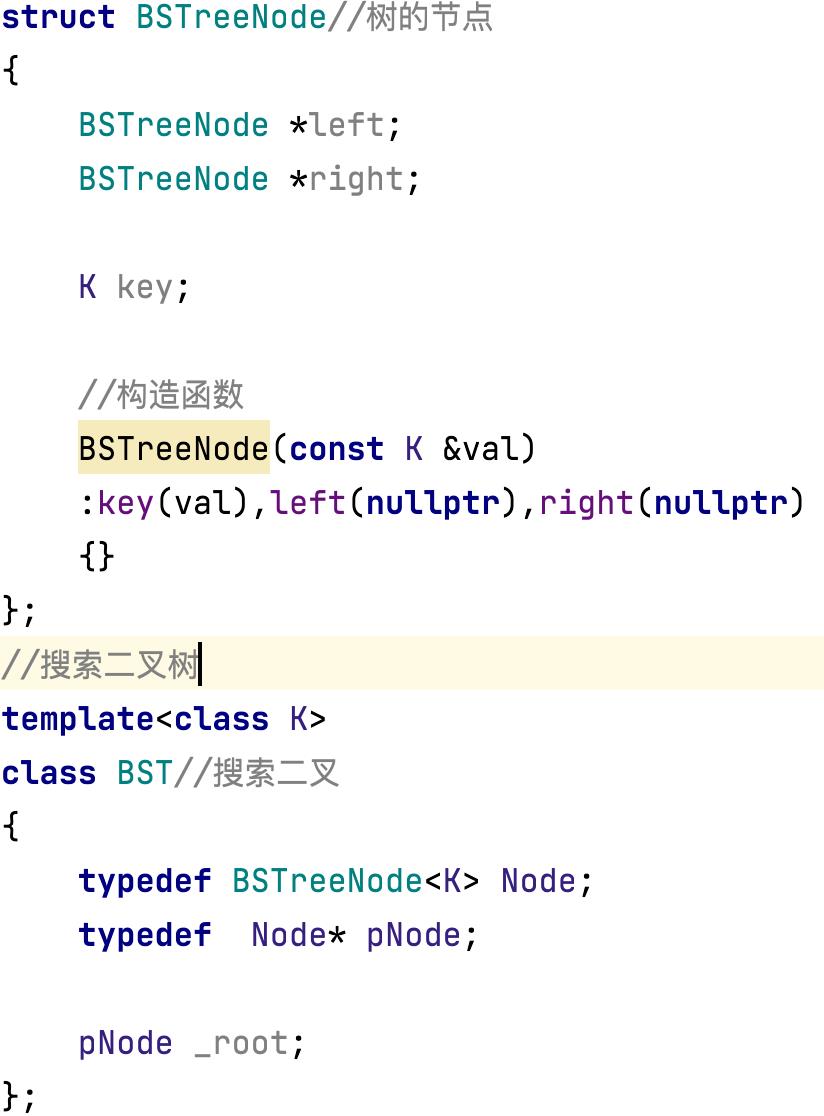
迭代版本
插入
当在插入实现的时候需要考虑一下几点
- 插入的时候是有节点(第一次插入)
- 插入那个位置
- 如何插入
代码:
bool Insert(const K &val)
if(_root==nullptr)//第一次插入没有节点的情况处理
_root =new Node(val);//构建节点
return true;
//寻找插入位置
pNode cur=_root;
pNode parent=nullptr;//
while(cur)
if(val<cur->key)//左子树
parent=cur;
cur=cur->left;
else if(val>cur->key)//右子树
parent=cur;
cur=cur->right;
//在判断数据的的大小那个位置方便插入
if(val<parent->key)
parent->left=new Node(val);
return true;
else if(val>parent->key)
parent->right=new Node(val);
return true;
//说明在树中已经有节点了
return false;
;
补充
上面第三个问题如何插入,这里采用用一个
前驱的父指针方便链接,如果单指针的话就会有链接不上的情况
查找
这里一块就是插入的简化板,只需要考虑如何找就可以了
pNode Find(const K&val)
pNode cur=_root;
while(cur)
if(val<cur->key)
cur=cur->left;
else if(val>cur->key)
cur=cur->right;
else
//找到了
return cur;
//这里就是没有找到
return nullptr;
删除
在进行删除的时候下面的情况要考虑
- 如何找到要删除的节点(显然上面已经实现过了)
- 如何删除
- 删除叶子结点
- 删除值有一个孩子的
- 删除俩个孩子的
如图所示:
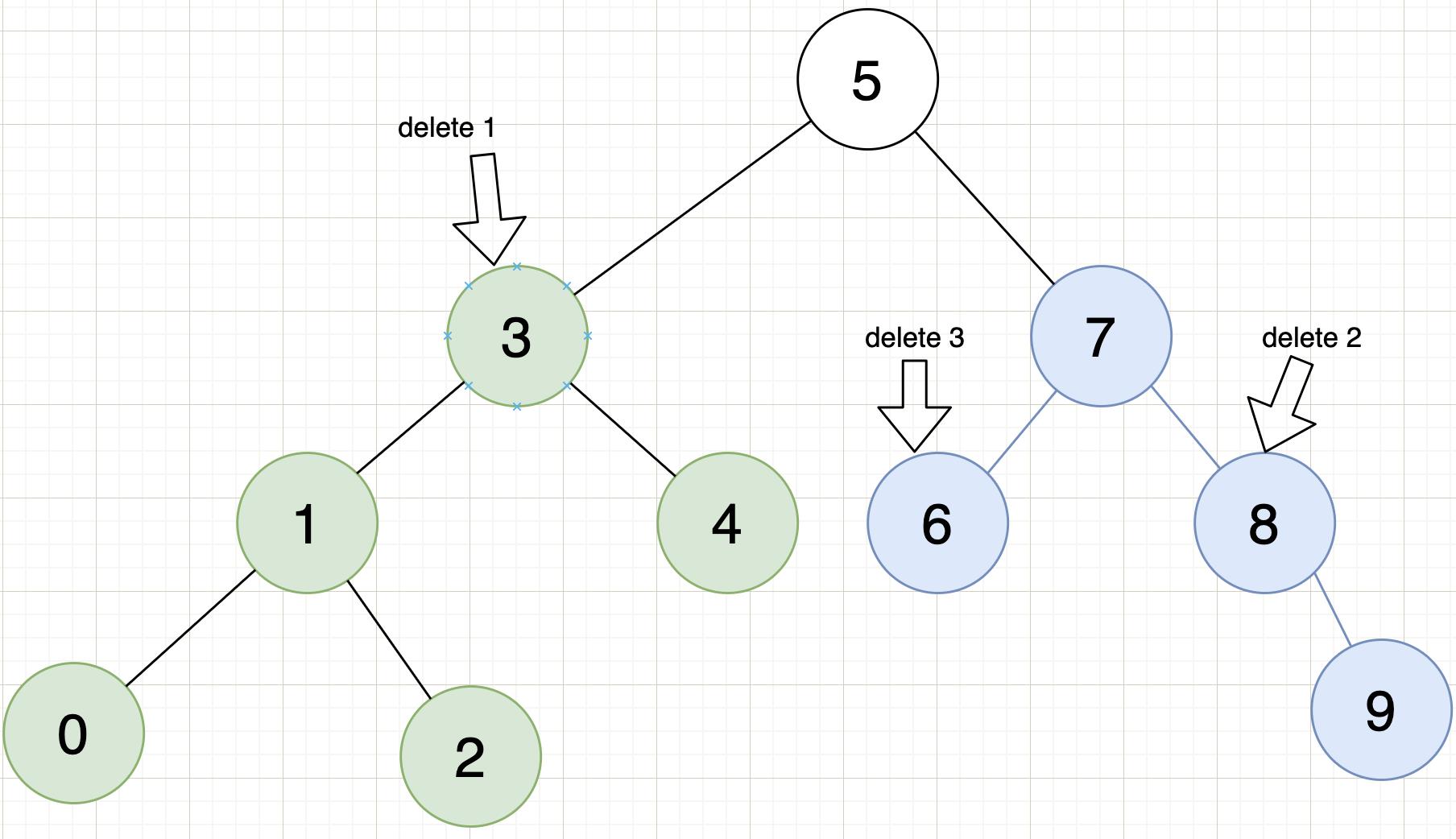
删除基本逻辑的代码
bool Erase(const K&val)
pNode parent=nullptr;//方便后续链接
pNode cur=_root;
//寻找节点
while(cur)
if(val<cur->key)
parent=cur;
cur=cur->left;
else if(val>cur->key)
parent=cur;
cur=cur->right;
else
//找到节点了
break;
//单个节点
//双个节点
delete cur;
//找不到的情况
return false;
第一二种情况分析如图所示:
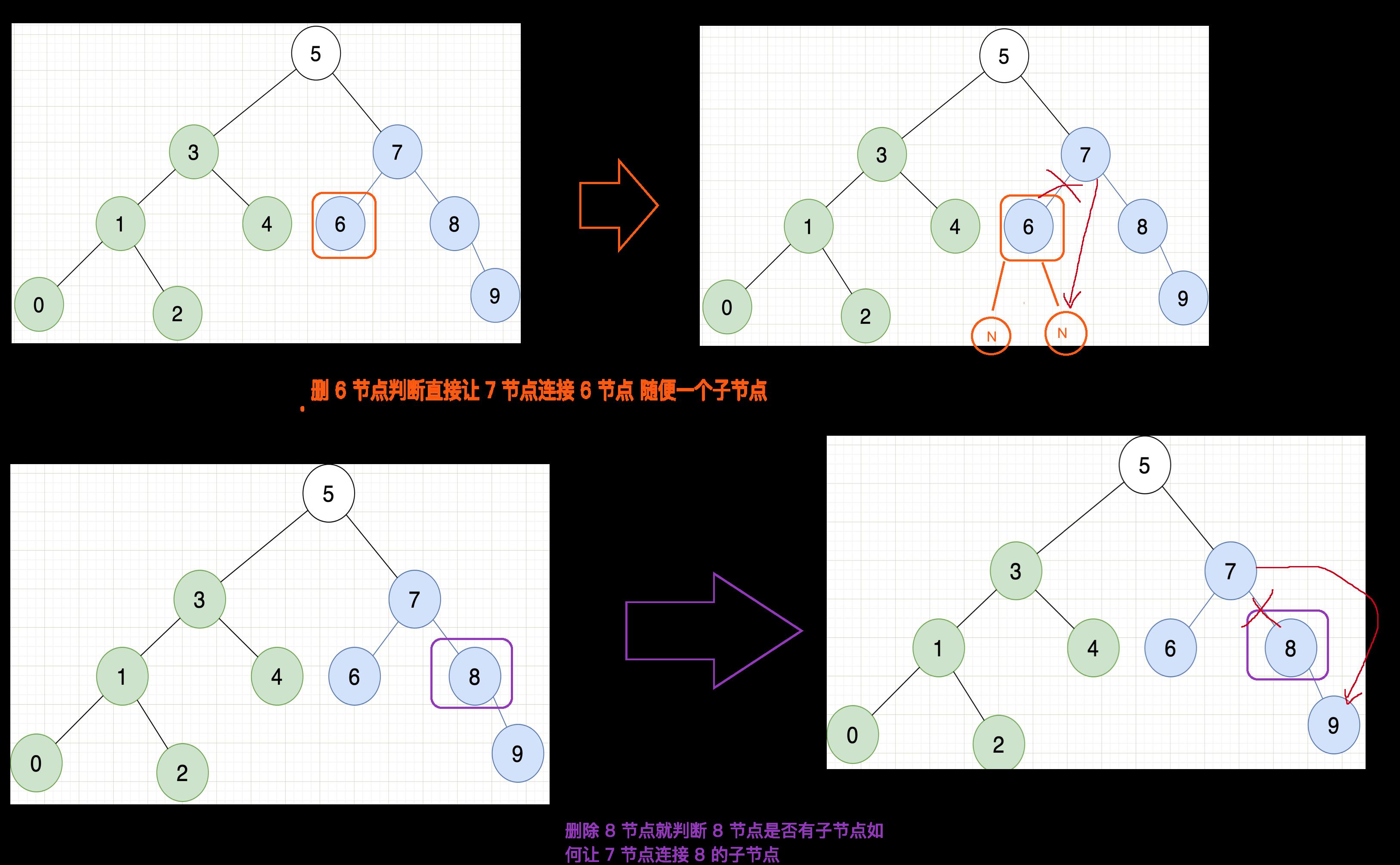
代码实现:
if(cur->right==nullptr||cur->left== nullptr)//直接包含了1,2俩个条件判断
if(cur->left!= nullptr)//特殊情况(画图处理)
_root=cur->left;
else
if(parent->left==cur)//判断链接的位置
if(cur->left!=nullptr)//判断删除的节点是否有子节点
parent->left=cur->left;
else
parent->left=cur->right;
else
//与上面逻辑同样
if(cur->left!=nullptr)
parent->right=cur->left;
else
parent->right=cur->right;
return true;//删除成功
补充
特殊情况就是这棵树删的是头节点,且只有单边的情况,这个时候就无法链接需要用新的方式,
直接改变头节点的指向如图所示:

情况三的分析图
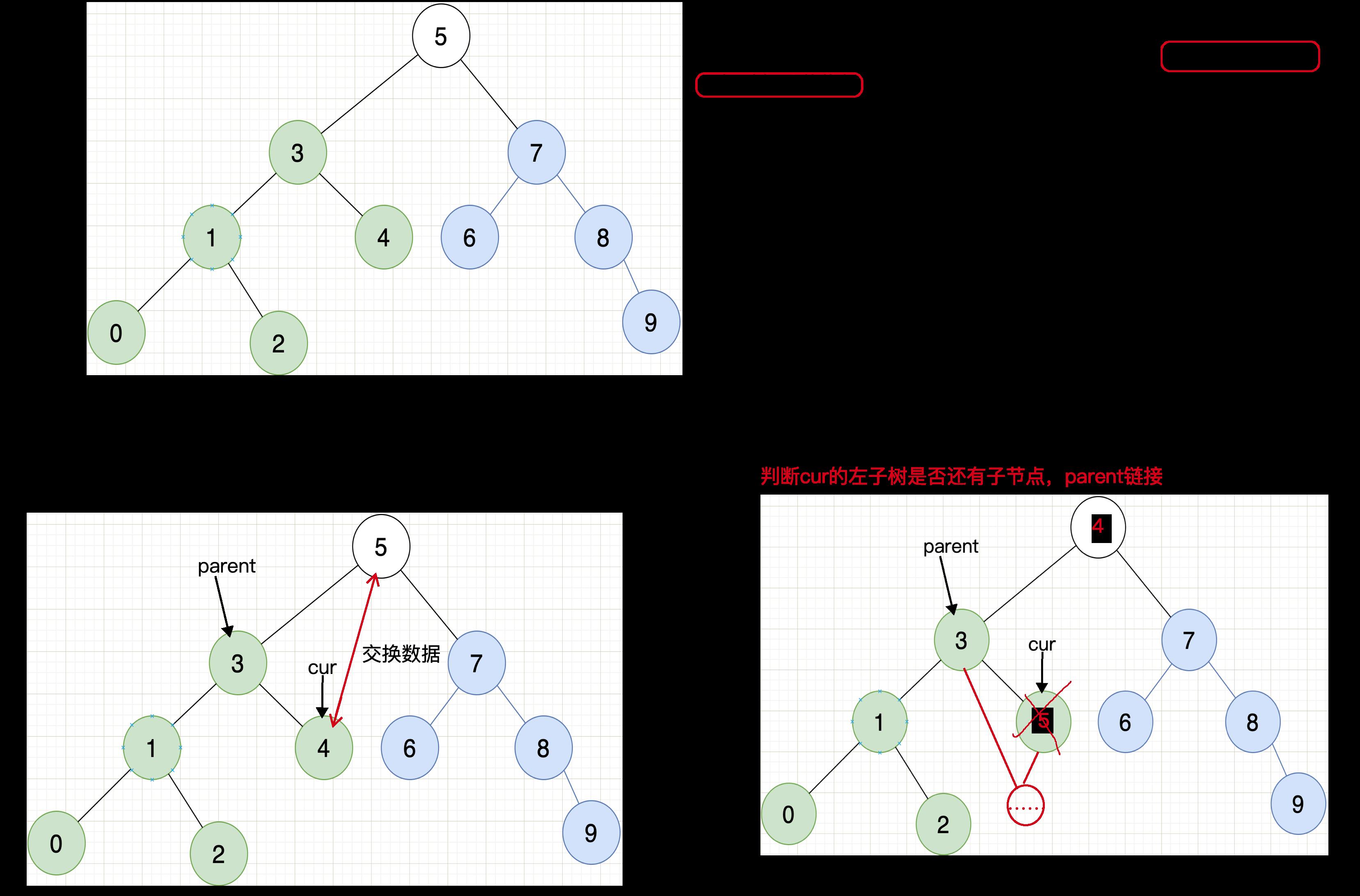
代码实现:
//删除俩个节点的情况
pNode DeVal =cur;//存的是要删除的节点
parent=cur;
cur=cur->left;
while(cur->right)//寻找左子树吧最大的节点
parent=cur;
cur=cur->right;
//交换数据
DeVal->key=cur->key;
//删除节点或许会剩下的节点,且判断链接位置
if(parent->left==cur)
parent->left=cur->left;
else
parent->right=cur->left;
return true;
中序遍历
void _Inorder(pNode cur)
if(cur==nullptr)
return ;
_Inorder(cur->left);
cout<<cur->key<<' ';
_Inorder(cur->right);
void InOrder()
_Inorder(_root);
;
问
为啥要实现俩个接口,你这不是在脱裤子放屁吗?
答
当在调用的时候_root是一个什么受什么限定符限制的
private(私有),那么就说明我在我是不可以访问的_root。那么解决方法一个我就是我这样写,还有一个方法就是把_root给暴露出来了(public),那么别人就可以随意破坏这个结构
递归版
插入
方法1
pNode construct(pNode cur,const K&val,int &de)
if(cur== nullptr)//插入的位置
return new Node(val);//构建节点返回
if(val<cur->key)//构建左子树
cur->left= construct(cur->left,val,de);
else if(val>cur->key)//构建右子树
cur->right= construct(cur->right,val,de);
else//有相同元素
de=0;
return cur;//返回当前节点
bool Insert(const K& val)
if(_root== nullptr)
_root=new Node(val);
return true;
int decide=1;
construct(_root,val,decide);
return decide;
方法2(引用法)
bool Construct(pNode &cur, const K& val)
if(cur==nullptr)//构造节点
cur=new Node(val);
return true;
if(val<cur->key)//递归左边
return Construct(cur->left,val);
else if(val>cur->key)//递归右边
return Construct(cur->right,val);
else//树中有相等的元素
return false;
bool Insert(const K& val)//插入
return Construct(_root,val);
方法1的写法是我想到递归法的第一反应的代码,看起来有一些冗余,方法2则干净明了就非常符合递归的宗旨,但是你或许都比较懵,那么就看下面的图解吧:
图解方法1,2:
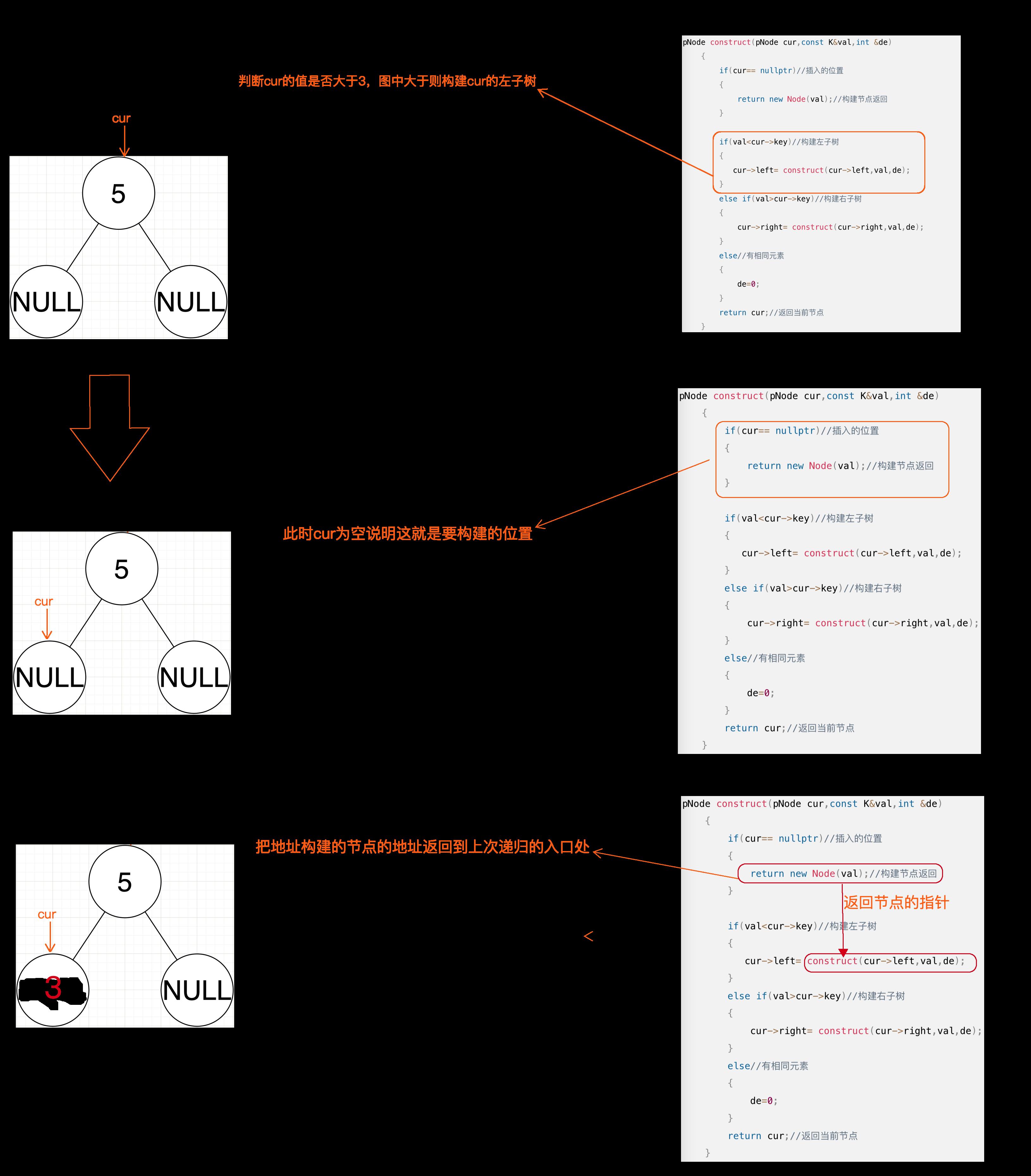
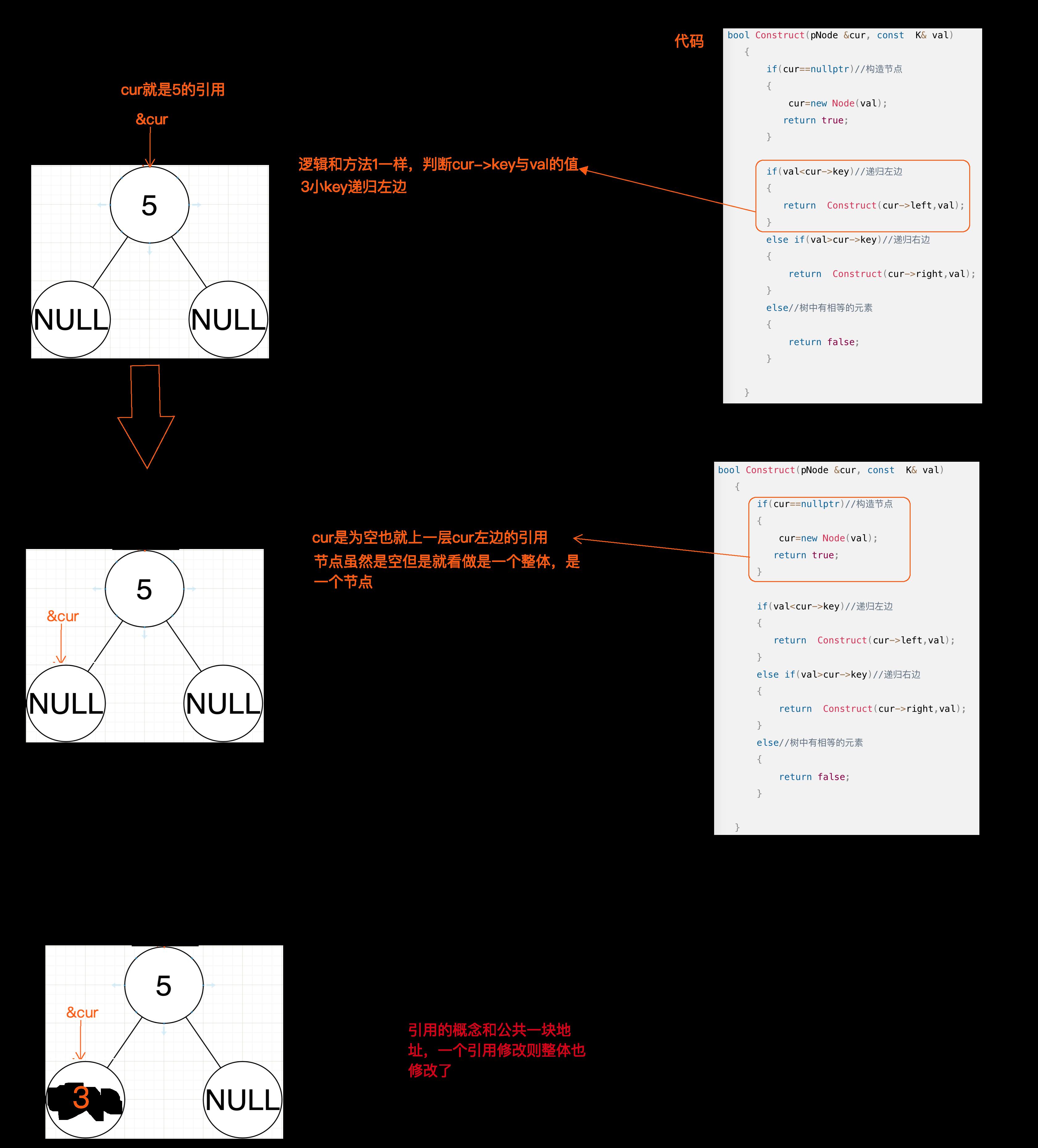
删除
bool _Erase(pNode& cur,const K&val)
if(cur==nullptr)
return false;
if(val<cur->key)
return _Erase(cur->left,val);
else if(val>cur->key)
return _Erase(cur->right,val);
else
pNode dele= cur;
//一个子节点
if(cur->left==nullptr)
cur=cur->right;
delete dele;
else if(cur->right==nullptr)
cur=cur->left;
delete dele;
else//俩个子节点
pNode parent=cur;
pNode cur2=cur->left;//这里不可以用cur迭代,因为那样就是赋值了
while(cur2->right)
parent=cur2;
cur2=cur2->right;
dele->key=cur2->key;
if(parent->left==cur2)
parent->left=cur2->left;
else
parent->right=cur2->left;
//如何删除cur这里的结构右链接不上了
//在递归一次
_Erase(cur2,cur2->key);
//删除节点
return true;
递归的删除其实没有啥好说的,其实就是在迭代版上改成递归了,删单个子节点和没有子节点的更方便,那为啥删双个的时候不行呢?根据迭代的思路,他是去找一个
替代节点替换值,在删除替换的节点如图:
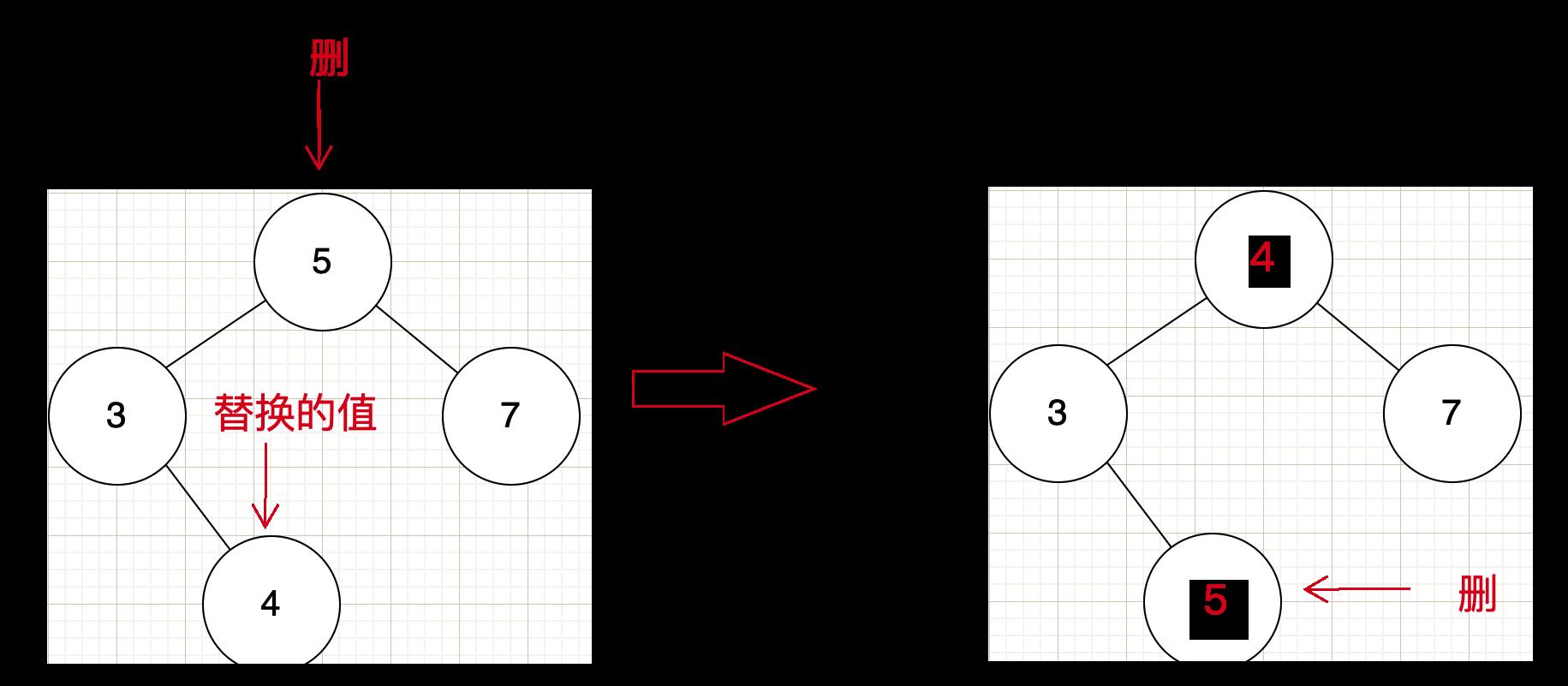
那么你觉得哪种实现方法比较好呢?
当然是迭代呀,
递归会有额外的内存消耗,如果树的层数太多就会栈溢出,虽然递归的代码短,这里要告诉你一个东西,一个程序的好坏不在与你写的代码有多短,而是看你的效率
搜索二叉树优化(key_val)
key_val这个结构真的随处可见如 买票,充会员,字典……
key_val的底层结构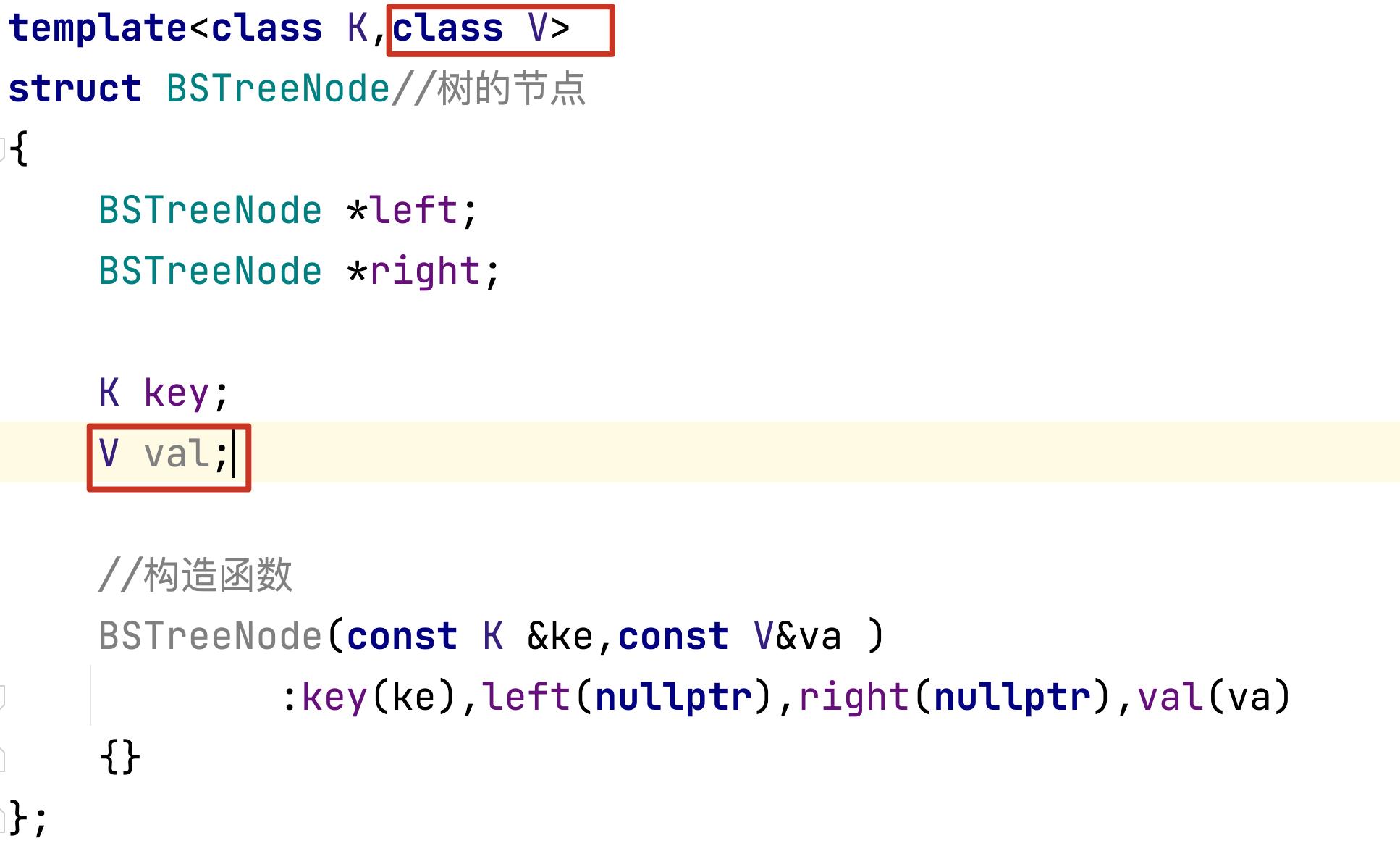
以字典为例子,
key就可以理解为单词,val就是翻译,所以key_val就是用于强相关的数据的结构
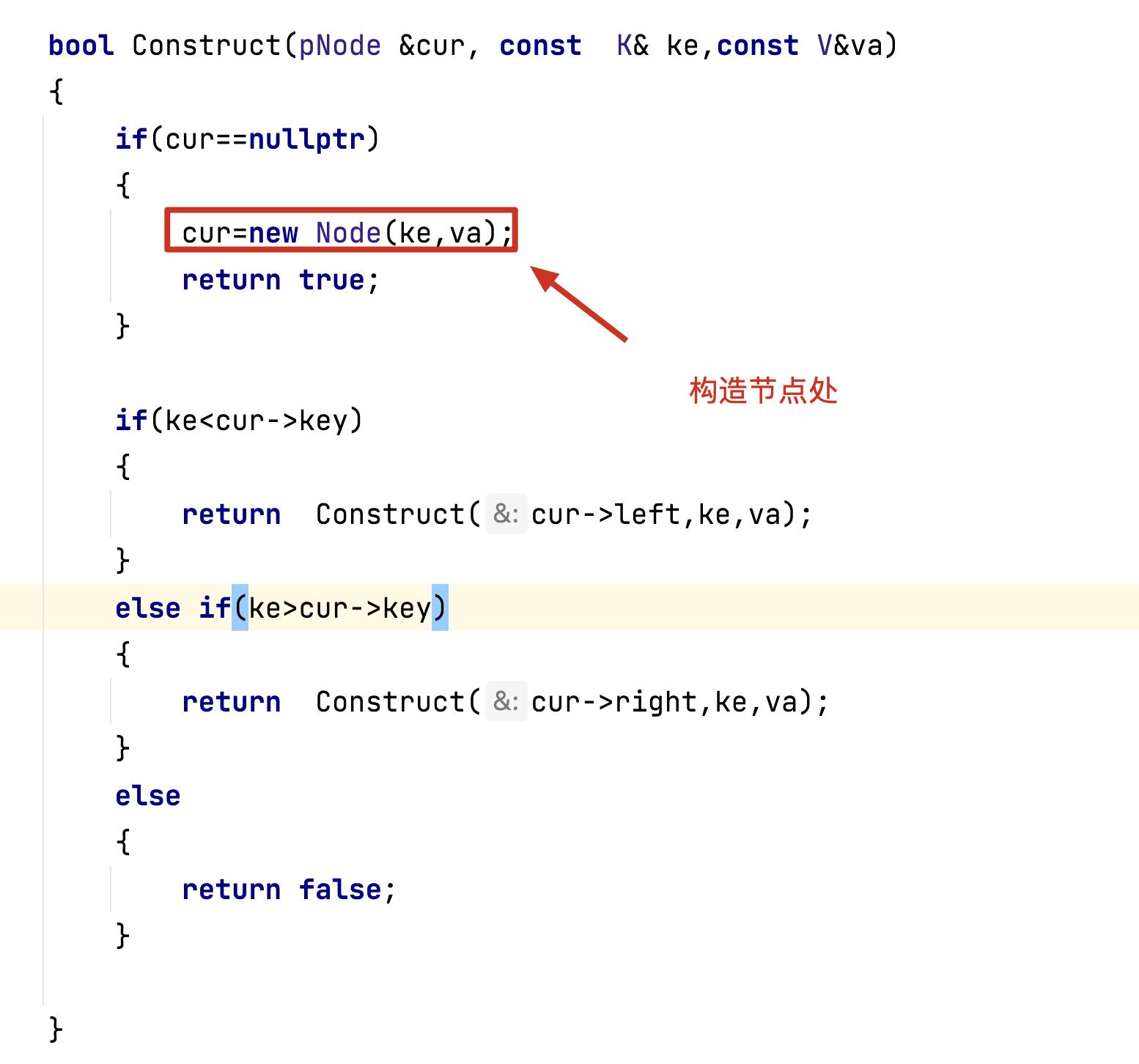
修改insert接口
只需要吧insert中全部构造节点的函数多加一个val的参数即可
刷题你或许写过这样的题

之前用暴力解法或者数组哈希映射,但是哈希写这样的还好,如果是字符串呢,且它还需要开对应的空间,会浪费,key_val(后续的map)就可以解决
代码:

set和map初步了解
在STL中set和与map的底层也是一个
‘’搜索二叉树‘’,但是优化过的,也就是平衡搜索二叉树,搜索二叉 就是set ,key_val就是map
唠唠家常
其实这是一个铺垫的文章,后面set,map都是以这个搜索二叉为出发点的,大致了解,学set,map就会轻松好多。。。那么就这样,谢谢观看我的文章

以上是关于[STL与数据结构]搜索二叉树的主要内容,如果未能解决你的问题,请参考以下文章