HDU 1402 A * B Problem Plus FFT+convert

Posted 2022-12-01 legend_PawN

HDU1402

两个大数的乘法
1.首先想到的用java Biginter类可以直接求，确实，比赛的时候肯定用java写这种简单的大数类的题目。
2.如果不用java的大数类，就会想到C++的bignumber模版，但是bignumber在进行乘法运算时也是每一位都要乘，然后再做加法，复杂度依旧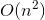大数的位数是50000，那么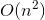的算法达到了10^9的复杂度，肯定会TLE
3.想到了FFT，两个整数的乘法为什么会想到FFT呢？
如果了解FFT的同学肯定知道整数的乘法和多项式的乘法在数学上是等价的，而多项式的乘法为了降低复杂度用的就是FFT，算法导论中的FFT讲也是基于多项式乘法的，将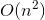的时间复杂度降低到了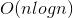，那么在50000的数据下这个算法是可行的。

如果不太了解FFT，我们也可以将数的乘法视为卷积，以123*123为例

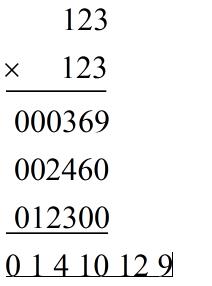
这是一般手算乘法的过程，下面得到的各位之和经过进位就到了最后的结果，实际上我们可以通过卷积得到:
卷积的具体工程大致如下:不妨设两个数组为a与b，首先翻转a数组，然后通过移动a数组与b数组相乘相加，就是卷积的结果，过程如下:

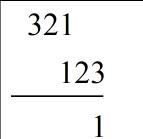
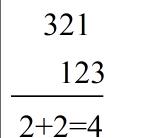
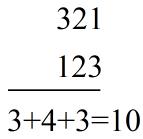
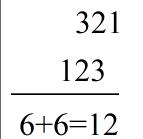
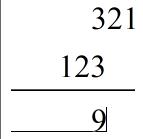
得到的结果 1 4 10 12 9就是乘法的结果。

最后如果进行卷积呢？那就要时域与频域转换了
时域卷积=频域乘积，所以我们计算卷积的过程就是
x1=DFT(a) //DFT就是离散傅里叶变换，把a转换到频域
x2=DFT(a)
x1=x1*x2 //时域卷积=频域乘积
x1=IDFT(a)，//IDFT离散傅里叶逆变换，再把x1从频域转化回来
这样就得到了卷积结果。
终于觉得自己学了两年的信号是有点用处的
看不懂了可以自行浏览大牛的FFT博客:
FFT,DFT,NTT

AC代码模仿bin神的模版

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn=200000+10;
const double PI=acos(-1);
char str1[maxn/2],str2[maxn/2];
struct complex
    double r,i;
    complex(double _r = 0.0,double _i = 0.0)
        r = _r; i = _i;
    
    complex operator +(const complex &b)
        return complex(r+b.r,i+b.i);
    
    complex operator -(const complex &b)
        return complex(r-b.r,i-b.i);
    
    complex operator *(const complex &b)
        return complex(r*b.r-i*b.i,r*b.i+i*b.r);
    
;
void change(complex y[],int len)
    int i,j,k;
    for(i=1,j=len/2;i<len-1;i++)
        if(i<j)
            swap(y[i],y[j]);
        k=len/2;
        while(j>=k)
            j-=k;
            k/=2;
        
        if(j<k)
            j+=k;
    

void fft(complex y[],int len,int on)

    change(y,len);
    for(int h=2; h<=len;h=h<<1)
        complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
        for(int j=0;j<len;j+=h)
            complex w(1,0);
            for(int k = j;k<j+h/2;k++)
                complex u = y[k];
                complex t = w*y[k+h/2];
                y[k]=u+t;
                y[k+h/2]=u-t;
                w=w*wn;
            
        
    
    if(on==-1)
        for(int i=0;i<len;i++)
            y[i].r/=len;

void convert(complex a[],complex b[],int len)
    fft(a,len,1);  //DFT
    fft(b,len,1);
    for(int i=0;i<len;i++)    //时域卷积=频域相乘
        a[i]=a[i]*b[i];
    fft(a,len,-1);//IDFT

complex x1[maxn],x2[maxn];
int main()
    //freopen("input.txt","r",stdin);
    while(~scanf("%s%s",str1,str2))
        int ans[maxn];
        int len1=strlen(str1);
        int len2=strlen(str2);
        int len=1;
        while(len<len1*2 || len<len2*2)
            len=len<<1;
        for(int i=0;i<len1;i++)
            x1[i]=complex(str1[len1-1-i]-'0',0);
        for(int i=len1;i<len;i++)
            x1[i]=complex(0,0);
        for(int i=0;i<len2;i++)
            x2[i]=complex(str2[len2-1-i]-'0',0);
        for(int i=len2;i<len;i++)
            x2[i]=complex(0,0);
        for(int i=0;i<len;i++)
            printf("%.0lf ",x1[i].r);
        cout<<endl;
        for(int i=0;i<len;i++)
            printf("%.0lf ",x2[i].r);
        cout<<endl;
        convert(x1,x2,len);
        for(int i=0;i<len;i++)
            ans[i]=int(x1[i].r+0.5);
            cout<<ans[i]<<" ";
        
        cout<<endl;
        for(int i=0;i<len;i++)
            ans[i+1]+=ans[i]/10;
            ans[i]%=10;
        
        len=len1+len2-1;
        while(ans[len]<=0 && len >0)
            len--;
        for(int i=len;i>=0;i--)
            printf("%c",ans[i]+'0');
        
        cout<<endl;