~小结论~

Posted 2022-11-29 thusloop

1+1/2+1/3+1/4+1/5+…………+1/n=ln(n)+C (C=0.5772156649)
gcd(lcm(a1,a2),lcm(a1,a3),lcm(a1,a4),…,lcm(a1,an))=lcm(a1,gcd(a2,a3,a4,…,an)
x+y=x|y+x&y
(a^ b)=(a&b)^(a|b)



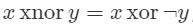
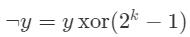
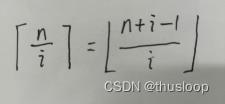
莫比乌斯反演

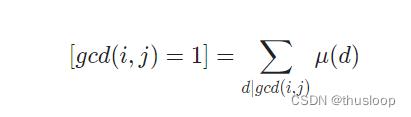
(l,r)区间lca是区间dfs序最大的点和区间dfs序最小的点的lca
最小循环节长度 n-Next[n] (kmp)
如果一个图不存在奇数环，那么一定是一个二分图

逆序对：1~n排列 奇数次交换任意2元素逆序对个数为奇，偶数次交换逆序对个数为偶；
交换相邻2元素使其有序的最小交换次数为逆序对个数

若 a%m=b%m 则(a-b)%m==0

长度至少为 5 的序列包含长度为 3 的非递减或非递增子序列

错排：f[1]=0;f[2]=1;f[i]=(i-1)(f[i-1]+f[i-2]);
卡特兰数 f[i]=f[i-1](4i-2)/(i+1) C(2n,n)-C(2n,n-1)
默慈金数 f[i]=((2i+1)f[i-1]+3(i-1)*f[i-2])/(i+2)

若gcd(a,b)=1,则 ax+by最大不能构成的数为a*b-a-b;
重构树： 原图中两个点之间的所有简单路径上最大边权的最小值 = 最小生成树上两个点之间的简单路径上的最大值 = Kruskal 重构树上两点之间的 LCA 的权值。

三角形面积：(xi,yi),(xj,yj),(xz,yz)

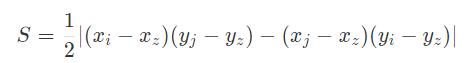
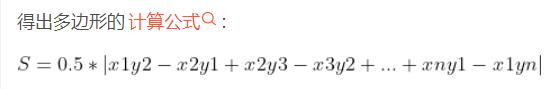
vector<int>().swap(v);//释放vector内存
v[x].insert(v[x].end(),v[it].begin(),v[it].end());//2个vector 合并

快速乘

int mul(int a,int b,int p)

	int x=(LD)a*b/p;//#define LD long double
	return ((a*b-x*p)%p+p)%p;//#define int long long

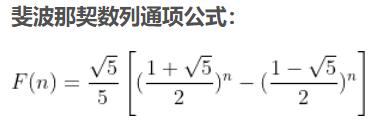
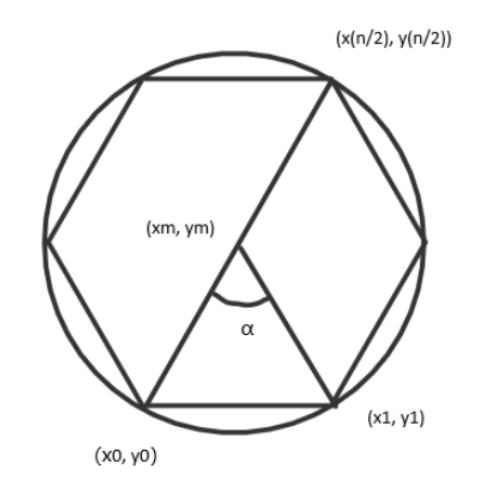
绕点的旋转公式：(例题：Opposite)
圆心（xm,ym）
x=(x0−xm)∗cos(a)−(y0−ym)∗sin(a)+xm
y=(x0-xm)∗sin(a)+(y0−ym)∗cos(a)+ym

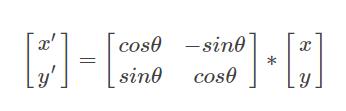
LGV (有向无环图)
A集合到B集合路径不相交的种类数
e(Ax,Bx) 为Ax到Bx的路径的种类数

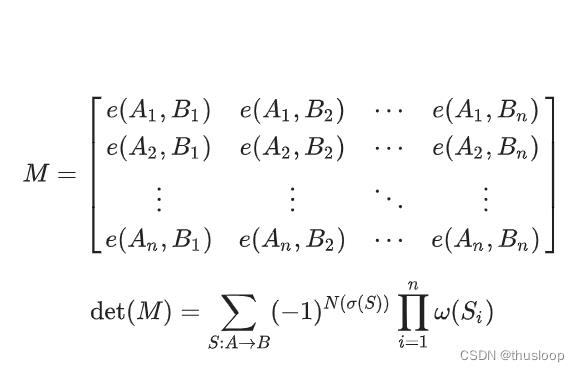
范德蒙行列式

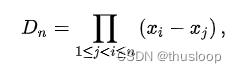
树状数组区间修改

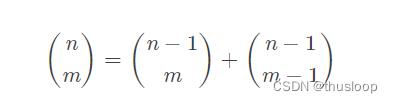
枚举子集

for (int j = x; j>=0; j = (j - 1) & x) 
        // j是x的子集
        if(j==0)break;

int128 输入输出

inline void read(__int128 &X)

	X = 0;
	int w=0; char ch=0;
	while(!isdigit(ch)) w|=ch=='-';ch=getchar();
	while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
	if (w) X = -X;

void print(__int128 x)

	if (!x) return ;//0特判
	if (x < 0) putchar('-'),x = -x;
	print(x / 10);
	putchar(x % 10 + '0');

        int **a;
		a=(int**)malloc(sizeof(int**)*(n+10));
		for(int i=0;i<=n+1;i++)
		
			aa[i]=(int*)malloc(sizeof(int)*(m+10));
		
		for(int i=0;i<=n+1;i++)
		for(int j=0;j<=m+1;j++)a[i][j]=0;