直观理解万能近似定理(Universal Approximation theorem)
Posted Jie Qiao
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了直观理解万能近似定理(Universal Approximation theorem)相关的知识，希望对你有一定的参考价值。
文本是教程"The Universal Approximation Theorem for neural networks" by Michael Nielsen 的笔记。
Universal approximation theorem
为什么MLP可以拟合任意的函数？
我们考虑一个最简单的神经网络，最后一层是sigmoid函数：
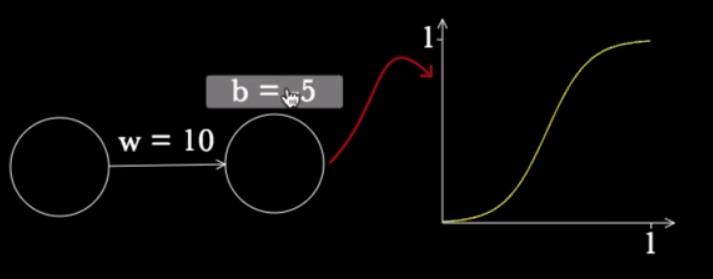
事实上这就是一个线性函数，然后经过sigmoid扭曲为一条曲线，显然，b决定了不同截距，从而导致sigmoid位置发生了平移。类似的，w决定了线的斜率，从而影响sigmoid倾斜程度：
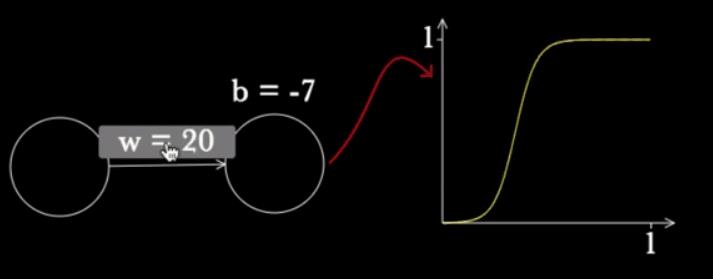
如果我们将斜率w设置为非常大，那么这个sigmoid函数将成为一个分段函数：
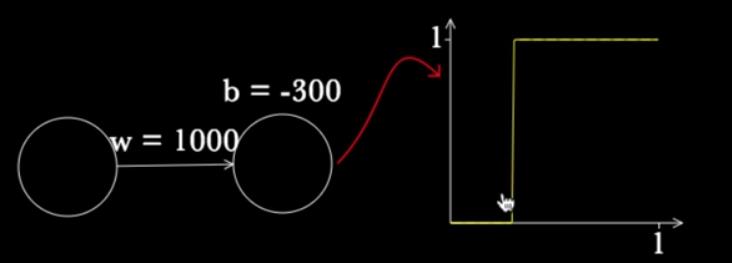
如果熟悉决策树的话，其实已经可能有同学猜到这个分段函数怎么去近似任意的函数了，其实很直接，我们可以构造很多个不同的分段函数：
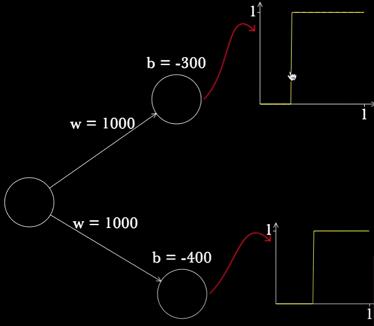
然后将他们以某种权重相加，就能得到一条经过两次分段的函数：
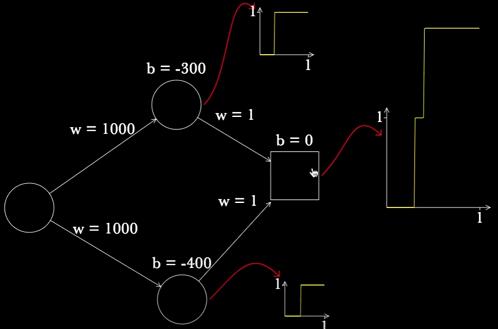
只要我们有足够多的分段函数，并且仔细调整他们相加的权重，我们就能近似任意的函数：
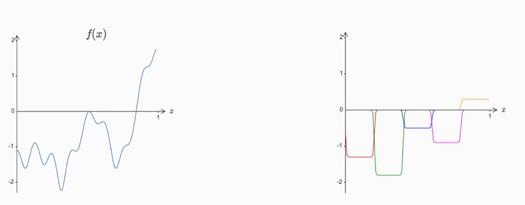
在多维函数也是类似的，只是变成一种对空间的划分，只要划分足够多，总能近似任意的函数。
参考资料
Understanding the Universal Approximation Theorem
The Universal Approximation Theorem for neural networks
以上是关于直观理解万能近似定理(Universal Approximation theorem)的主要内容，如果未能解决你的问题，请参考以下文章
直观理解万能近似定理(Universal Approximation theorem)
机器学习笔记：MLP的万能逼近特性（ Universal Approximation Property）
机器学习笔记：MLP的万能逼近特性（ Universal Approximation Property）