梦开始的地方 —— C语言数据在内存中的存储(整形+浮点型)
Posted 爱敲代码的三毛
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了梦开始的地方 —— C语言数据在内存中的存储(整形+浮点型)相关的知识,希望对你有一定的参考价值。
文章目录
整形在内存中的存储
1. 数值类型的基本分类
整形家族
默认不写signed也是也是有符号的数字,无符号的数字表示没有负数
char
signed char //有符号的char
unsigned char //无符号的
short
signed short
unsigned short
int
signed int
unsigned int
long
signed long
unsigned long
long long
signed long long
unsigned long long
来看一段代码
这段代码输出的是大于,这是为什么呢?
#include <stdio.h>
#include <string.h>
int main(void)
char* str1 = "1234567";
char* str2 = "12345";
if (strlen(str2)-strlen(str1) < 0)
printf("小于");
else
printf("大于");
return 0;
通过查看函数定义发现strlen的返回类型是size_t,而size_t本质上就是我们的unsigned int类型,也就是无符号整数,无符号数是没有负数的所以是不可能小于0的。
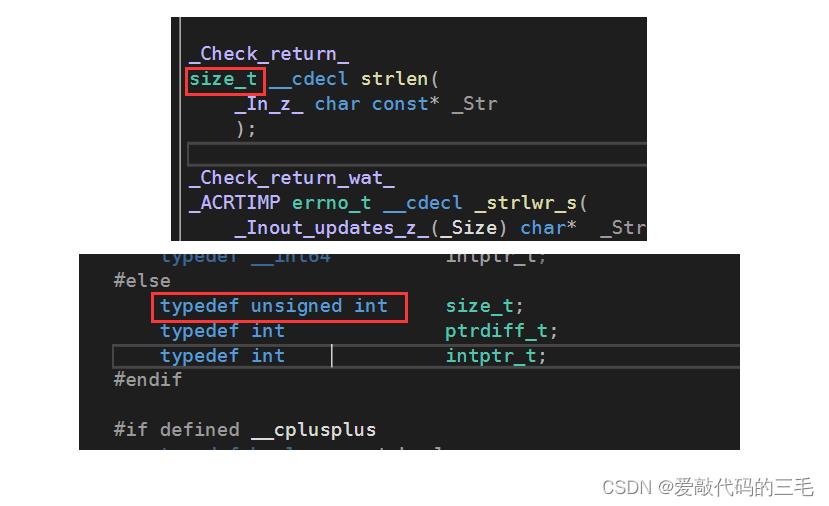
2. 整形在内存中的存储
1. 原码、反码、补码
我们知道创建变量就会在内存开辟空间,不同类型的变量所占的空间也不同。
那么数据在内存中到底是如何存储的呢?
我们得先来了解一下什么是原码、反码补码。
在计算机中有符号数有三种表示方法,分别是原码、反码、补码,三种表示方法都有符号位(0表示正数,1表示负数),和数值位位组成,数值位的表示方式各部相同
正数的原反补相同。
- 原码:将一个数字直接转换为二进制对应的二进制,最高位是符号位。
- 反码:将原码的二进制位除了符号位以外的数值位都按位取反,得到的就是反码
- 补码:将反码加一得到的二进制位就是补码
对应整形来说存放在内存中的就是补码
来简单看一下
int a = 10;
int b = -20;
我们知道正数的原码反码和补码都相同
10的二进制位就是:00000000000000000000000000001010
把这个二进制转换为十六进制就是0xa
在VS2019监视内存就是以十六进制表示的,可以看到上面的图片中就是存放的就是0a也就十进制的10
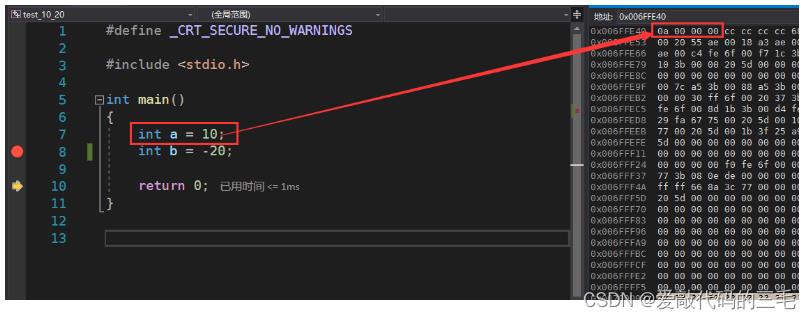
我们再来看一下 变量b存的是**-20**,负数在内存中存储的是补码
-20转换为二进制位得到原码
- 原码:
10000000000000000000000000010100,最高位符号1表示这是一个负数 - 反码:
11111111111111111111111111101011,原码除符号位以外取反得到反码 - 补码:
11111111111111111111111111101100,反码+1得到补码
在内存中存的就是补码,把这个补码转换为16进制,就可以得到我们在VS监视内存中的那个值FFFF FFEC
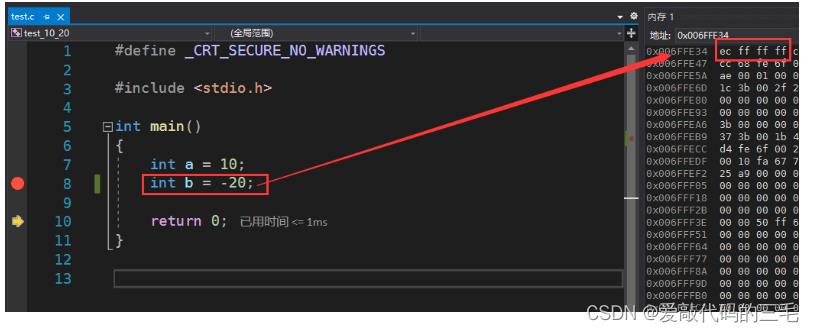
2. 内存中为什么要存放补码?
为什么负数在内存中要存放补码,而不直接存放原码呢?这可定是有原因的。
因为CPU它只有加法器,只能运算加法而不能运算减法,使用补码可以将符号位和数值位同一处理。在计算机系统中数值一律用补码存储和表示。
举个列子我们要算一个简单的正负数加减去
int a = -1;
int b = 1;
int tmp = b + a;
如果b+a用补码来计算,我们本能反映是1-1这么计算的,但CPU没有加法器,他是 1+(-1)这么计算的
a是个负数所以要先知道它的补码
a的原码:10000000000000000000000000000001
a的反码:11111111111111111111111111111110
a的补码:11111111111111111111111111111111
b的原反补:00000000000000000000000000000001
将它们相加
11111111111111111111111111111111
00000000000000000000000000000001
100000000000000000000000000000000
因为int只有4个字节32个比特位,所以它们的最高位是存不下的就把截断了。最后结果就是0
如果通过原码来计算,显然是没法计算的
a的原码:10000000000000000000000000000001
b的原码:00000000000000000000000000000001
相加:10000000000000000000000000000010
计算出来是**-2**?,显然这是不合理的
所以把补码存在内存中是为了更方便的进行计算
3. 大小端存储
我们刚刚看到VS2019中的内存监视,发现存储的16进制的顺序有点不对劲?这是啥情况?
这就涉及到端和小端存储了
-
大端字节序存储
把以数据的低位字节的内容,放在高地址处。高位字节的内容,放在低地址处。
-
小端字节序存储
把一个数据的低位字节的内容,存放在低地址处。高位字节的内容,存放在高地址处。
我们来看一下我的系统是win10,在vs2019中查看是大端还是小端
我们定义一个整形变量a,存放十六进制的0x11223344,从左到右一次是高位到低位。
而我们在vs2019中调试查看内存,它的地址是从低到高增长的。那就把低位的字节存放到了低地址处,高位的字节存放到了高地址处。那么我这台机器就是小端存储
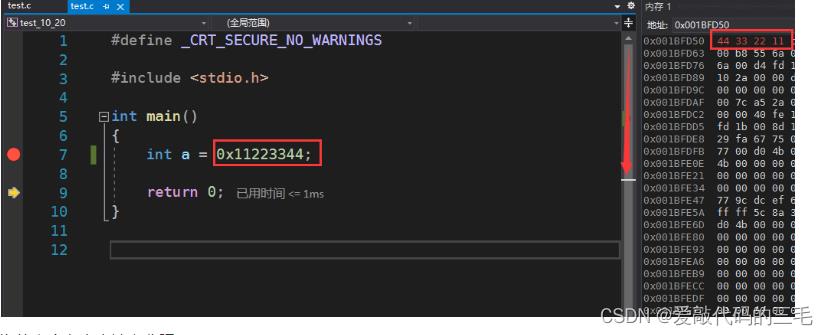
为什么会有大小端之分呢?
因为在计算系统中是以字节为单位的,每个地址单元都对应着一个字节,一个字节是8个比特位,但是C语言中有很多不同的类型,所占的内存空间不一样,不同的CPU的寄存器大小也不一样,就出现了字节存放顺序的按排问题,所以大端存储和小端存储就由此而来。
如何通过代码来判断机器是大端字节序还是小端字节序?
定义一个整形变量a存放的是1
取出a的地址放到一个char类型的指针里去,我们知道char类型的指针解引用只拿到低地址的一个字节
如果是小端解引用显然就会拿到数字1
而如果是大端,低位字节会放到高地址处,那么解引用是拿不到1的。拿到的就会是0
#include <stdio.h>
int main()
int a = 1;
char* p = (char*)&a;
if (*p == 1)
printf("小端\\n");
else
printf("大端\\n");
return 0;
4. 无符号有符号数练习
来看一段代码,这个代码输出:a=-1,b=-1,c=255
#include <stdio.h>
int main()
char a= -1;
signed char b=-1;
unsigned char c=-1;
printf("a=%d,b=%d,c=%d",a,b,c);
return 0;
这是为什么?
-1是整形又是负数,它在内存中存的是补码
原码:10000000 00000000 00000000 00000001
反码:11111111 11111111 11111111 11111110
补码:11111111 11111111 11111111 11111111
把补码存进去,而char只有一个字节8个比特位,就会发送截断
此时a里面存的就是11111111,a是一个有符号数,而这个数字是一个补码要把它转换为原码
补码:11111111
反码:11111110
原码:10000001
得到的就是-1,而signedc char 和char 是等价的都是有符号的字符类型所以它们都是-1
最关键的地方来了,就是变量c,同样-1是一个有符号的执行它的
原码:10000000 00000000 00000000 00000001
反码:11111111 11111111 11111111 11111110
补码:11111111 11111111 11111111 11111111
由于char是一个字节8个比特位,所以会发送截断最后存放的是 11111111
而c是一个无符号的char,意味着它是没有符号位的。有符号数的最高位是符号位,而无符号数的最高位也是数值位。无符号数原码补码反码是相同的,所以在变量c里存放的就是11111111。在printf打印的时候发送整形提升,无符号数提升的是0,所以打印出来的就是255
继续来看一段代码
这段代码打印4294967168
#include <stdio.h>
int main()
char a = -128;
printf("%u\\n",a);
return 0;
同样 -128是一个整形有符号数,把它的原反补写出来
原码:10000000 00000000 00000000 10000000
反码:11111111 11111111 11111111 01111111
补码:11111111 11111111 11111111 10000000
因为a只有一个字节,此时就会发送截断,所以a里面存的是补码 10000000
此时要以 %u的形式打印,打印的是整数。
打印整形此时就会发送整形提升,而char是一个有符号数就会以高位的符号位来进行提升
11111111 11111111 11111111 10000000 ,这就是整形提升后的补码存放的内存中。
而%u虽然是打印整形但它打印的是无符号的整形,所谓无符号整形是它认为内存中存的是无符号数。
所以它认为 11111111 11111111 11111111 10000000 就是一个无符号数,而无符号数的原反补都相同
所以最后直接打印出的是4294967168,转换为二进制就是
11111111 11111111 11111111 10000000
再来看一段代码
#include <stdio.h>
int main()
char a = 128;
printf("%u\\n",a);
return 0;
128是一个整形,但它是一个正数,正数的原码反码补码都相同
那在内存中存的就是:00000000 00000000 00000000 10000000
而char只有一个字节所以这个二进制放到变量a中会发送截断
所以a里面存放的就是 10000000
此时以%u打印,打印的是整形,就又会发生整形提升,而char是一个有符号数以最高位的符号位来提升
提升成:11111111 11111111 11111111 10000000
提升完后是以补码存放在内存中,而以%u打印的是无符号的整形,所谓的无符号整形,是它认为你在内存中存放的补码就是一个无符号数,所以它直接打印的就是
11111111 11111111 11111111 10000000的十进制4294967168
下一个列子
#include <stdio.h>
int main()
int i = -20;
unsigned int j = 10;
printf("%d\\n", i + j);
这个列子比较简单,unsigned int其实就是一个正整数,就是简单的**-20+10最后打印-10**
继续看这么一段代码:下面这段代码是一个死循环
#include <stdio.h>
int main()
unsigned int i;
for (i = 9; i >= 0; i--)
printf("%u\\n", i);
打印的
9
8
7
6
5
4
3
2
1
0
4294967295 无符号整形的最大值…
从上面一次递减每次到了0在减减,因为 变量i 是一个无符号数,没有负数所以每次0减一就会变成 无符号整形的最大值4294967295 ,在从最大值减到 9 8 7 6 5 4 3 2 1 0 又回到了无符号的最大值,就出现了死循环
下一个列子,最后打印的应该是255
#include <stdio.h>
int main()
char a[1000];
int i;
for(i=0; i<1000; i++)
a[i] = -1-i;
printf("%d",strlen(a));
return 0;
我们知道char是一个有符号数占一个字节,它能表示的数据范围是 -128~127
下面图是内存中的补码

循环走下来,一次是 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 …
到-128的时候内存里其实存的是 10000000,其实这个值是不好算的这个补码会直接转换成-128
那当i等于128的时候,此时 -1 - 128 就是 -129 ,那么来看一下-129的原反补码
原码:10000000 00000000 00000000 10000001
反码:11111111 11111111 11111111 01111110
补码:11111111 11111111 11111111 01111111
此时char只有一个字节只能存8个比特位,发生截断就是 01111111
char是一个有符号数,它的符号位是0也就是一个正数,正数的原反补都相同
所以此时存放的就是01111111,也就是127
所以把-129存到一个char类型的变量中,他其实存的是 127
同样那么把-130存放到char里
原码:10000000 00000000 00000000 10000010
反码:11111111 11111111 11111111 01111101
补码:11111111 11111111 11111111 01111110
发生截断后变成 01111110,存的就是 126
依此类推那么就是 ,127,126,125 … 1,0
到0的时候,我们知道
\\0的ASCII码值也是0,后面的就可以先不管了。strlen这个函数只要读取到
\\0它就不会往后计算了,切\\0也不包含在长度范围内那么从-1到-128,再从127到1一共是有255个数字
所以最后的结果是 255
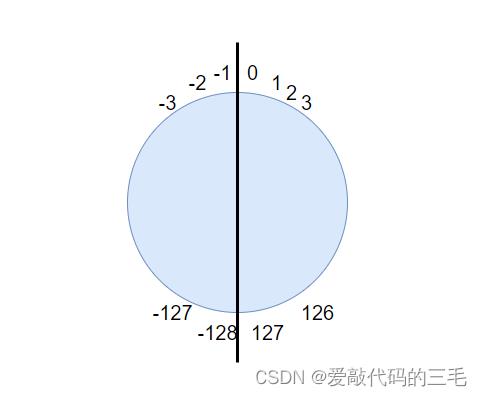
所以可以得出的是 0,1,2,3,4,…,127,-128,-127,-126,-125,…,0,1,2,3,4,5
有符号的char能表示的最大正数是127,把127+1放到char里就变成了char能表示最小的负数
同理把char能表示的最小负数-128减去一个1就会变成char能表示的最大正数127
5. 有符号数无符号数小结
在#include <limits.h>这个头文件下定义了整型家族的最大最小值
简单来看一下
//有符号字符形和无符号字符形能表示的最大值和最小值
#define CHAR_BIT 8
#define SCHAR_MIN (-128)
#define SCHAR_MAX 127
#define UCHAR_MAX 0xff
//有符号整形和无符号整形能表示的最大值
#define INT_MAX 2147483647
#define UINT_MAX 0xffffffff
有符号char的范围是**-128到127**,无符号char表示的范围是0到255
而有符号Int能表示的最大数是2147483647,无符号能表示的最大数字是0xffffffff,转换为十进制就是 4,294,967,295
无符号数没有负数,但它最大能表示的数都要比有符号数大。
浮点型在内存中的存储
浮点型家族
float
double
long double //有些编译器不支持
浮点型型的标识范围在float.h头文件中定义
来看一段代码
#include <stdio.h>
#include <float.h>
int main()
int a = 6;
float* f = (float*)&a;
printf("%d\\n", a);
printf("%f\\n", *f);
*f = 6.0;
printf("%d\\n", a);
printf("%f\\n", *f);
return 0;
这段代码再VS2019的X64平台输出为
6
0.000000
1086324736
6.000000
这是为啥???
a和*f在都是存储在内存中,而通过浮点数和整数的读取结果这么出乎意料。要想了解为什么,就了解浮点数在内存中的存储
IEEE 754
IEEE二进制浮点数算术标准(IEEE 754)
根据IEEE754标准规定,任意一个二进制浮点数V可以表示成下面的形式
- ( − 1 ) S ∗ M ∗ 2 E (-1)^S * M * 2^E (−1)S∗M∗2E
- ( − 1 ) S (-1)^S (−1)S 表示符号位,当 S = 0 S=0 S=0时,V为正数,当 S = 1 S=1 S=1时,V为负数
- M用来表示有效数字位, 1 ≤ M < 2 1\\leq M<2 1≤M<2
- 2 E 2^E 2E表示指数位
举个列子:
十进制的6.5,写成二进制就是110.1,注意这里是二进制不是十进制。所以0.5用0.1表示。
再把110.1用科学计数法表示 就是
1.101
∗
2
2
1.101 * 2^2
1.101∗22,那么按照上面V的格式就可以得出
- S = 0 S=0 S=0
- M = 1.101 M=1.101 M=1.101
- E = 2 E=2 E=2
- ( − 1 ) 0 ∗ 1.101 ∗ 2 2 (-1)^0 * 1.101 * 2^2 (−1)0∗1.101∗22
如果是 -6.5那么用V的格式来表示就是
- ( − 1 ) 1 ∗ 1.101 ∗ 2 2 (-1)^1 * 1.101 * 2^2 (−1)1∗1.101∗22
IEEE 754规定: 对于32位的浮点数,最高的1位是符号位S,接着的8位是指数E,剩下的23位为有效数字M。
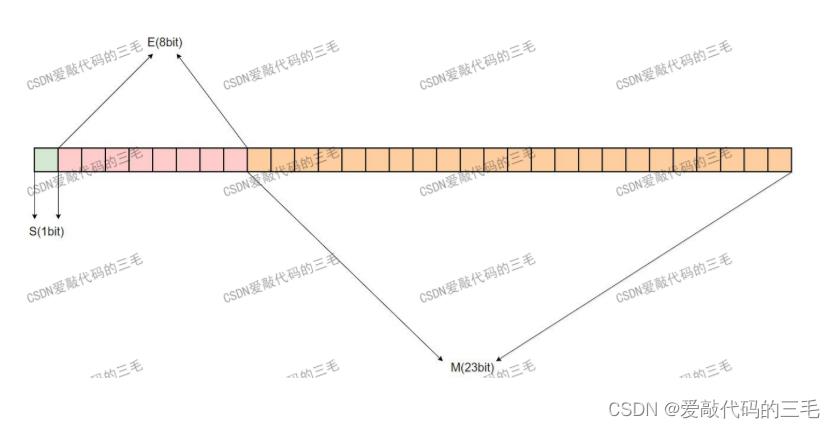
**对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M **
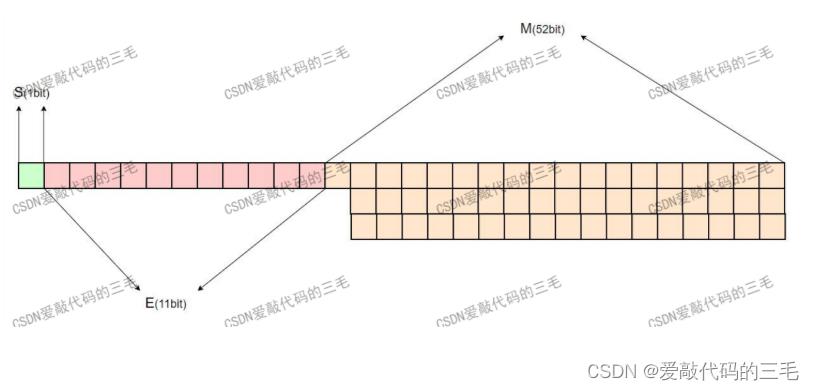
我们发现无论是32为还是64位的浮点数,它能保存的小数点后面的有效数字位都是有限性。所以有些小数在计算机中是没法精确存储的。
比如说3.14
把3.14转换成二进制
3可以转换成 11
而0.14就不好转换成二进制了
0.01转换成十进制就是0.25太大了,0.001转换成二进制就是 0.125,此时不够就得继续凑
再凑个 0.0010001,就变了 0.125+0.0078125=0.1328125
发现和3.14差那么一点点,然后继续凑。
无论怎么凑都是差那么一点点,然后M的有效数字位是有限的更本不够凑
所以有些浮点数在计算机中是没办法精确存储的
IEEE 754对有效数字M和指数E,还有一些特别的规定,前面说过
1
≤
M
<
2
1\\le M<2
1≤M<2,也就是说M可以写成1.XXXXXX的形式,其中小数点右边的标识小数部分
IEEE 754规定,在计算机内部保存M时,默认这个数的第一位都是1,所以可将这个1舍去,只保存小数点右边的.XXXXXX小数部分,比如保存1.101的时候,值保存 101,等到读取的时候,再把舍去的第一位1给加上去。这样做的目的,是为了节省有效数字位,比如32位的单精度浮点数,留给M只有23位,但如果将第一位舍去之后,就相当于可以保存24位有效数字了
对于指数E,情况就比较复杂了
对于指数E,它是一个无符号的整数(unsigned int),这就意味着E如果为8位,它的取值范围就是0~255,如果E为11位,它的取值范围为0 ~ 2047,但是我们知道科学计数法中的E是可以出现负数的。
比如:
我们知道对于一个用科学计数法来表示一个数是有可能出现负数的,比如0.5用二进制来表示就是 0.1,写成科学计数法的形式就是 1.0 ∗ 2 − 1 1.0*2^-1 1.0∗2−1
所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这中间数是1023。比如上面的按个列子,
2
−
1
2^-1
2−1的E是-1,所以保存成32位浮点数的时候,必须保存成
−
1
+
127
=
126
-1+127=126
−1+127=126,所以存进去的就是 0111 1110。同样取出来减去127就好了
然后,指数E从内存中取出还可以分成三种情况:
E不全为0也不全为1
这个时候,浮点数就采用下面的规则表示
也就是指数E减去127(或者1023)得到真实值,再将有效数字M前加上第一位的1
比如6.5的二进制的形式为 110.1,由于规定正数部分必须为1,就得将小数点右移
变成 1.101 ∗ 2 2 1.101*2^2 1.101∗22,它的E为 2 + 127 = 129 2+127=129 2+127=129,表示为 1000 0001
1.101去掉整数部分变成 101,补齐到23位,最后存储到内存中就是
0 10000001 10100000000000000000000
E为全0
这个时候,我们知道我们这E是真实的E+127(或1023)存进去的,如果存进去的E为0那么说明真实的E是-127(或-1023)
我们知道 ( − 1 ) S ∗ M ∗ 2 E (-1)^S * M * 2^E (−1)S∗M∗2E,此时的E是-127就相当于 $\\frac\\pm M2^127 $,是一个 ± ∞ \\pm \\infty ±∞大,无限接近于0的数字
那么此时,浮点数的指数E就直接等于1-127(或者1-1023)即为真实值,有效数字M也不再加上第一位的1了,而是直接还原为
0.XXXXXX的小数,这样做就是为了表示 ± 0 \\pm0 ±0,以及接近于0的很小的数字
E为全1
当E为全1,E的范围是0~255说明我们的真实值是 255 − 127 = 128 255-127=128 以上是关于梦开始的地方 —— C语言数据在内存中的存储(整形+浮点型)的主要内容,如果未能解决你的问题,请参考以下文章