LeetCode 907 子数组的最小值之和[单调栈] HERODING的LeetCode之路

Posted 2022-11-27 HERODING23

解题思路：
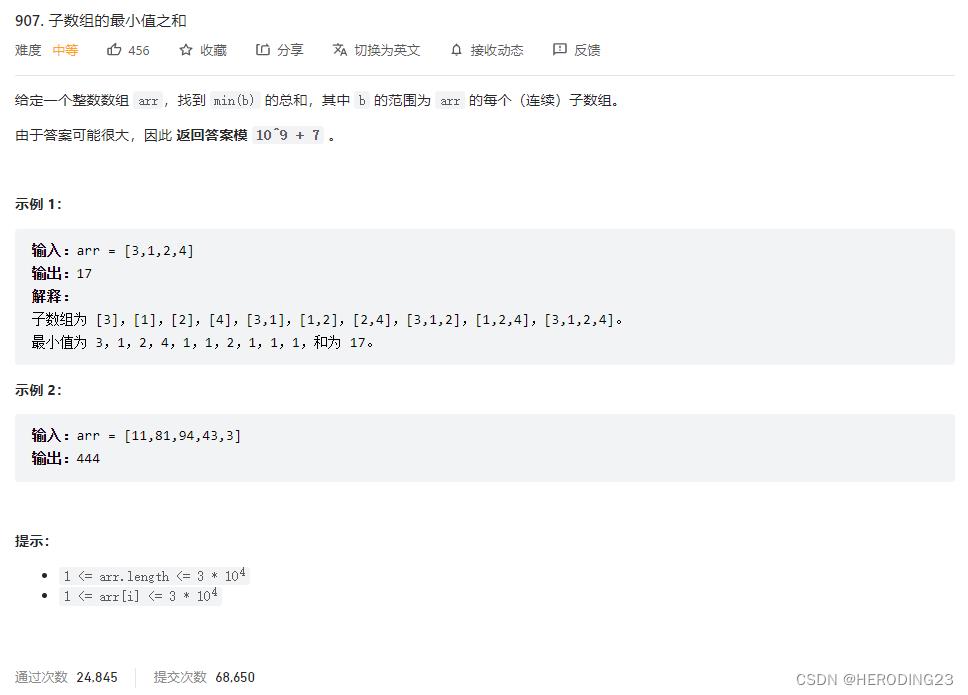
求子数组的最小值之和，如果把所有子数组列出来，找其中的最小值求和，那么一定会超时，因为进行太多重复操作，所以我们只需要固定每个数，求以该数最小值的序列的个数，然后求和这样就快很多，定义栈，定义dp数组存储以当前位置为右界的序列最小值之和，遍历数组，把当前遍历的数作为序列右界，同时要求其为搜索序列中的最小值，那么把栈顶所有大于等于该数的数全部pop()出来，留下左界，以示例2为例，当遍历到43时，栈中留下11，此时序列[81, 94, 43]，[94, 43]，[43]都是以43作为最小元素，那么这几个序列的最小值和为43*(i-left)=43*3，此时，以43为右界的序列还包括有[11, 81, 94, 43]，但是该序列最小值为11，所以还要加上dp[left]，即把左界更小的求和加进去，代码如下：

class Solution 
public:
    const int M = 1e9 + 7;
    int sumSubarrayMins(vector<int>& arr) 
        int n = arr.size();
        stack<int> s;
        vector<int> dp(n, 0);
        int res = 0;
        for(int i = 0; i < n; i ++) 
            int left = -1;
            while(!s.empty() && arr[s.top()] >= arr[i]) 
                s.pop();
            
            if(!s.empty()) left = s.top();
            s.push(i);
            dp[i] = (i - left) * arr[i];
            if(left != -1) dp[i] = (dp[i] + dp[left]) % M;
            res = (res + dp[i]) % M;
        
        return res;
    
;